【表达式求值】

news2024/11/30 2:40:05

目录：

  • 前言
  • 一、有效的括号
    • （一）题目分析
    • （二）整体代码
  • 二、表达式求值
    • （一）题目分析
      • 1.栈的基本操作：
      • 2. 大体思路：
      • 3.具体计算过程：
    • （二）整体代码
  • 总结

前言

在这里插入图片描述
朋友们大家好，前段时间熊猫我学习了栈的相关知识，通过做题发现栈可以解决一些很有价值的事情，比如：表达式求值。
下面我会通过LeetCode上《有效的括号》这个题进行引入，讲解表达式求值的实现，希望能为大家带来帮助。

一、有效的括号

点击跳转LeetCode：有效的括号

题目描述：
给定一个只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串 s ，判断字符串是否有效。
有效字符串需满足：
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。
在这里插入图片描述

（一）题目分析

本题要求我们判断括号是否有效，那么我们需要知道什么形式的括号才是有效的？
1.括号的总数量一定是偶数个，并且左右括号各占一半；
2.左括号必须和与之对应的右括号相结合，既 ‘(’ 必须和 ‘)’ 对应，‘[’ 和 ‘]’ 以及 ‘{’ 和 ‘}’ 亦然；
3.必须先有左括号再有右括号。
通过上面的分析我们可以知道，遇到左括号就入栈，出现右括号就和栈区最后一个左括号进行匹配，匹配上了就出栈，否则就是无效的括号，并且最后栈区是空的。

括号一定是成对出现的

	int sz = strlen(s);
	if (sz % 2 != 0) 
		return false;

遇到左括号就入栈，遇到右括号就出栈

char* arr = (char*)malloc(sz);
	int a = 0; // 记录栈区字符的个数
	for (int i = 0; i < sz; i++)
	{
		switch (s[i])
		{
		case '(':
		case '[':
		case '{':
			arr[a++] = s[i];
			break;
		case ')':
			if (a > 0 && arr[--a] == '(')
				break;
			else
				return false;
				
		case ']':
			if (a > 0 && arr[--a] == '[')
				break;
			else
				return false;
		case '}':
			if (a > 0 && arr[--a] == '{')
				break;
			else
				return false;
		}
	}

最后我们还需要判断栈区是否为空，防止左括号比右括号多

 if(a==0)
	return true;
    else
    return false;

（二）整体代码

示例：

bool isValid(char* s) {
	int sz = strlen(s);
	if (sz % 2 != 0)
		return false;
	char* arr = (char*)malloc(sz);
	int a = 0; // 记录栈区字符的个数
	for (int i = 0; i < sz; i++)
	{
		switch (s[i])
		{
		case '(':
		case '[':
		case '{':
			arr[a++] = s[i];
			break;
		case ')':
			if (a > 0 && arr[--a] == '(')
				break;
			else
				return false;
				
		case ']':
			if (a > 0 && arr[--a] == '[')
				break;
			else
				return false;
		case '}':
			if (a > 0 && arr[--a] == '{')
				break;
			else
				return false;
		}
	}
    if(a==0)
	return true;
    else
    return false;
}

运行实例：
在这里插入图片描述

二、表达式求值

上一个例题我们写的十分简陋，虽然说是用到了栈，不过只是用到了它的思想而没有具体实现出来，下面一个例题熊猫我会直接先把栈区的操作实现出来，让大家真真正正滴了解一下栈的操作（防止大家觉得熊猫我不够专业）。

题目描述：
以字符序列的形式从终端输入语法正确的、不含变量的整数表达式，
我们需要实现对算术四则混合运算表达式的求值。
测试数据：
3*(7-1)；1+2+3+4；88-15；(20+2)(6/2)；6+2*(3+6)。

（一）题目分析

题目要求我们实现对算数四则混合运算表达式的求值，这里我们首先需要注意两点：
1.小括号的优先级最高，我们需要先进行括号里的表达式运算
2.乘法和除法的优先级高于加法和减法

1.栈的基本操作：

#define MALLOC(ty,num) (ty*)malloc(sizeof(ty)*(num))
#define REALLOC(block,ty,num) (ty*)realloc(block,sizeof(ty)*(num));
#define OK 1
#define ERROR 0
#define INITNUM 5	//初始化顺序表长度
#define ADDNUM 3	//之后每次增加的长度
typedef double selemtype;

typedef struct SQStack
{
	selemtype* data;
	int length;
	int maxnum;
}SQS;


void Init(SQS* p)  栈的初始化
{ 
	assert(p);
	p->data = MALLOC(selemtype, INITNUM);
	if (!p->data)
	{
		return;
	}

	p->length = 0;//顺序栈下一个元素的下标
	p->maxnum = INITNUM;
}

void Destroy(SQS* p)  // 栈的销毁
{
	assert(p);

	free(p->data);
	p->length = 0;
	p->maxnum = 0;
}

static int Judge(SQS* p)  // 判断栈区是否已满并扩容
{
	assert(p);
	if (p->length == p->maxnum)//满了
	{
		selemtype* newblock = REALLOC(p->data, selemtype, p->length + ADDNUM);
		if (newblock == NULL)
		{
			return ERROR;
		}

		p->data = newblock;
		p->maxnum = p->length + ADDNUM;
	}
	return OK;
}

void Push(SQS* p, selemtype con)    //  入栈
{
	assert(p);

	Judge(p);

	p->data[p->length] = con;
	p->length++;
}

void Pop(SQS* p)   //  出栈
{
	assert(p);

	p->length--;
}

int JudgeOverflow(SQS* p)   //  判断栈区是否为空
{
	assert(p);

	if (p->length == 0)
	{
		return ERROR;
	}
	else
	{
		return OK;
	}
}

selemtype GetTop(SQS* p)    //   获取栈顶数据
{
	assert(p);

	return p->data[p->length - 1];
}

2. 大体思路：

由于小括号运算优先级最高，所以我们需要先计算括号内再计算括号外；
我们这里可以先判断小括号是否存在，如果没有遇到括号、或者遇到了左括号我们就继续进栈，直到遇到了右括号我们再出栈，
当然，出栈也有限制：
1.出到了左括号就停止出栈，这时一个括号内的表达式就计算结束了
2.如果栈空了就说明这整个表达式就计算结束了，此时我们就已经功德圆满啦（bushi）。

selemtype Expression(char* str)
{
	SQS s;
	Init(&s);

	double con = 0; // 表达式结果
	char* p = NULL; // 

	int i = 0;
	for (i = 0; str[i]; ) // 遍历字符串
	{

		if (isdigit(str[i])) // 判断是数值
		{
		 //  本函数是将字符串转为double类型数据，并且返回转换数据结束时后一个位置的地址，我们将它存放在指针p中
		 //这里不可以直接 push(str[i]);
		 //是为了防止参与运算的数值中有小数、以及不止一位数的数据
			selemtype val = strtod(&str[i], &p); 
			Push(&s, val);

			i = p - str; // 更新下标
		}
		else  // 符号
		{

			if (str[i] != ')')
			{
				Push(&s, str[i]);
			}
			else     // 如果遇到右括号我们就讲括号内的表达式进行一次求值
			{
				con = Evaluation(&s);
				Push(&s, con);   //  求得的值要继续入栈，最后需要再整体进行一次运算
			}

			i++; // 更新下标
		}
	}

	con = Evaluation(&s);    //  整体结果运算

	Destroy(&s);

	return con;
}

经过上面的理想操作，我们就可以得到想要的结果，
为了便于下面运算函数的实现，我们大家可以通过下面的图解来大致了解操作过程。
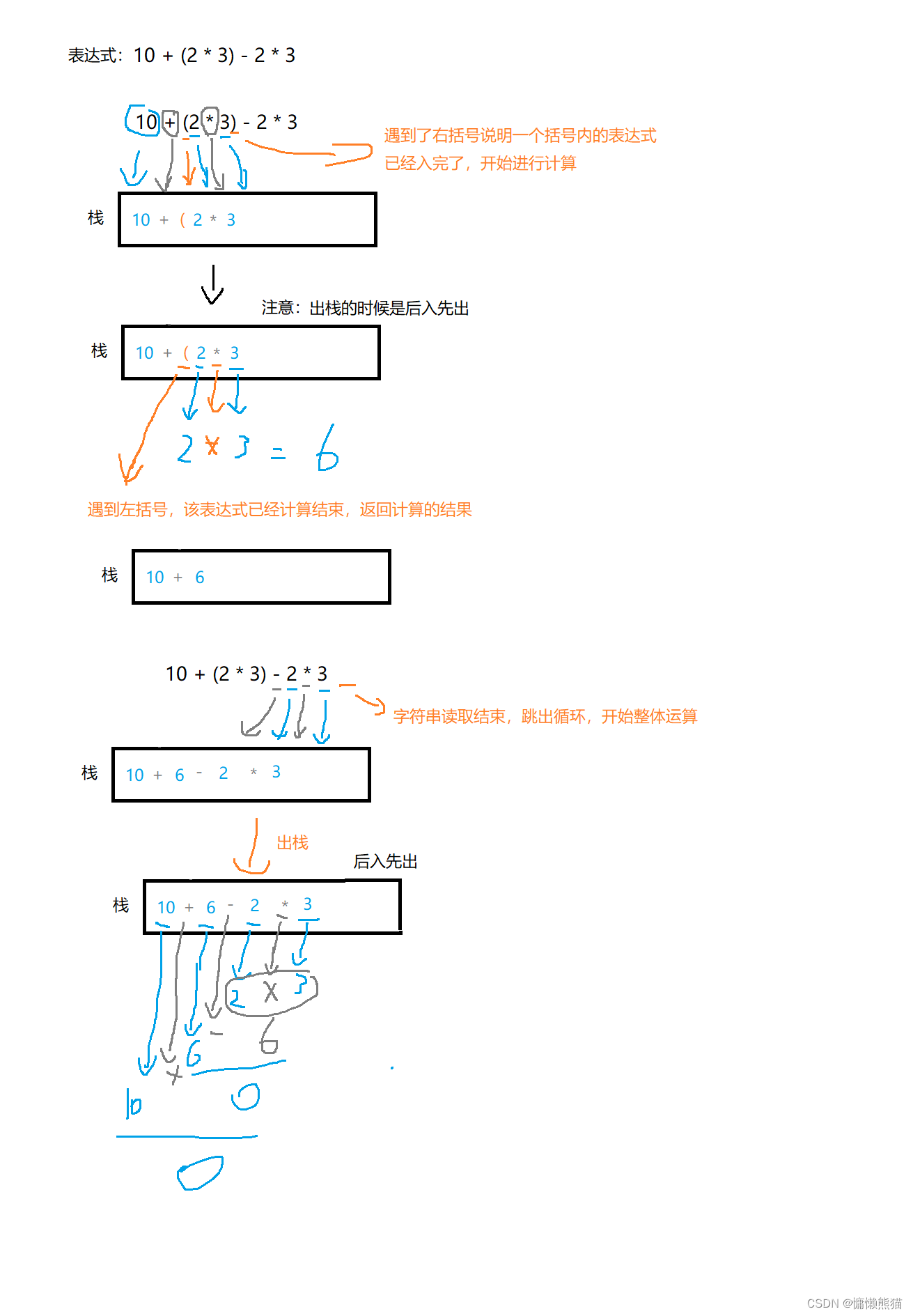
在这里插入图片描述

3.具体计算过程：

这里我们不需要考虑括号，主要考虑的是优先级的问题（还有一些特殊情况）
下面我们先来画图分析一下：
在这里插入图片描述

selemtype Evaluation(SQS* ps)
{
	selemtype con = 0;
	selemtype val1 = GetTop(ps); // 数值
	Pop(ps);
	selemtype val2 = 0;

	while (JudgeOverflow(ps)) // 栈为空就退出
	{

		switch ((char)GetTop(ps))
		{
		case'+':
		{
			Pop(ps); // 将 '+' 出栈

			val2 = GetTop(ps);
			Pop(ps);

			con += val1;
			val1 = val2;

		}
		break;

		case '-':
		{
			Pop(ps);

			if (!JudgeOverflow(ps))  //  特殊1.这个地方是要避免第一个数是负数
			{
				con -= val1;
				return con;
			}

			val2 = GetTop(ps);
			Pop(ps);

			con -= val1;
			val1 = val2;

		}
		break;

		case '*':
		{
			Pop(ps);

			val1 *= GetTop(ps);
			Pop(ps);
		}
		break;

		case '/':
		{
			Pop(ps);
			val2 = GetTop(ps);
			Pop(ps);
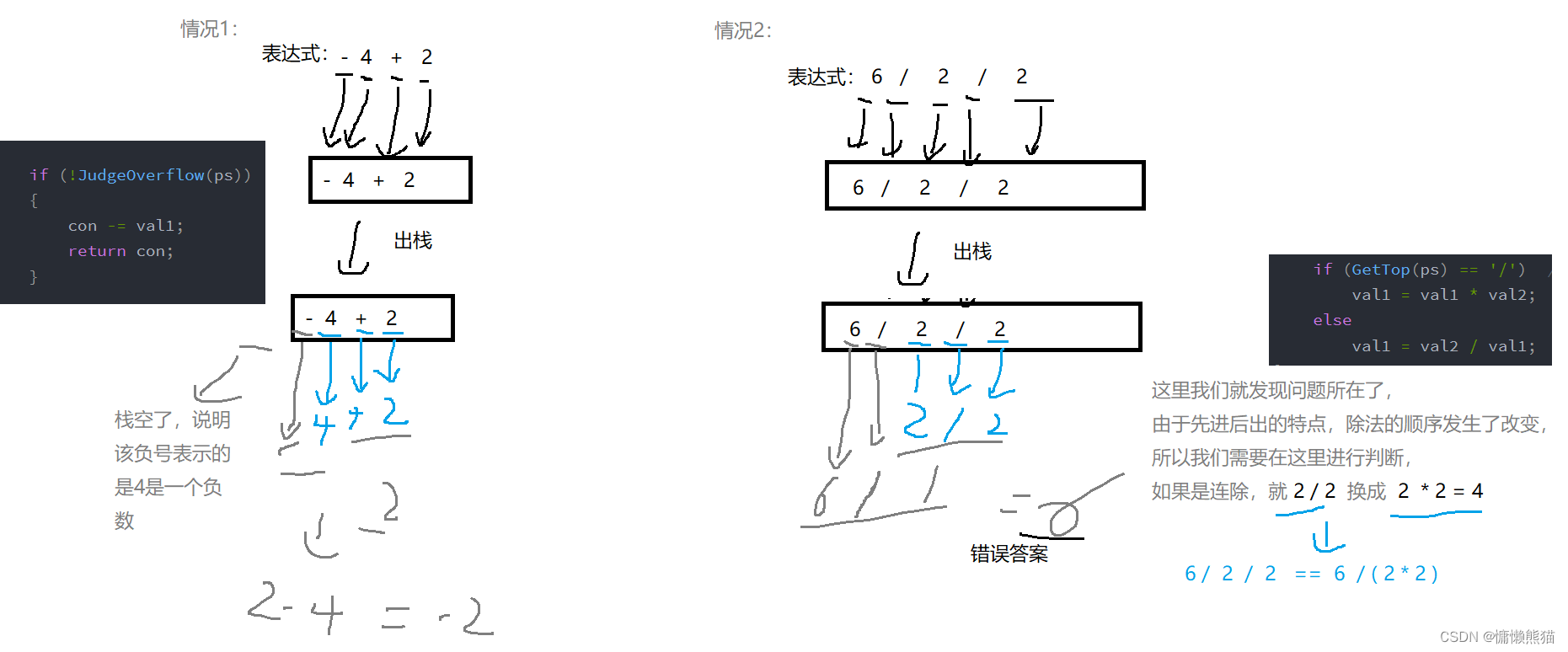
			if (GetTop(ps) == '/')  //  特殊2：出栈是后进先出的，因此如果出现连除情况需要特殊处理
				val1 = val1 * val2;
			else
				val1 = val2 / val1;
		}
		break;

		case '(':
			Pop(ps);
			goto end;
		}
	}

end:
	con += val1;
	return con;

}

两种特殊情况：
在这里插入图片描述

（二）整体代码

示例：

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<ctype.h>
#include<assert.h>

#define MALLOC(ty,num) (ty*)malloc(sizeof(ty)*(num))
#define REALLOC(block,ty,num) (ty*)realloc(block,sizeof(ty)*(num));
#define OK 1
#define ERROR 0
#define INITNUM 5	//初始化顺序表长度
#define ADDNUM 3	//之后每次增加的长度
typedef double selemtype;

typedef struct SQStack
{
	selemtype* data;
	int length;
	int maxnum;
}SQS;


void Init(SQS* p)
{
	assert(p);
	p->data = MALLOC(selemtype, INITNUM);
	if (!p->data)
	{
		return;
	}

	p->length = 0;//顺序栈下一个元素的下标
	p->maxnum = INITNUM;
}

void Destroy(SQS* p)
{
	assert(p);

	free(p->data);
	p->length = 0;
	p->maxnum = 0;
}

static int Judge(SQS* p)
{
	assert(p);
	if (p->length == p->maxnum)//满了
	{
		selemtype* newblock = REALLOC(p->data, selemtype, p->length + ADDNUM);
		if (newblock == NULL)
		{
			return ERROR;
		}

		p->data = newblock;
		p->maxnum = p->length + ADDNUM;
	}
	return OK;
}

//入栈
void Push(SQS* p, selemtype con)
{
	assert(p);

	Judge(p);

	p->data[p->length] = con;
	p->length++;

}

void Pop(SQS* p)
{
	assert(p);

	p->length--;
}

int JudgeOverflow(SQS* p)
{
	assert(p);

	if (p->length == 0)
	{
		return ERROR;
	}
	else
	{
		return OK;
	}
}

selemtype GetTop(SQS* p)
{
	assert(p);

	return p->data[p->length - 1];
}

selemtype Evaluation(SQS* ps)
{
	selemtype con = 0;
	selemtype val1 = GetTop(ps); // 数值
	Pop(ps);
	selemtype val2 = 0;

	while (JudgeOverflow(ps))
	{

		switch ((char)GetTop(ps))
		{
		case'+':
		{
			Pop(ps); // 将 '+' 出栈

			val2 = GetTop(ps);
			Pop(ps);

			con += val1;
			val1 = val2;

		}
		break;

		case '-':
		{
			Pop(ps);

			if (!JudgeOverflow(ps))
			{
				con -= val1;
				return con;
			}

			val2 = GetTop(ps);
			Pop(ps);

			con -= val1;
			val1 = val2;

		}
		break;

		case '*':
		{
			Pop(ps);

			val1 *= GetTop(ps);
			Pop(ps);
		}
		break;

		case '/':
		{
			Pop(ps);
			val2 = GetTop(ps);
			Pop(ps);
			if (GetTop(ps) == '/')
				val1 = val1 * val2;
			else
				val1 = val2 / val1;
		}
		break;

		case '(':
			Pop(ps);
			goto end;
		}
	}

end:
	con += val1;
	return con;

}

selemtype Expression(char* str)
{
	SQS s;
	Init(&s);

	double con = 0; // 表达式结果
	char* p = NULL; // 

	int i = 0;
	for (i = 0; str[i]; ) // 遍历字符串
	{

		if (isdigit(str[i])) // 数值
		{
			selemtype val = strtod(&str[i], &p);
			Push(&s, val);

			i = p - str; // 更新下标
		}
		else  // 符号
		{

			if (str[i] != ')')
			{
				Push(&s, str[i]);
			}
			else
			{
				con = Evaluation(&s);
				Push(&s, con);
			}

			i++; // 更新下标
		}
	}

	con = Evaluation(&s);

	Destroy(&s);

	return con;
}

int main()
{
	while (1)
	{
		printf("请输入表达式：");
		char str[100] = { 0 };
		scanf("%s", str);

		selemtype con = 0;//表达式结果
		con = Expression(str);
		printf("表达式结果为：%.2lf\n\n", con);
	}
	return 0;
}

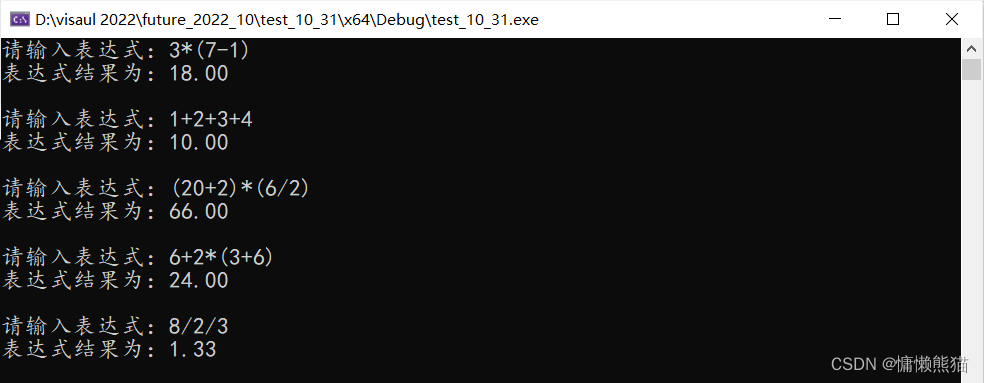
运行实例：

在这里插入图片描述

总结

以上就是表达式求值的全部内容，熊猫这边建议大家在学习的过程中可以尝试着做一些有趣的东西，这样不仅能够提高自己的学习积极性，对自己的实力也能做到很好的打磨，何乐而不为呢~。
那么今天就讲解到这里，如果有什么疑问或者建议都可以在评论区留言，感谢大家对在这里插入图片描述的支持。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/3175.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【代码随想录】二刷-哈希表

【代码随想录】二刷-哈希表

哈希表 《代码随想录》 哈希表一般用来快速查找某个元素是否在一个集合中。如果使用枚举的话时间复杂度为O(n)&#xff0c;而使用哈希表只O(1)就可以做到。——元素查询。 242.有效的字母异位词 使用unordered_map // 时间复杂度 O(n) // 空间复杂度 O(n) class Solution { pub…
阅读更多...
嵌入式分享合集94

嵌入式分享合集94

一、单片机硬件电路设计 减少后级电源对前级的影响&#xff0c;防止电源正负接反烧坏后级电路&#xff0c;防止电源关电时电流倒灌&#xff0c;但经过二极管有0.4V左右压降&#xff0c;需要考虑经过0.4V降压后会不会低于后级电路的正常工作电压。 一、按键电路 R1上拉电阻&…
阅读更多...
用C语言开发入门游戏FlappyBird

用C语言开发入门游戏FlappyBird

前言 《flappy bird》是一款由来自越南的独立游戏开发者Dong Nguyen所开发的作品&#xff0c;游戏于2013年5月24日上线&#xff0c;并在2014年2月突然暴红。2014年2月&#xff0c;《Flappy Bird》被开发者本人从苹果及谷歌应用商店撤下。2014年8月份正式回归APP Store&#xf…
阅读更多...
java从零开始系统性学习完整笔记（一）

java从零开始系统性学习完整笔记（一）

java从零开始系统性学习完整超全资源笔记(还在更新中&#xff09; 前言 资源来自&#xff1a;王汉远java基础&#xff0c; B站视频&#xff1a; https://www.bilibili.com/video/BV1b4411g7bj/?spm_id_from333.1007.top_right_bar_window_custom_collection.content.click&a…
阅读更多...
渗透测试之分享常用工具、插件和脚本（干货）

渗透测试之分享常用工具、插件和脚本（干货）

BRUP插件&#xff1a; 漏洞挖掘插件&#xff1a;Autorize、CSRF Token Tracker、XSS Validator、Turbo Intruder 辅助插件&#xff1a;HaE、sqlmap4brup、hackbar、Software Vulnerability Scanner 浏览器插件&#xff1a; wappalyzer、MySSL、Cookie Editor 脚本&#xff1a; …
阅读更多...
Vue学习：vue生命周期

Vue学习：vue生命周期

Vue实例有一个完整的生命周期&#xff0c;也就是从开始创建、初始化数据、编译模板、挂载Dom、渲染→更新→渲染、卸载等一系列过程&#xff0c;我们称这是Vue的生命周期。通俗说就是Vue实例从创建到销毁的过程&#xff0c;就是生命周期。生命周期又称为生命周期回调函数&#…
阅读更多...
水果叠叠乐

水果叠叠乐

水果叠叠乐 介绍 消消乐是一款益智类小游戏&#xff0c;最近比较火爆的一种是立体叠叠乐式的&#xff0c;然后小蓝也想开发一个自己练练手&#xff0c;给它起名叫“水果叠叠乐”。 准备 本题已经内置了初始代码&#xff0c;打开实验环境&#xff0c;目录结构如下&#xff1…
阅读更多...
OSPF高级配置——学习OSPF路由协议的高级应用

OSPF高级配置——学习OSPF路由协议的高级应用

作者简介&#xff1a;一名在校云计算网络运维学生、每天分享网络运维的学习经验、和学习笔记。 座右铭&#xff1a;低头赶路&#xff0c;敬事如仪 个人主页&#xff1a;网络豆的主页​​​​​​ 目录 前言 一.路由重分发及配置 1.路由重分发概述 2.理解路由重分发 3.路…
阅读更多...
【HMS Core】华为分析SDK如何申请数据导出功能？

【HMS Core】华为分析SDK如何申请数据导出功能？

1、问题描述 项目中集成了华为分析SDK&#xff0c;现在有一个需求&#xff0c;想要申请数据导出功能&#xff0c;申请页面提示数据导出功能目前仅对部分邀请伙伴开放&#xff0c;需要通过在线提单的方式申请开通此功能&#xff0c;那么具体该如何操作呢&#xff1f; 2、解决方…
阅读更多...
校园跑腿微信小程序,校园跑腿小程序,微信小程序跑腿系统毕设作品

校园跑腿微信小程序,校园跑腿小程序,微信小程序跑腿系统毕设作品

项目背景和意义 目的&#xff1a;本课题主要目标是设计并能够实现一个基于微信校园跑腿小程序系统&#xff0c;前台用户使用小程序发布跑腿任何和接跑腿任务&#xff0c;后台管理使用基于PHPMySql的B/S架构&#xff1b;通过后台管理跑腿的用户、查看跑腿信息和对应订单。 意义…
阅读更多...
C++ Reference: Standard C++ Library reference: C Library: cwchar: wcstoll

C++ Reference: Standard C++ Library reference: C Library: cwchar: wcstoll

C官网参考链接&#xff1a;https://cplusplus.com/reference/cwchar/wcstoll/ 函数 <cwchar> wcstoll long long int strtoll (const wchar_t* str, wchar_t** endptr, int base); 将宽字符串转换为long long整数 解析C宽字符串str&#xff0c;将其内容解释为指定base的…
阅读更多...
高级FPGA设计结构实现和优化_(六)静态时序分析

高级FPGA设计结构实现和优化_(六)静态时序分析

高级FPGA设计结构实现和优化_静态时序分析标准分析锁存器组合反馈标准分析 静态时序分析(STA)指的是在一个设计中与一组约束有关的所有时序路径的综合性分析&#xff0c;为了确定一个设计是否是“时序一致的”。由FPGA设计者遇到的基本路径是输入到触发器、触发器到触发器、触发…
阅读更多...
MySQL进阶一 一条select语句的执行流程

MySQL进阶一 一条select语句的执行流程

文章目录前言MySQL的执行流程第一步&#xff1a;连接器第二步&#xff1a;查询缓存第三步&#xff1a;解析SQL第四步&#xff1a;执行 SQL预处理器优化器执行器主键索引查询全表扫描索引下推总结前言 有一位同志问我为什么很久没更新了&#xff0c;因为前一个礼拜在复盘JavaSE…
阅读更多...
【详解】手撕 一维、二维、三维差分数组原理（附图解，模板，例题分析）

【详解】手撕 一维、二维、三维差分数组原理（附图解，模板，例题分析）

【差分专题】 引言 ​ 差分是一种处理数据巧妙而简单的方法&#xff0c;可以应用于区间修改和询问问题。例如&#xff0c;将给定的数据集合 A 分成很多区间&#xff0c;并对这些区间进行很多次操作&#xff0c;每次都是对某段区间内的所有元素做相同的加减操作&#xff0c;此…
阅读更多...
YOLOv7学习笔记（一）——概述+环境+训练

YOLOv7学习笔记（一）——概述+环境+训练

一、环境安装测试 1、创建环境conda create -n yolo python3.7conda activate yolo2、安装pytorchconda install pytorch torchvision cudatoolkit11.3 -c pytorch11.3为cuda版本号3、克隆yolov5git clone https://github.com/WongKinYiu/yolov7 # clonecd yolov7pip install…
阅读更多...
真的要转到云IDE了吗？VS Code的开源IDE

真的要转到云IDE了吗？VS Code的开源IDE

云IDE产品介绍 云IDE使用教程 免费使用地址&#xff1a;点击【云IDE】&#xff0c;即可开始创建工作空间啦~ 前言 CSDN最新产品【云IDE】来啦&#xff01;【云IDE】将为各位技术er一键秒级构建云开发环境&#xff0c;提升开发效率&#xff01; 1. 什么是IDE&#xff1f; 做…
阅读更多...
PyTorch 1.13 正式发布：CUDA 升级、集成多个库、M1 芯片支持

PyTorch 1.13 正式发布：CUDA 升级、集成多个库、M1 芯片支持

内容导读&#xff1a;近日&#xff0c;PyTorch 团队在官方博客宣布 Pytorch 1.13 发布。本文将详细围绕新版本的 4 大亮点展开介绍。 据官方介绍&#xff0c;PyTorch 1.13 中包括了 BetterTransformer 的稳定版&#xff0c;且不再支持 CUDA 10.2 及 11.3&#xff0c;并完成了向…
阅读更多...
大数据项目之电商数仓、业务数据介绍、业务数据模拟、生成业务数据、业务数据建模

大数据项目之电商数仓、业务数据介绍、业务数据模拟、生成业务数据、业务数据建模

文章目录6. 业务数据介绍6.5 业务数据模拟6.5.1 连接MySQL6.5.2 建表语句6.5.3 生成业务数据6.5.3.1 在hadoop102的/opt/module/目录下创建db_log文件夹6.5.3.2 把gmall2020-mock-db-2021-11-14.jar和application.properties上传到hadoop102的/opt/module/db_log路径上6.5.3.3 …
阅读更多...
[CSS]常见布局技巧

[CSS]常见布局技巧

前言 系列文章目录&#xff1a; [目录]HTML CSS JS 根据视频和PPT整理视频及对应资料&#xff1a;HTML CSS 老师笔记&#xff1a; https://gitee.com/xiaoqiang001/html_css_material.git视频&#xff1a;黑马程序员pink老师前端入门教程&#xff0c;零基础必看的h5(html5)css3…
阅读更多...
榛子树搜索算法（Hazelnut tree search algorithm，HTS）附matlab代码

榛子树搜索算法（Hazelnut tree search algorithm，HTS）附matlab代码

✅作者简介&#xff1a;热爱科研的Matlab仿真开发者&#xff0c;修心和技术同步精进&#xff0c;matlab项目合作可私信。 &#x1f34e;个人主页&#xff1a;Matlab科研工作室 &#x1f34a;个人信条&#xff1a;格物致知。 更多Matlab仿真内容点击&#x1f447; 智能优化算法 …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023