目录
1. 介绍
2. 分水岭算法的实现
距离变换
连接连通分量
3. 代码
1. 介绍
图像是由x,y表示的,如果将灰度值也考虑进去的话,那么一幅图像需要一个三维的空间去表示。

这样就可以把x,y轴比作大地,将灰度值的z轴比作地面上的坡度。
因为图像的灰度值是不均匀的,那么也意味着这个地面也是坑坑洼洼的。那么试想一下,下雨的时候,由于地面是不平坦的,雨水会顺着高的地面流向地处。必然会导致有的地方堆满了水,有的地方由于地势较陡,没有雨水

分水岭算法就是利用这种“地形学”,或者说灰度值的不均匀对图像进行分割。
在这种将图像类比成地形的方法里,主要考虑三种点:
- 属于区域极小值的点
- 水滴所在位置的点,如果把水滴放在任意位置,水滴必然流向某个极小值
- 水等概率的流向不止一个极小值的点
在这里,如果某个区域是极小值,且满足第二个条件的点集称为汇水盆地或者分水岭
满足第三个条件的点形成地形表面的线,称为分界线
分水岭算法实现的思路是:
找到一些初始点,然后对这些点集进行灌水。随着水位的上升,不同区域的水会开始融合。为了阻止这种现象,在这些融合处建立拦水坝,这样拦水坝就把图像进行了分割
初始点的选择需要用到距离变换
2. 分水岭算法的实现
首先尝试对下面的算法进行分水岭算法的分割

这里读取的是彩色图像,因为最后的 watershed 函数需要传入彩色图像

这里对图像进行阈值处理的结果为

阈值处理发现,这里硬币内部出现了孔洞,在背景上也出现了白色的噪声点
因为开运算可以消除白色的噪声,而闭运算可以消除内部的孔洞,所以这里采用形态学的方法进行处理。具体的可以参考:灰度级形态学 - 灰度开运算和灰度闭运算


接下来,通过膨胀,将前景扩大,这样就可以确定哪些是背景,哪些是前景


这一步主要为了确定真正的前景区域
距离变换
接下来,通过距离变换可以找到这些硬币近似的中心点。先展示下效果,在做讲解

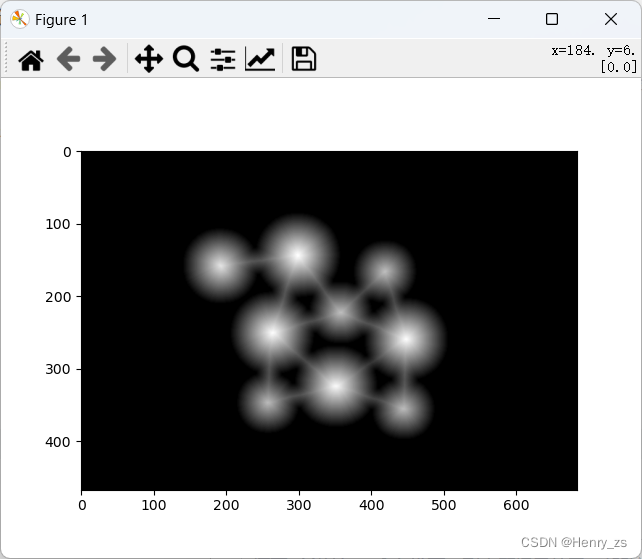
因为数据类型的原因,这种用 matplotlib 展示。这里距离变换会计算前景像素点到周围最近背景像素点的距离,所以这里像素点越亮,距离背景越远。并且输入图像必须是个二值图像

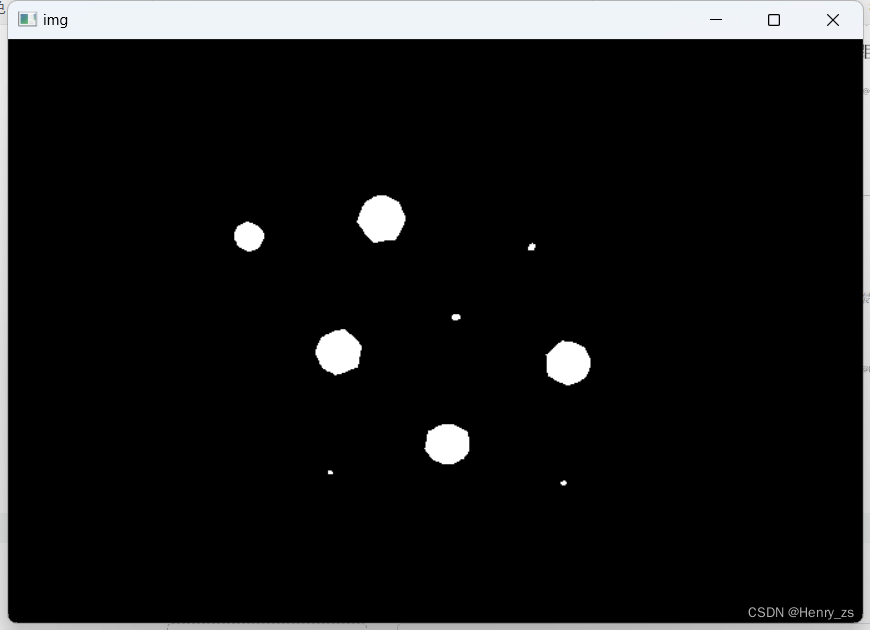
然后,获取距离变换中距离背景远处的点,这些点就是我们分水岭算法的初始点
因为现在的前景区域一定是硬币的位置

unknown 是不确定区域,或者说,这里是有分线线的地方
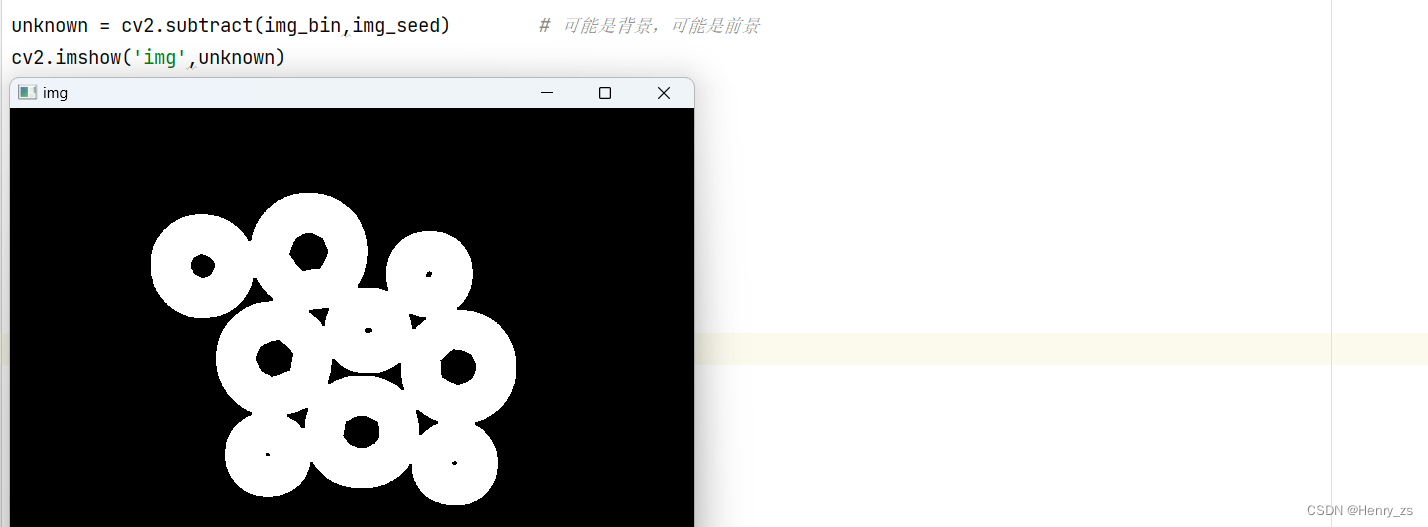
连接连通分量
它会把将背景标记为 0,其他的对象使用从 1 开始的正整数标记

这样,分水岭算法会从每个标记的位置开始注水,除了0未知区域。这样水位升高的时候,不同区域的水就会在未知区域相遇,这样分界线就被找出来了

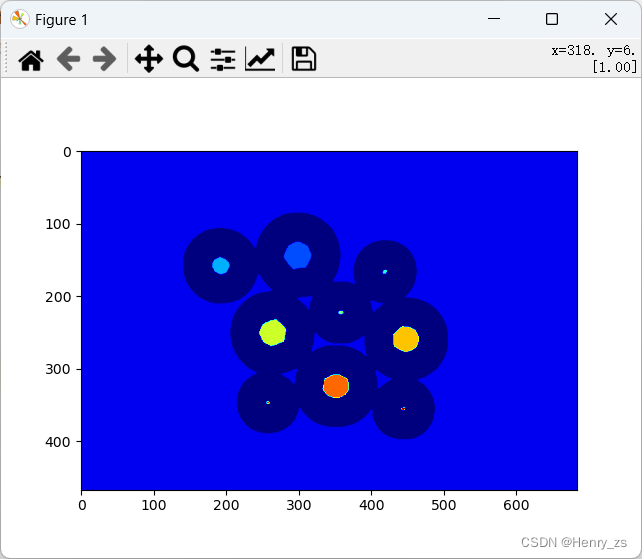
分水岭算法会将不同区域之间的边界设置为 -1
watershed的结果中只有-1,0,1,2这样的数

分水岭算法的结果:
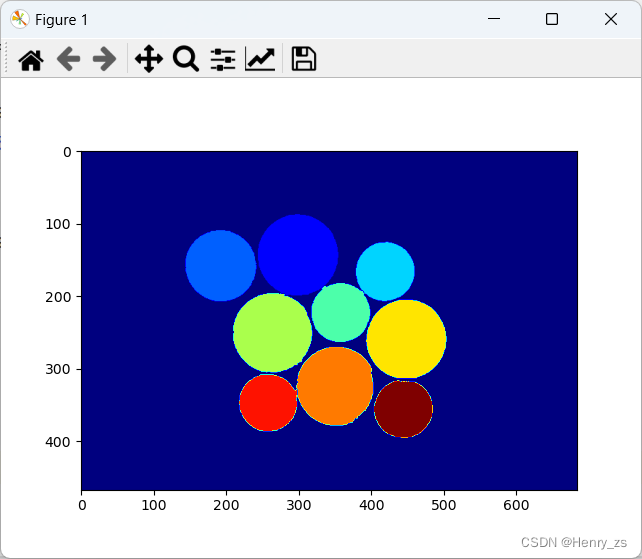
分割的结果:

3. 代码
import cv2
import numpy as np
import matplotlib.pyplot as plt
src = cv2.imread('./img.png') # 彩色图像
img = src.copy()
img = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY) # 转为灰度图像
ret, img_bin = cv2.threshold(img, 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU) # 阈值处理
kernel = cv2.getStructuringElement(cv2.MORPH_RECT,(3,3)) # 获取结构元
img_close = cv2.morphologyEx(img_bin, cv2.MORPH_CLOSE, kernel, iterations=3) # 闭运算填充内部的孔洞
img_open = cv2.morphologyEx(img_close, cv2.MORPH_OPEN, kernel, iterations=2) # 开运算消除白色噪声
img_bin = cv2.dilate(img_open, kernel, iterations=2) # 膨胀确定前景和背景
dist_transform = cv2.distanceTransform(img_bin, cv2.DIST_L2, 5) # 距离变换
ret, img_seed = cv2.threshold(dist_transform, 0.7 * dist_transform.max(), 255, cv2.THRESH_BINARY) # 获取距离背景最远的点
img_seed = np.uint8(img_seed) # 转为图像的形式
unknown = cv2.subtract(img_bin,img_seed) # 可能是背景,可能是前景
ret, markers = cv2.connectedComponents(img_seed) # 连接连通分量
markers = markers + 1 # 确保背景是1不是0
markers[unknown == 255] = 0 # 未知区域标记为0
markers = cv2.watershed(src, markers) # 分水岭算法
src[markers == -1] = [255,0,0] # 将边界找出
plt.imshow(np.abs(markers),cmap = 'jet') # 分水岭算法结果
plt.show()
cv2.imshow('img',src) # 分割结果
cv2.waitKey()
cv2.destroyAllWindows()