数据结构 | 栈和队列

news2024/9/19 11:05:38

…

📘📖📃本文已收录至：数据结构 | C语言
更多知识尽在此专栏中!
道阻且长，行则将至
欢迎标头

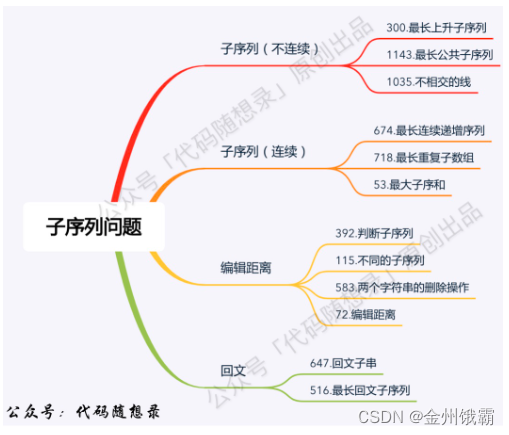
文章目录

  • 📘前言
  • 📘正文
    • 📖栈
      • 📃结构
      • 📃初始化
      • 📃销毁
      • 📃入栈、出栈
      • 📃查看栈顶元素
      • 📃查看栈内有效元素
      • 📃判断栈是否为空
    • 📖队列
      • 📃结构
      • 📃初始化
      • 📃销毁
      • 📃入队、出队
      • 📃查看队头、队尾元素
      • 📃查看队内有效元素
      • 📃判断队是否为空
    • 📖源码区
      • 📃栈
      • 📃队列
    • 📖相关OJ试题推荐
  • 📘总结

📘前言

栈（Stack）又名堆栈，它是一种运算受限的线性表，限定仅在表尾进行插入和删除操作的线性表。队列（Queue）也是一种特殊的线性表，特殊之处在于它只允许在表的前端（Front）进行删除操作，而在表的后端（Rear）进行插入操作，和栈一样，队列 的部分操作也会受到限制。栈 的特点是 先进后出（FILO），队列 则是 先进先出（FIFO），本文将会通过顺序存储的方式模拟实现 栈，以及链式存储的方式模拟实现 队列，两种数据结构都比较简单，一起来看看吧！
云想衣裳花想容

📘正文

📖栈

首先介绍 栈 的实现，栈 非常适合通过 顺序表 来模拟实现，因为 顺序表 尾插、尾删的复杂度是O(1)，并且 栈 的插入、删除都是在 栈顶 完成的，因此我们可以去除 顺序表 的部分功能，这样就可以得到一个 栈
顺序表实现栈

有人将栈形象的比作弹匣，装弹是在入栈，而将子弹射出则是在出栈，显然最先进入弹匣的子弹，将会在最后才被射出，准备的动图发不出来，可以自行百度查看

📃结构

既然可以通过 顺序表 实现 栈 ，那么 栈 的结构自然就和 顺序表 差不多了，都有一个 负责指向存储数据的指针 ，一个 下标(栈顶) 和 容量 ，因为 顺序表要求空间必须是连续的，因此后续需要进行动态内存开辟，而容量是不能少的

typedef int STDataType;	//栈的元素类型

typedef struct StackInfo
{
	STDataType* data;	//数据
	int top;	//栈顶
	int capacity;	//容量
}Stack;

结构展示

📃初始化

初始化需要把 指针 data 置空，栈顶值 top 和 容量值 capacity 归0

  • 当然这里的栈顶也可以置为-1，当我们取栈顶元素时，取的就是当前栈顶处的元素
  • 如果是归0，那么取的就是栈顶-1处的元素
  • 推荐归0，因为在后续操作中比较省事
void StackDestroy(Stack* ps)	//栈的销毁
{
	assert(ps);


	//只有为栈开辟空间了，才能正常销毁
	if (ps->data)
	{
		free(ps->data);
		ps->data = NULL;
		ps->top = ps->capacity = 0;
	}
}

📃销毁

销毁 栈 需要明白一点：是否可以销毁 ，因为可能会出现不插入元素的情况下，结束程序，此时如果继续执行销毁，就会发生空指针的解引用情况


void StackDestroy(Stack* ps)	//栈的销毁
{
	assert(ps);


	//只有为栈开辟空间了，才能正常销毁
	if (ps->data)
	{
		free(ps->data);
		ps->data = NULL;
		ps->top = ps->capacity = 0;
	}
}

销毁栈

📃入栈、出栈

顺序 栈 的 入栈、出栈 很简单，可以放一起介绍

  • 入栈
    • 确保有空间可以使用，因此需要借助扩容程序段
    • 直接将目标值插入到栈顶处
    • 最后栈顶+1，此时的栈顶代表着 栈 中的有效元素个数
void StackPush(Stack* ps, STDataType x)	//入栈
{
	assert(ps);

	//判断栈是否满
	if (ps->top == ps->capacity)
	{
		int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;	//二倍扩容
		STDataType* tmp = (STDataType*)realloc(ps->data, sizeof(STDataType) * newCapacity);
		//如果扩容失败，需要报错并结束程序
		if (tmp == NULL)
		{
			perror("realloc :: fail");
			exit(-1);
		}

		ps->data = tmp;
		ps->capacity = newCapacity;
	}

	//入栈，就是在栈顶处放入元素，然后栈顶+1
	ps->data[ps->top] = x;
	ps->top++;
}

入栈

  • 出栈
    • 出栈需要确保 栈 内有元素可出
    • 如果 栈 为空，是不能执行出栈的
    • 出栈不需要将元素抹掉，直接栈顶-1，无法访问到此元素就行了
void StackPop(Stack* ps)	//出栈
{
	assert(ps);
	assert(ps->top > 0);	//有元素才能出栈

	//出栈，直接栈顶-1
	ps->top--;
}

出栈

📃查看栈顶元素

前面说过，栈顶值 top-1 代表的就是当前栈顶元素，前提是有元素存在，因此这个函数就很简单了，直接先判断 栈 是否为空，如果不为空，返回 栈顶-1 处的元素值就行了

STDataType StackTop(Stack* ps)	//查看栈顶元素
{
	assert(ps);
	assert(ps->top > 0);	//有元素才能看

	//栈顶元素，在栈顶-1处，因为栈顶是从0开始的
	return ps->data[ps->top - 1];
}

查看栈顶元素

📃查看栈内有效元素

所谓栈内有效元素，就是顺序 栈 的长度，也就是 栈顶值 top ，此时就体现出 栈顶值 从0开始的好处了，做什么都很方便，比如这里，直接返回 栈顶值 就行了

int StackSize(Stack* ps)	//查看栈的有效元素个数
{
	assert(ps);

	//栈的大小就是当前栈的有效元素个数
	return ps->top;
}

栈内有效元素

📃判断栈是否为空

判断栈是否为空，太简单了，一行代码解决

  • 返回的是布尔值，需要引头文件 stdbool.h
  • 因为判断式返回值是布尔类型
    • 如果栈顶值为0，说明栈空，判断式为真，返回 true
    • 否则说明栈不空。判断式为假，返回 false
bool StackEmpty(Stack* ps)	//判断栈是否为空
{
	assert(ps);

	//栈顶为0.说明栈空
	return ps->top == 0;
}

顺序 栈 也就这点东西，我愿称之为顺序表青春版，所有源码放在gitee上了，可以跳转到源码区传送过去

下面是程序运行图(测试的时候手速太快了，所以有的地方可能看不太清楚)
这是一张动图，时长56秒
栈运行的动图

📖队列

队列 的特点是先进先出，主要功能是头部删除和尾部插入，因为队列比较特殊，如果采用 顺序表 的形式实现的话，容易出现 假溢出 问题（后续解决 循环队列 问题会用 顺序表 模拟实现），因此我们这里采取 链表 的形式模拟实现 队列

分析得出队列的 需求 如下

  • 单链表就足够了，多加一个队尾指针，可以有效避免效率问题
  • 哨兵位（可要可不要），因为待会实现时，是结构体嵌套结构体的形式
  • 使用非循环的链表，没必要使用双向带头循环链表（小题大做）

结论

  • 最简单的单链表就可以实现
  • 因为有队头、队尾两个指针，因此需要使用结构体嵌套的方式
    链表实现队列

📃结构

单链表 最大的缺陷就是不好找尾，为此我们直接通过结构体嵌套定义的方式，定义 队头指针 front 、队尾指针 rear 和 队列长度 size，这样一来，所有涉及队列的操作，都是在以 O(1) 效率执行，灰常高效，就是比较难理解

帮助理解

  • 假设队列中的节点是一个个链接的小球
  • 存在一个大外壳装着这些小球
  • 并且有两个警卫分别守着球头和球尾，还有一个秘书帮忙记录球数
  • 当然它们的作用是为了更好的管理小球
  • 显然，front 和 rear 就是两个警卫，而 size 是秘书
typedef int QListDataType;	//队列的数据类型

//这是队列中，单个节点的信息
typedef struct QListNode
{
	QListDataType data;
	struct QListNode* next;
}QNode;

//这是整个队列的信息，包含了队头和队尾两个指针
typedef struct QueueNode
{
	QNode* front;	//队头指针
	QNode* rear;	//队尾指针
	size_t size;	//队列长度
}Queue;

队列的结构

📃初始化

队列 的初始化很直接，把 队尾、队头指针 置空，长度 置0就行了

void QueueInit(Queue* pq)	//队列的初始化
{
	assert(pq);

	//初始化状态：队头、队尾指针都指向空，队列大小为0
	pq->front = pq->rear = NULL;
	pq->size = 0;
}

📃销毁

队列 销毁原理，和 单链表 的销毁差不多，需要借助一个 临时指针 cur ，指向当前队头，然后 队头指针 front 移向下一个位置，销毁 临时指针 cur ，如此循环，直到 临时指针 cur 指向 NULL ，此时整个 队列 都会被销毁

  • 队列 不需要像 栈 那样做特殊处理，因为当队空时，cur 一开始就为空，循环是进不去的
  • 当然销毁后，两个指针都要置空，size 也要归零
void QueueDestroy(Queue* pq)	//队列的销毁
{
	assert(pq);

	//销毁思路：利用临时指针进行销毁
	QNode* cur = pq->front;
	while (cur)
	{
		QNode* tmp = cur->next;
		free(cur);
		cur = tmp;
	}

	pq->front = pq->rear = NULL;
	pq->size = 0;
}

队列的销毁

📃入队、出队

有了 队头、队尾 两个指针，入队、出队就很简单了，直接易如反掌

入队

  • 即单链表的尾插
  • 买一个新节点，存放目标值，将 队尾指针 与新节点链接起来
    • 注意：如果是第一次入队，直接赋值，而不是链接
  • 更新 队尾指针 ，队尾指针 变成了新节点
  • 队列长度 + 1
void QueuePush(Queue* pq, QListDataType x)	//入队
{
	assert(pq);

	//先买一个节点
	QNode* newnode = buyNode(x);

	//分情况：如果队头为空，说明队空，此时直接将新节点赋值给队头、队尾
	if (pq->front == NULL)
	{
		pq->front = pq->rear = newnode;
		pq->size++;
	}
	else
	{
		//否则就是将新节点，链接到队尾，然后更新队尾
		pq->rear->next = newnode;	//链接
		pq->rear = newnode;	//更新队尾
		pq->size++;
	}
}

队列入队

出队

  • 即单链表的头删
  • 利用临时指针，存储当前 队头指针 的信息
  • 队头向后移动，即更新 队头指针
  • 释放临时指针
  • 队列长度 - 1
void QueuePop(Queue* pq)	//出队
{
	assert(pq);
	assert(!QueueEmpty(pq));	//如果队空，是不能出队的

	//出队思想：有元素才能出队，更新队头，销毁原队头
	QNode* cur = pq->front;
	pq->front = pq->front->next;	//更新队头指针
	free(cur);
	cur = NULL;
	pq->size--;
}

队列出队

📃查看队头、队尾元素

这两个都是甜品函数，直接一行代码解决

查看队头

  • 判断队列是否为空
  • 不为空才能查看，队头元素为 队头指针 的指向值
QListDataType QueueFront(Queue* pq)	//查看队头元素
{
	assert(pq);
	assert(!QueueEmpty(pq));

	return pq->front->data;
}

查看队尾

  • 同样需要判断队列是否为空
  • 不为空才能查看，队尾元素为 队尾指针 的指向值
QListDataType QueueRear(Queue* pq)	//查看队尾元素
{
	assert(pq);
	assert(!QueueEmpty(pq));

	return pq->rear->data;
}

📃查看队内有效元素

队列中的有效元素数，就是之前一直默默工作的 队列长度 size，直接返回它的值就好了，没什么技巧

至于为何不通过遍历的方式确定有效元素数

  • 时间成本太高，如果队列中有10w个元素，那么在调用此函数时，会很浪费时间
  • 结构设计时 size 的加入，能很好的避免这个问题，因为 size 在改变时，总是伴随着入队或出队，默默记录，效率是很高
int QueueSize(Queue* pq)	//当前队列的有效元素数
{
	assert(pq);

	return pq->size;	//直接返回就行了
}

📃判断队是否为空

此时判断队列是否为空，有多种方法

  • 通过 size 判断，为0，说明队列为空
  • 通过 队头指针 或 队尾指针 判断，为空说明队空

这里使用第二种方法，通过 队头指针 进行判断
当然，返回值是 布尔值 ，同样是利用了判断式的返回值

bool QueueEmpty(Queue* pq)	//判断当前队空情况
{
	assert(pq);

	return pq->front == NULL;
}

至此，队列 结束，结构体嵌套 也就是个纸老虎，实际还没有 二级指针 复杂，可以把 链队列 看作 单链表 的青春版

下面是程序运行图，同样是动图，可以耐心看完
队列运行动图

📖源码区

注意：为了避免文章过长，现采取 Gitee 仓库分享代码的形式，秉持开源精神，所有代码都可参考!

📃栈

这是属于栈的文件夹

📃队列

这是属于队列的文件夹

📖相关OJ试题推荐

一如既往的OJ试题推荐环节，这次是 栈和队列 专场

  • 20.有效的括号
  • 225.用队列实现栈
  • 232.用栈实现队列
  • 622.设计循环队列(中等)

📘总结

栈和队列 是两种比较特殊的数据结构，在实际中往往很少单独去使用，都是用来配合实现其他数据结构，比如 二叉树 的 层序遍历 中会用到 队列 ，很多OJ试题也会爱考这两种数据结构，因此学好它们还是很重要的

如果你觉得本文写的还不错的话，期待留下一个小小的赞👍，你的支持是我分享的最大动力！

如果本文有不足或错误的地方，随时欢迎指出，我会在第一时间改正

星辰大海

…

相关文章推荐
数据结构 | 顺序表
数据结构 | 时间复杂度与空间复杂度
数据结构 | 单链表

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/30960.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

化工机械基础试题及答案

化工机械基础试题及答案

一、 名词解释（10分） 1、无力矩理论：在旋转薄壳的受力分析中忽略了弯矩的作用，该情况下的应力状态和承受内压的薄膜相似，又称薄膜理论。 2、法兰的公称压力：以16MnR在200℃时的力学性能为基础，其…
阅读更多...
力扣刷题(代码回忆录)——动态规划

力扣刷题(代码回忆录)——动态规划

关于动态规划，你该了解这些！动态规划：斐波那契数动态规划：爬楼梯动态规划：使用最小花费爬楼梯本周小结！（动态规划系列一）动态规划：不同路径动态规划：不同路径…
阅读更多...
在vmware虚拟机中安装Linux系统CentOS7详细教程

在vmware虚拟机中安装Linux系统CentOS7详细教程

一、CentOS的下载 CentOS是免费版，推荐在官网上直接下载。 https://www.centos.org/download/ DVD ISO：普通光盘完整安装版镜像，可离线安装到计算机硬盘上，包含大量的常用软件，一般选择这种镜像类型即可。 Everythin…
阅读更多...
使用html+css+js实现一个静态页面（含源码）

使用html+css+js实现一个静态页面（含源码）

🎉精彩专栏推荐 💭文末获取联系 ✍️ 作者简介: 一个热爱把逻辑思维转变为代码的技术博主 💂 作者主页: 【主页——🚀获取更多优质源码】 🎓 web前端期末大作业： 【📚毕设项目精品实战案例 (10…
阅读更多...
A Review of Generalized Zero-Shot Learning Methods

A Review of Generalized Zero-Shot Learning Methods

摘要 生成式零样本目的是训练一个模型，监督学习下，输出类别不可知条件下，该模型对数据样本进行分类。为了解决这个任务，生成式零样本利用可见的语义信息和不可见类别在不可见和可见类别间构建桥梁，结论，许…
阅读更多...
一篇文章带你搞懂使用PID

一篇文章带你搞懂使用PID

节选自本人博客：https://www.blog.zeeland.cn/archives/pid-learning 本文为笔者参考了网上众多大神的解析之后加上自己的理解整合起来的，因此在内容上部分参考了其他作者，目的仅用作参考以便更好地学习，如有侵犯，可联…
阅读更多...
慎投：这两本期刊被剔除SCI/SSCI, 11月WOS数据库已更新~

慎投：这两本期刊被剔除SCI/SSCI, 11月WOS数据库已更新~

2022年11月22日, Clarivate更新了Journal List, 虽然影响因子每年仅更新一次，但是WOS数据库每个月都会不定期地进行调整，经过审查陆续将部分期刊剔除或新增。 本次更新，SCIE&SSCI期刊数据库剔除(Dropped)或停止检索(Ceased)了6本期刊&am…
阅读更多...
运动装备品牌排行榜，运动爱好者必备好物分享

运动装备品牌排行榜，运动爱好者必备好物分享

健身运动就像打游戏一样，如何区分你和其他玩家的差别呢？有时候靠身材，当然有时候也会拼装备，那么这些运动装备能否增加buff呢？是否值得入手呢？作为一名资深的运动爱好者，下面我就从实用角度聊一…
阅读更多...
计算机组成原理4小时速成：硬件软件，编译，控制器，存储器，运算器，输入输出设备，存储字长

计算机组成原理4小时速成：硬件软件，编译，控制器，存储器，运算器，输入输出设备，存储字长

计算机组成原理4小时速成：硬件软件，编译，控制器，存储器，运算器，输入输出设备，存储字长 2022找工作是学历、能力和运气的超强结合体，遇到寒冬，大厂不招人，可能…
阅读更多...
软件测试V模型

软件测试V模型

以“编码”为黄金分割线，将整个过程分为开发和测试，并且开发和测试之间是串行的关系 特点： 明确标注了测试的类型 明确标注了测试阶段和开发阶段之间的对应关系 缺点： 测试后置 V模型是基于瀑布模型的，将测试放在…
阅读更多...
PowerShell 批量部署windows_exporter到所有Windows主机

PowerShell 批量部署windows_exporter到所有Windows主机

前提条件 参考 批量拷贝脚本到远程主机 $local_path"D:\PowerShell\Powershell-Windows_Admin_Center-install\" #本地脚本存放目录$Destination"d:\" #本地拷贝的脚本到目标主机的目录Invoke-Command -filepath D:\powershell-install-windows_exporter-…
阅读更多...
【构建ML驱动的应用程序】第 8 章 ：部署模型时的注意事项

【构建ML驱动的应用程序】第 8 章 ：部署模型时的注意事项

🔎大家好，我是Sonhhxg_柒，希望你看完之后，能对你有所帮助，不足请指正！共同学习交流🔎 📝个人主页－Sonhhxg_柒的博客_CSDN博客 📃 🎁欢迎各位→点赞…
阅读更多...
11个步骤完美排查服务器是否被入侵

11个步骤完美排查服务器是否被入侵

随着开源产品的越来越盛行，作为一个Linux运维工程师，能够清晰地鉴别异常机器是否已经被入侵了显得至关重要，个人结合自己的工作经历，整理了几种常见的机器被黑情况供参考： 背景信息：以下情况是在CentOS 6.…
阅读更多...
计算机的磁盘与中断介绍

计算机的磁盘与中断介绍

磁盘 大多数计算机都有磁盘。这只是连接到I/O总线的另一个外围设备。磁盘的任务非常简单；它可以做两件事：存储你发给它的字节，它发送给你之前存储的字节。 大多数计算机都有磁盘有两个原因。首先，它们能够存储大量字节&#xff0c…
阅读更多...
微信小程序实现一些优惠券/卡券

微信小程序实现一些优惠券/卡券

背景 👏 前几周有小伙伴问我如何用css实现一些优惠券/卡券，今天就来分享一波吧！速速来Get吧~ 🥇文末分享源代码。记得点赞关注收藏！ 1.实现效果 2.实现原理 2.1 实现内凹圆角 假设我们要实现这样的一个效果&#xf…
阅读更多...
Java八股文

Java八股文

2022年接近年底了，想必绝大多数的小伙伴跳槽的心已经蠢蠢欲动。但一边又是互联网寒冬、大厂裁员，导致人心惶惶，想跳又不敢跳。但现在罡哥，给大家整理了八股文大厂面试真题和面试技巧。这里免费分享给大家。 资料包括：…
阅读更多...
算法day29|491，46，47

算法day29|491，46，47

491.递增子序列 class Solution:def findSubsequences(self, nums: List[int]) -> List[List[int]]:used [False]*len(nums)result []nums.sort()def backtracking(nums,path,startindex,used):nonlocal resultif len(path)>1:result.append(path[:])for i in range(s…
阅读更多...
云原生系列 五【轻松入门容器基础操作】

云原生系列 五【轻松入门容器基础操作】

✅作者简介： CSDN内容合伙人，全栈领域新星创作者，阿里云专家博主，华为云云享专家博主，掘金后端评审团成员 💕前言： 最近云原生领域热火朝天，那么云原生是什么？何为云原生…
阅读更多...
C＜6.1＞函数习题（函数内测整形数组大小，递归

C＜6.1＞函数习题（函数内测整形数组大小，递归

目录 1，数组比较 2，勒让德多项式 3，查询数组（sizeof问题 1，数组比较 1. 编写函数实现比较两个长度为 n（n 可变）的数组大小。比较逻 辑如下： 假设 a 和 b 为 n 个元素的整型数组&am…
阅读更多...
Web(一)Web前端开发概述

Web(一)Web前端开发概述

第1关_Web前端开发相关的概念 相关知识 为了完成本关任务，你需要掌握：1.Web系统的组成；2.浏览器的概念；3.URL的概念；4.Web标准。 Web系统的组成：Web是Internet上最受欢迎的一种多媒体信息服务系统。 整个…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023