文章目录
- 树与森林
- 树结构初识
- 树基本的相关概念
- 森林
- 二叉树(Binary Tree)
- 满二叉树【饱满】
- 完全二叉树【少了叶子的满二叉树】
- 总结
- 树和森林的转换
- 快速转换技巧
- 森林转化为二叉树
- 分辨
- 二叉树的五大性质
树与森林
- 树是一种的数据结构。顾名思义,类似于我们生活中的树一样。【具体一点就是一对多的数据结构】
树结构初识
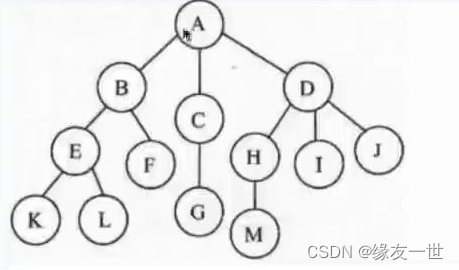
- 从最上面的根节点的节点开始像下面进行延申,更多的节点,这种结构就称为树(Tree)。
- 注意分支只能向后单向延申,不能与其他分支上的结点相交。
树基本的相关概念
| 术语 | 解释 |
|---|---|
| 根节点 | 位于最上面的结点。 |
| 度 | 每个节点连接的子节点数目(分支的数目)。 |
| 树的度 | 一棵树中各个结点度的最大值。 |
| 子树 | 每个节点延伸下去的下一个节点都可以称为一棵子树。 |
| 结点的层次(Level) | 按照从上往下的顺序,树的根节点的层次为1,每向下一层+1 |
| 树的层次(Depth) | 整棵树中所有结点的最大层次。 |
| 子节点(Child) | 与当前结点直接向下相连的结点 |
| 父节点(Parent) | 与当前结点直接向上连接的结点 |
| 兄弟结点(Sibling) | 两个结点的父节点相同 |
| 祖宗结点(Ancestor) | 从根节点开始一直到某个结点的整条路径的所有结点,都是当前结点的祖宗节点 |
| 叶子结点 | 度为0的结点【一般位于分支的最末端】 |
| 分支结点 | 度为1或2的非根节点 |
森林
- 一片森林是由很多课树构成。
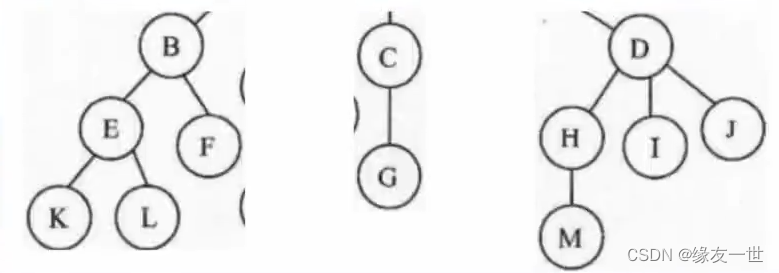
- 各个树之间互不连接。
二叉树(Binary Tree)
- 二叉树是一种特殊的树,它的度最大只能为2。
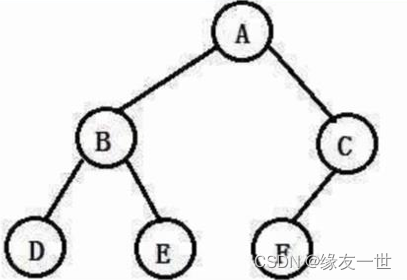
- ***二叉树的结点的子树是有左右之分的,不能颠倒顺序。***A左边的子树为左子树,A右边的树为右子树。
- 二叉树的五种基本形态

满二叉树【饱满】
- 满二叉树:所有的分支结点都存在左子树和右子树,且叶子结点都在同一层。
- 整棵树都是很饱满的,没有度为1的结点。
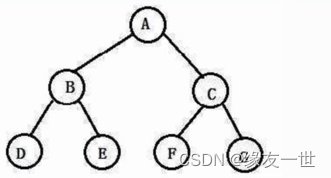
完全二叉树【少了叶子的满二叉树】
- 只有最后一层有空缺,并且所有的叶子节点是按照从左到右的顺序排列的。
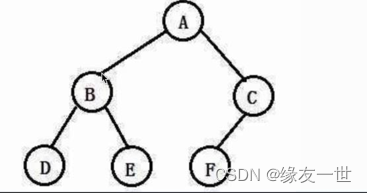
总结
- 一颗满二叉树一定是一个课完全二叉树。完全二叉树一定不是满二叉树【但完全二叉树是一颗少了叶子的满二叉树】。
树和森林的转换
- 普通树转换为二叉树的转换规则
- 孩子结点->左子树结点(左孩子)
- 兄弟节点->右子树结点(右兄弟)
- 规律:一颗普通树转化为二叉树后2,跟结点一定没有左子树。
- 普通树
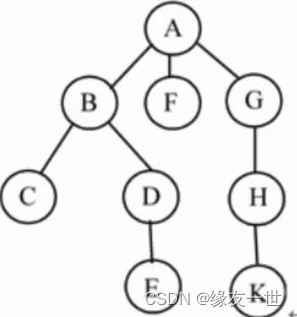
- 转换后的二叉树
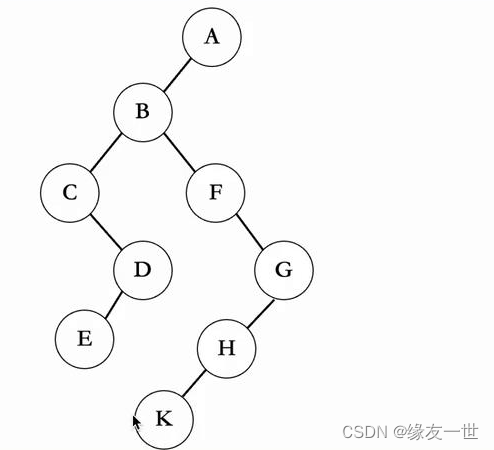
快速转换技巧
- 第一步:直接将从最左端开始将所有的兄弟节点连接起来。
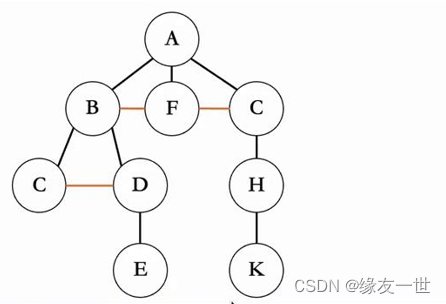
- 第二步:然后擦除所有结点除了最左边结点以外的连线。
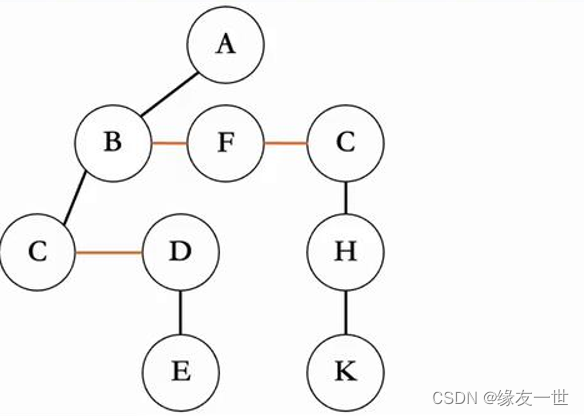
- 第三步:所有的黑色连线偏向左,橙色连线偏向右

森林转化为二叉树
- 第一步:先将森林中的所有普通树转化为二叉树。
- 第二步:然后依次相连【右兄弟】
- 森林
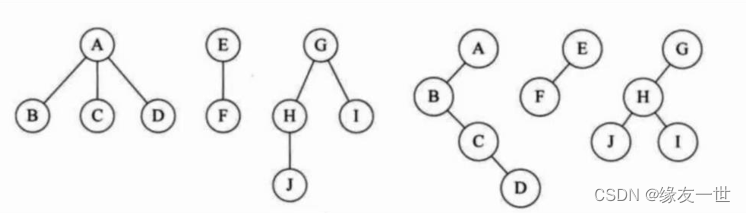
- 转化后的二叉树
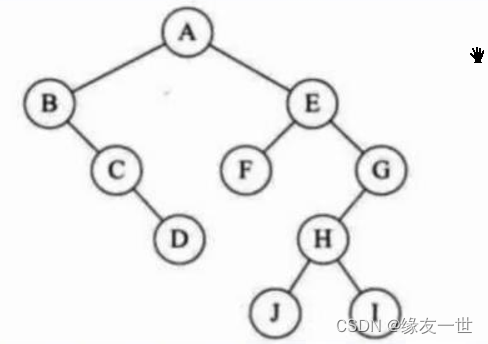
- 连接每棵树时,都是从根节点的右边开始,不断向右连接。
分辨
- 如果二叉树的根节点有右兄弟结点,则它是由森林转换而来。否则,它是由一棵树转换而来。
二叉树的五大性质
-
性质一:对于一颗二叉树,第i层的最大结点数量为
2 i − 1 2^{i-1} 2i−1 -
性质二:对于一颗深度为k的二叉树,可以具有的最大结点数量为:
n = 2 0 + 2 1 + 2 2 + . . . + 2 k − 1 n=2^0+2^1+2^2+...+2^{k-1} n=20+21+22+...+2k−1
简化计算
S n = a 1 × ( 1 − q n ) 1 − q = 1 × ( 1 − 2 k ) 1 − 2 = − ( 1 − 2 k ) = 2 k − 1 S_n=\frac{a_1\times(1-q^n)}{1-q}=\frac{1\times(1-2^k)}{1-2}=-(1-2^k)=2^k-1 Sn=1−qa1×(1−qn)=1−21×(1−2k)=−(1−2k)=2k−1- 结论:
- 一颗深度为k的二叉树最大结点数量为 2 k − 1 2^k-1 2k−1,结点的边数为 E = n − 1 E=n-1 E=n−1
- 结论:
-
性质三:【记忆】
n 0 = n 2 + 1 n_0=n_2+1 n0=n2+1- 假设一颗二叉树中度为0、1、2的结点数量为
n
0
、
n
1
、
n
2
n_0、n_1、n_2
n0、n1、n2,由于一棵树二叉树中只有这三种类型的结点,可得结点总数:
n = n 0 + n 1 + n 2 n=n_0+n_1+n_2 n=n0+n1+n2 - 从二叉树的边数考虑,因为每个结点有且仪有一条边与具交结点相连,那么边数之和就可以表示为
E = n 1 + 2 n 2 E=n_1+2n_2 E=n1+2n2 - 度为1的结点有一条边,度为2的结点有两条边,度为0的结点没有,加在一起就是整棵二叉树的边数之和,可得
E = n − 1 = n 1 + 2 n 2 n = n 1 + 2 n 2 + 1 E=n-1=n_1+2n_2 n=n_1+2n_2+1 E=n−1=n1+2n2n=n1+2n2+1 - 再结合第一个公式
n 0 = n 2 + 1 n_0=n_2+1 n0=n2+1
- 假设一颗二叉树中度为0、1、2的结点数量为
n
0
、
n
1
、
n
2
n_0、n_1、n_2
n0、n1、n2,由于一棵树二叉树中只有这三种类型的结点,可得结点总数:
-
性质四:【记忆】
- 完全二叉树除了最后一层有空缺外,其他层数都是饱满的,假设这模二叉树为满二叉树,那么根据我们前面得到的性质,假设层数为
k
k
k,那么结点数量为:
n
=
2
k
−
1
n=2^k-1
n=2k−1,根据完全二叉树的性质,最后一层可以满可以不满,那么一棵完全二叉树结点数
n
n
n满足:
2 k − 1 − 1 < n < = 2 k − 1 2^{k-1}-1<n<=2^k-1 2k−1−1<n<=2k−1 - 因为n肯定是一个整数,那么可以写为
2 k − 1 < = n < = 2 k − 1 2^{k-1}<=n<=2^k-1 2k−1<=n<=2k−1 - 现在我们只看左边的不等式,我们对不等式两边同时取对数,得到
k − 1 < = l o g 2 n k-1<=log_2n k−1<=log2n - 综上所述,一棵具有n个结点的完全二叉树深度为
k = l o g 2 n + 1 k=log_2n+1 k=log2n+1
- 完全二叉树除了最后一层有空缺外,其他层数都是饱满的,假设这模二叉树为满二叉树,那么根据我们前面得到的性质,假设层数为
k
k
k,那么结点数量为:
n
=
2
k
−
1
n=2^k-1
n=2k−1,根据完全二叉树的性质,最后一层可以满可以不满,那么一棵完全二叉树结点数
n
n
n满足:
-
性质五:
- 一颗有n个结点的完全二叉树,由性质四得到深度为k=log2+1现在对于任意一个结点i,结点的顺序为从上往
下,从左往右: - 对于一个拥有左右孩子的结点来说,其左孩子为 2 i 2i 2i,右孩子为 2 i + 1 2i+1 2i+1。
- 如果 i = 1 i=1 i=1,那么此节点为二叉树的根节点,如果 i > 1 i>1 i>1,那么其父节点为 ⌊ i / 2 ⌋ \lfloor i/2 \rfloor ⌊i/2⌋
- 如果 2 i > n 2i>n 2i>n,则结点 i i i没有左孩子
- 如果 2 i + 1 > n 2i+1>n 2i+1>n,则结点i没有右孩子
- 一颗有n个结点的完全二叉树,由性质四得到深度为k=log2+1现在对于任意一个结点i,结点的顺序为从上往