一、堆

1、什么是堆？

在前面的章节中，我们了解到了树、二叉树等相关的概念，那么今天所讲解的堆就是基于二叉树中的完全二叉树实现的。那么在完全二叉树的基础上，堆还满足该性质：堆中的子节点始终小于等于（大于等于）父节点。

倘若，堆的父节点始终小于等于其子节点，我们就称之为小根堆。
倘若，堆的父节点始终大于等于其子节点，我们就称之为大根堆。

堆的逻辑结构及物理结构;

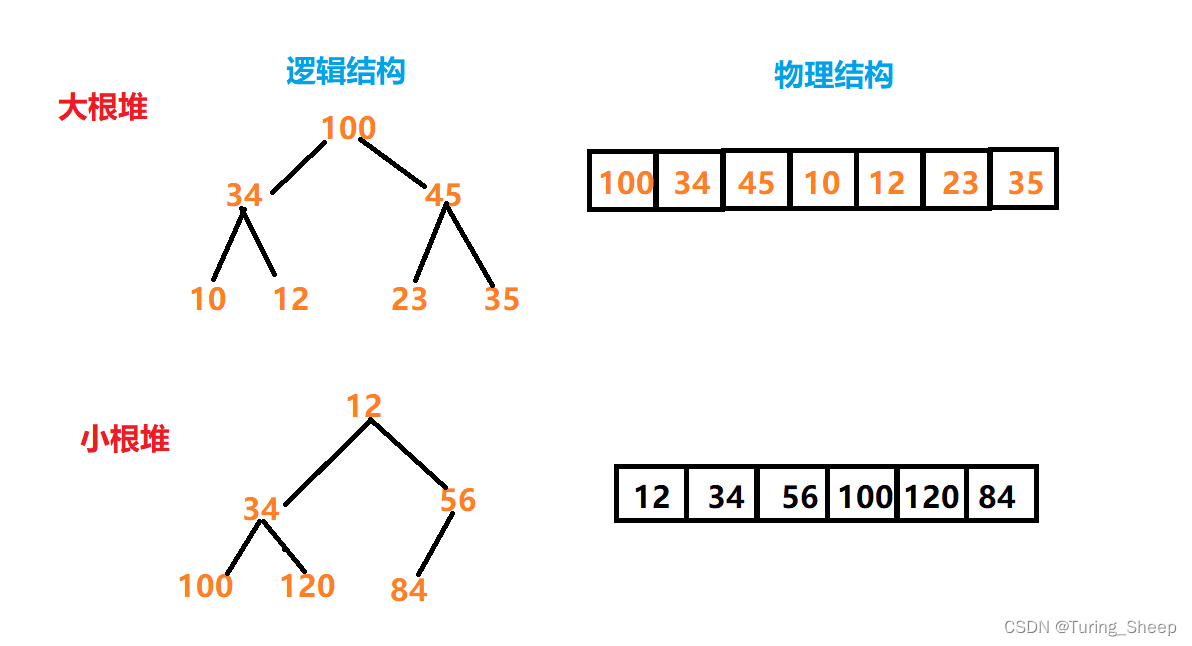
从上述的物理结构我们可以知道，我们接下来的代码实现是基于数组的。因此，我们将采用动态顺序表的思路来存储堆。

2、堆的实现

（1）堆的定义

typedef int ElementType;
typedef struct Heap
{
	ElementType* a;
	int size;
	int capacity;
}Heap;

（2）接口函数

初始化

void HeapInit(Heap* h)
{
	assert(h);
	h->a=NULL;
	h->size=h->capacity=0;
}

销毁

void HeapDestory(Heap* h)
{
	assert(h);
	free(h->a);
	h->a = NULL;
	h->size = h->capacity = 0;
}

插入

因为我们是在数组中实现堆的，但是数组在中部插入的时间复杂度是O(N)，头部插入的时间复杂度也是O(N)。因此，我们是在最后一个位置插入一个数据，然后再让这个数据向上移动。但是我们新插入的节点如何向前移动？

在下面的小根堆中，我们假设在尾部插入一个1。

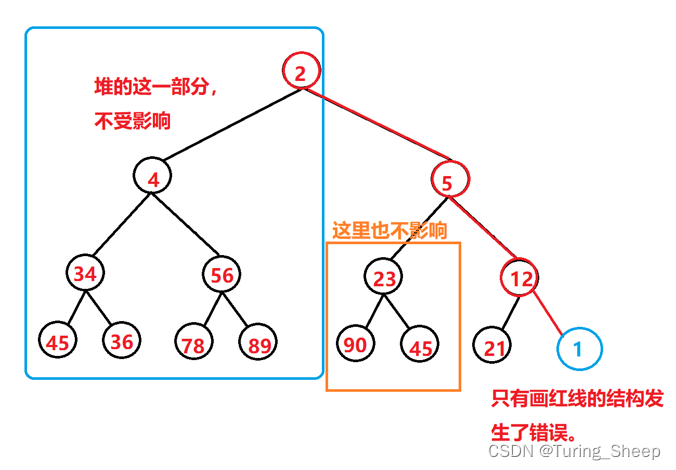
从图中我们能够看出，我们将一个数据向上进行调整的时候，我们只需要关注该节点所在的路径。我们不妨把这条线抽离出来：

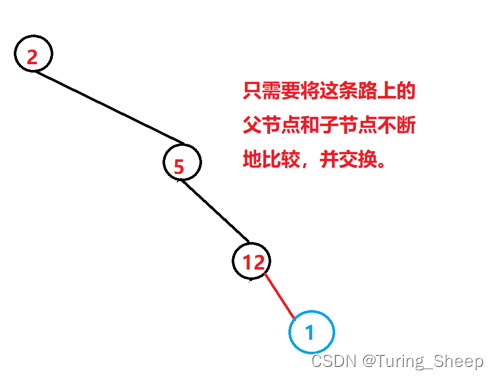
此时，我们发现，1需要向上移动的话，只需要和1的祖宗们相比较。因此，我们可以写出AdjustUp的函数。

void AdjustUp(Heap* h, int child)
{
	assert(h);
	while (child>0)
	{
		int parent = (child - 1) >> 1;
		if (h->a[child] < h->a[parent])
		{
			ElementType tmp = h->a[child];
			h->a[child] = h->a[parent];
			h->a[parent] = tmp;
			child = parent;
		}
		else
		{
			break;
		}
	}
}

void HeapPush(Heap* h,ElementType x)
{
	assert(h);
	if (h->size == h->capacity)
	{
		size_t newcapacity = (h->capacity == 0) ? 4 : 2 * h->capacity;
		ElementType* tmp = realloc(h->a,sizeof(ElementType)*newcapacity);
		if (tmp == NULL)
		{
			printf("realloc fail\n");
			exit(-1);
		}
		h->a = tmp;
		h->capacity = newcapacity;
	}
	h->a[h->size] = x;
	h->size++;
	AdjustUp(h,h->size-1);
}

当我们调整好后，就会出现下面的样子：

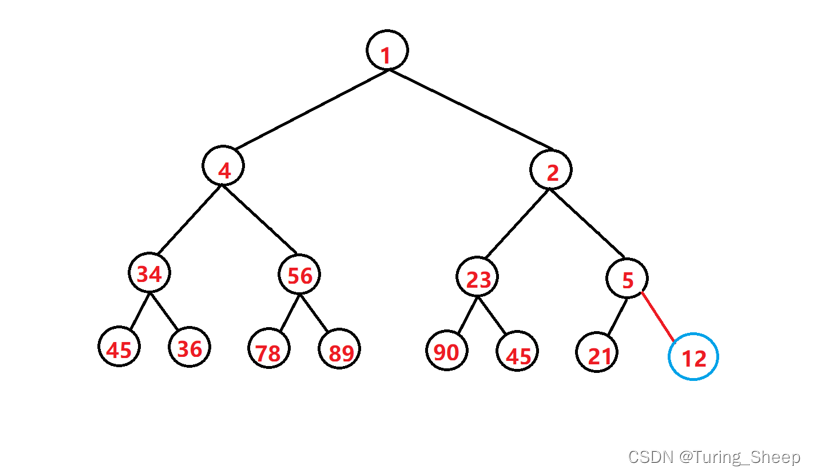
删除

在插入函数的铺垫下，这里讲解删除就好理解多了。我们的堆删除的元素一般是堆顶元素。因此，我们这里需要删除的是堆顶。但数组中删除堆顶元素的时间复杂度是O(N)。这是相当复杂的，而尾删的时间复杂度是O(1)，于是我们这里也是先将尾部元素和堆顶元素进行交换，然后再将堆顶元素向下移动。

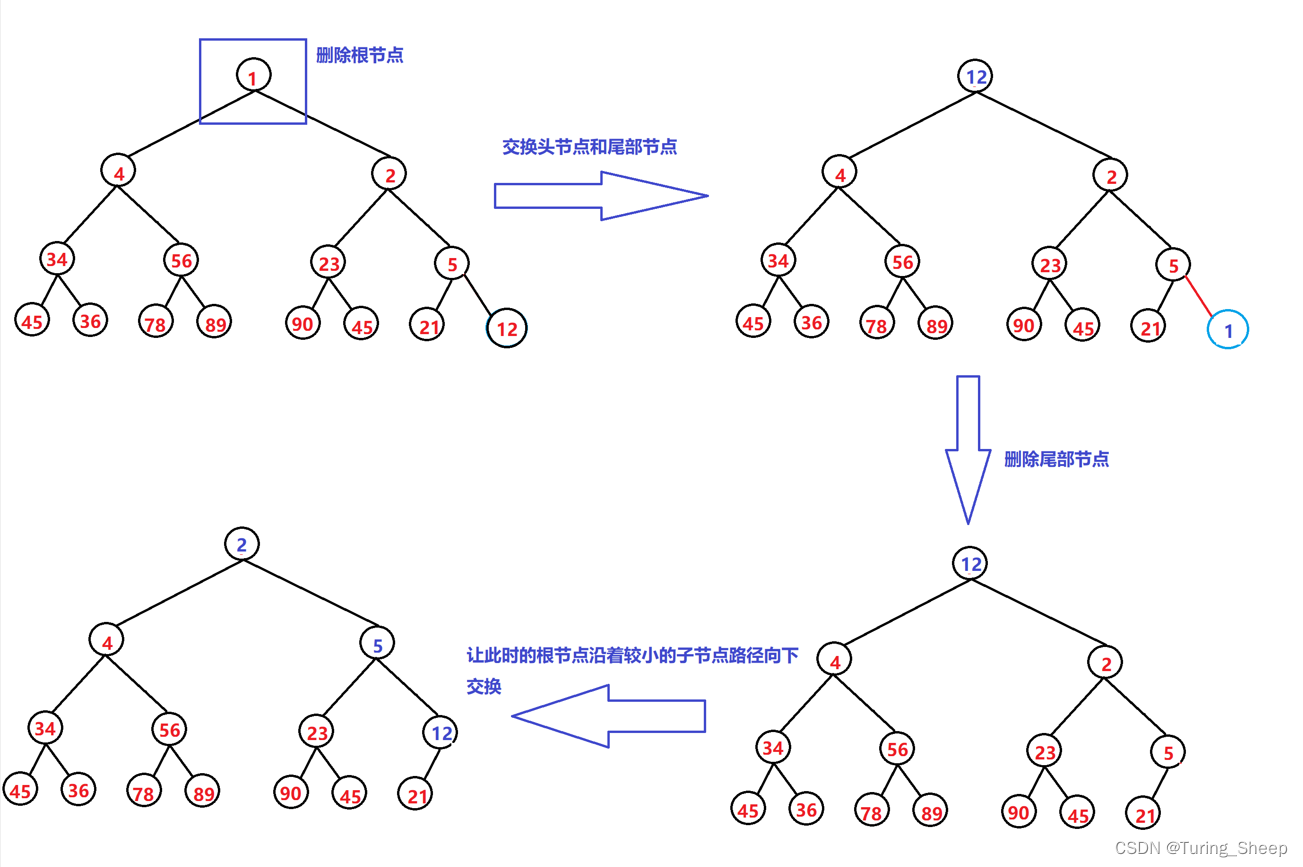
但是我们这里要解释一下：为什么要和子结点中较小的交换。

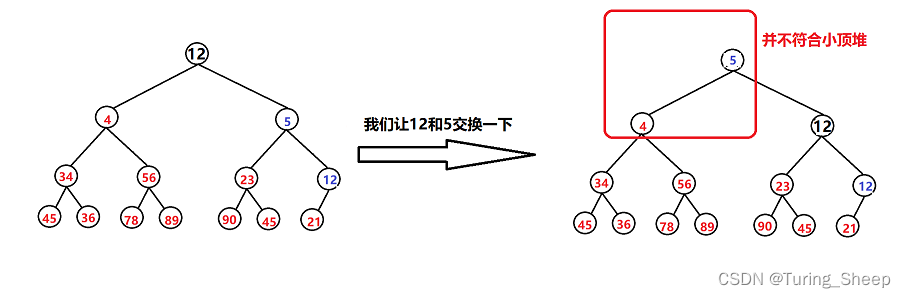
通过上述反例，我们就发现了根节点和较小子节点交换的重要性。

void AdjustDown(Heap* h, int parent)
{
	assert(h);
	int child = parent * 2 + 1;
	while (child<h->size)
	{
		if (child + 1 < h->size && h->a[child + 1] < h->a[child])
		{
			child++;
		}
		if (h->a[child] < h->a[parent])
		{
			ElementType tmp = h->a[child];
			h->a[child] = h->a[parent];
			h->a[parent] = tmp;
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapPop(Heap* h)
{
	assert(h);
	assert(!HeapEmpty(h));
	ElementType tmp = h->a[0];
	h->a[0] = h->a[h->size - 1];
	h->a[h->size - 1] = tmp;
	h->size--;
	AdjustDown(h,0);
}

判断是否为空

bool HeapEmpty(Heap* h)
{
	assert(h);
	return h->size == 0;
}

因为我们在C语言中本身是没有bool的，所以我们需要包含头文件<stdbool.h>

返回堆顶

这里要注意一下，返回之前我们要判断堆是否为空。

ElementType HeapTop(Heap* h)
{
	assert(h);
	assert(!HeapEmpty(h));
	return h->a[0];
}

返回堆中的元素个数

int HeapSize(Heap* h)
{
	assert(h);
	return h->size;
}

打印

void HeapPrint(Heap* h)
{
	assert(h);
	for (int i = 0; i < h->size; i++)
	{
		printf("%d ",h->a[i]);
	}
	printf("\n");
}

这里我们需要注意是，打印出来的是一个数组，因此，我们要根据完全二叉树的下标之间的规律去还原堆的逻辑结构。