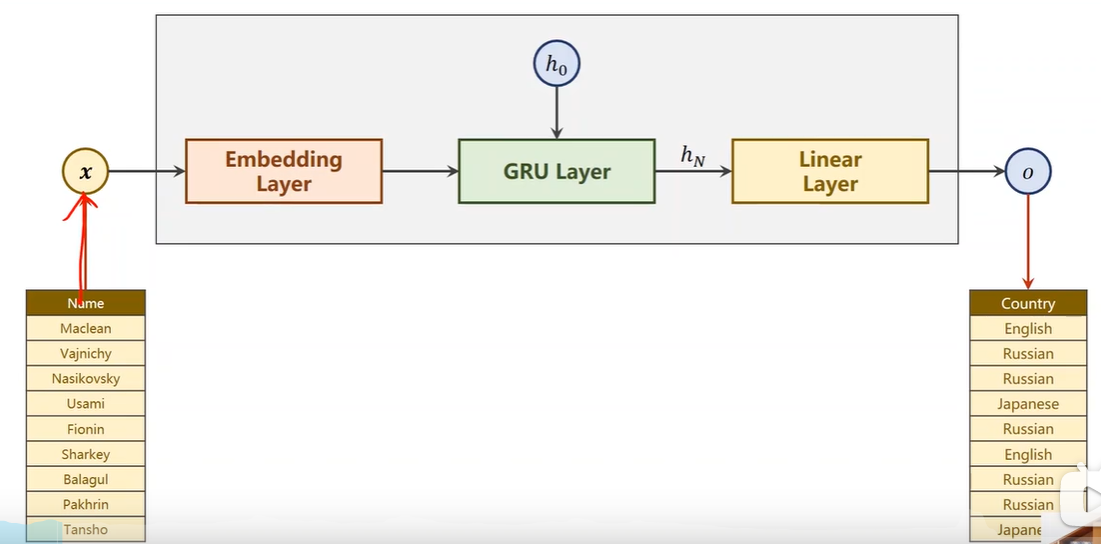
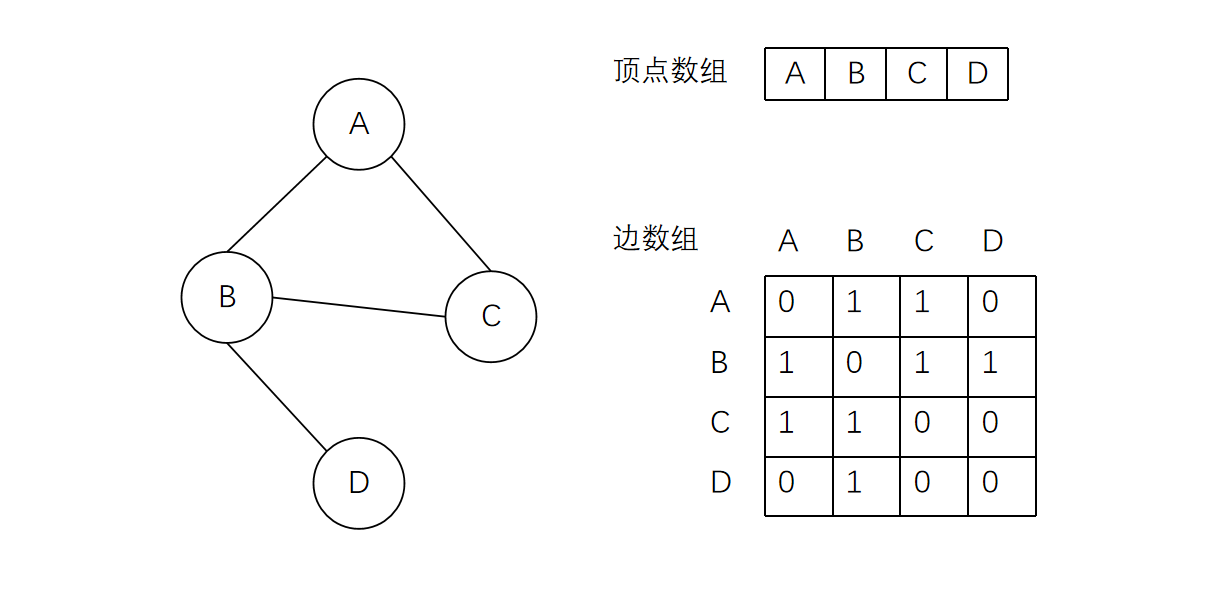
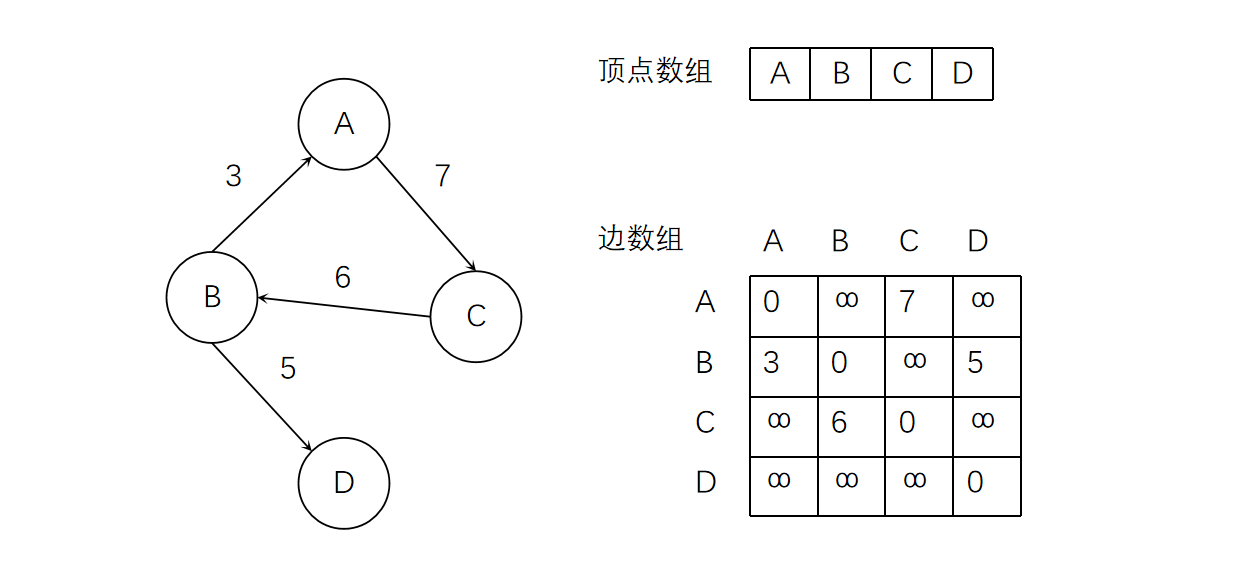
一、邻接矩阵
图的邻接矩阵存储方式就是用两个数组来表示图。一个一维数组存储图的顶点信息,另一个二维数组存储图中边的信息。
对于无向图来说,我们可以用1表示两顶点相连,用0表示两顶点不相连。任意顶点的度为邻接矩阵中该节点的行或列的元素之和。
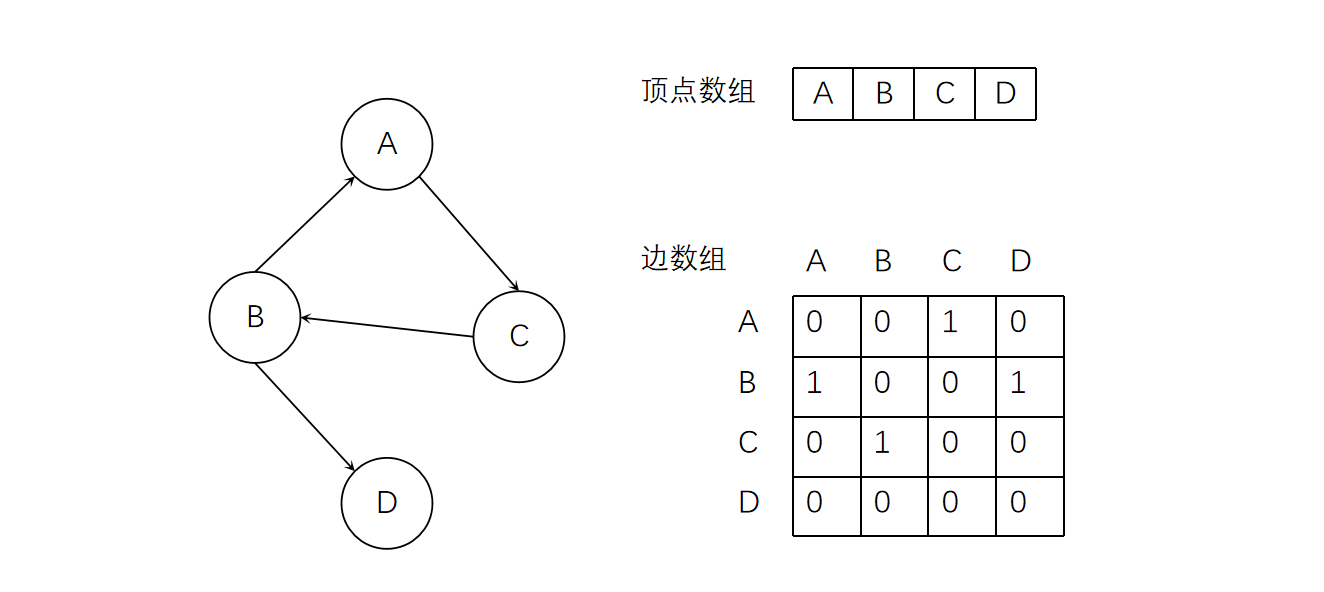
对于有向图,任意顶点的入度为其对应列的元素之和,出度为其对应行的元素之和。
对于有权图,可以将邻接矩阵中的元素存储为权值。对于不可达的顶点,可以用一个权值不可能达到的极限值表示。
代码如下
public class GraphByAdjacencyMatrix<T>:IGraph<T>
{
private T[] _nodes;
private int[,] _matrix;
private int _count;
public GraphByAdjacencyMatrix(int capacity)
{
_nodes = new T[capacity];
_matrix = new int[capacity, capacity];
// 初始化邻接矩阵
for (int i = 0; i < capacity; i++)
{
for (int j = 0; j < capacity; j++)
{
if (i == j)
_matrix[i, j] = 0;
else
_matrix[i, j] = Int32.MaxValue;
}
}
}
/// <summary>
/// 添加节点
/// </summary>
/// <param name="e"></param>
public void AddNode(T e)
{
_nodes[_count++] = e;
}
/// <summary>
/// 添加边
/// </summary>
/// <param name="node1Index"></param>
/// <param name="node2Index"></param>
/// <param name="weight"></param>
public void AddEdge(int node1Index, int node2Index, int weight)
{
_matrix[node1Index, node2Index] = weight;
}
}
因为邻接矩阵使用二维数组存储图中边的信息,所以如果图的顶点数量较多而边的数量较少时,会浪费大量的空间。
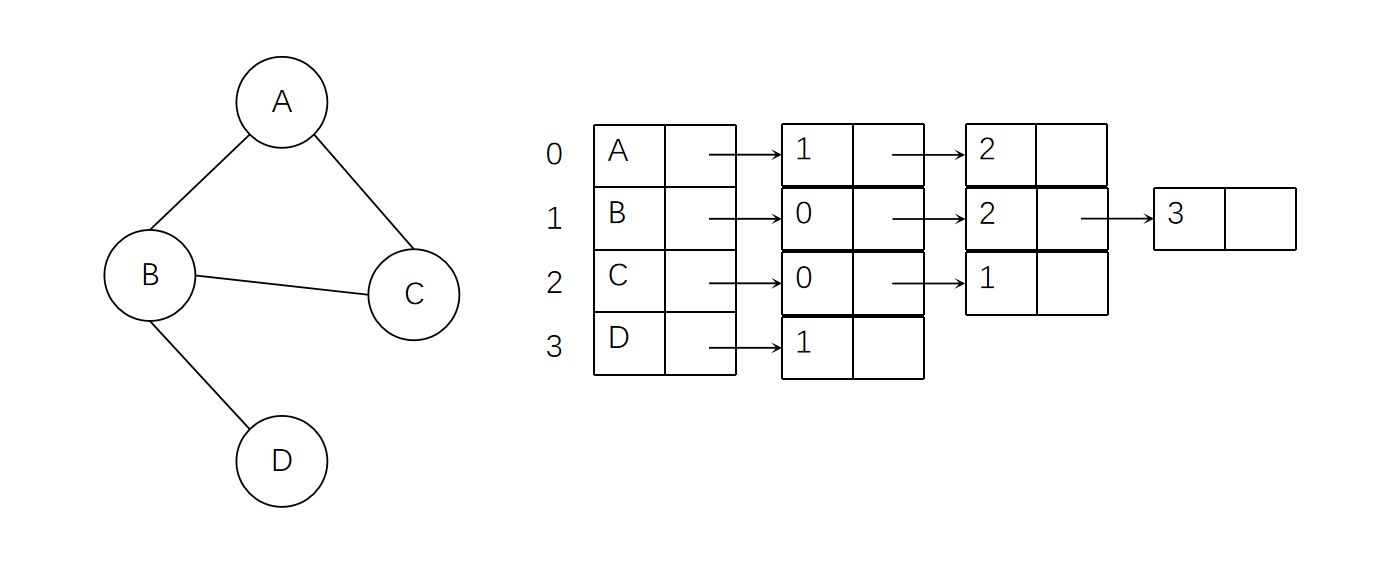
二、邻接表
为了节省空间,我们可以将邻接矩阵改为链表,即邻接表结构。图的邻接表存储方式采用一个一维数组存储顶点。这些顶点还需要存储第一个邻接点的指针,每个顶点的所有邻接点构成一个链表。
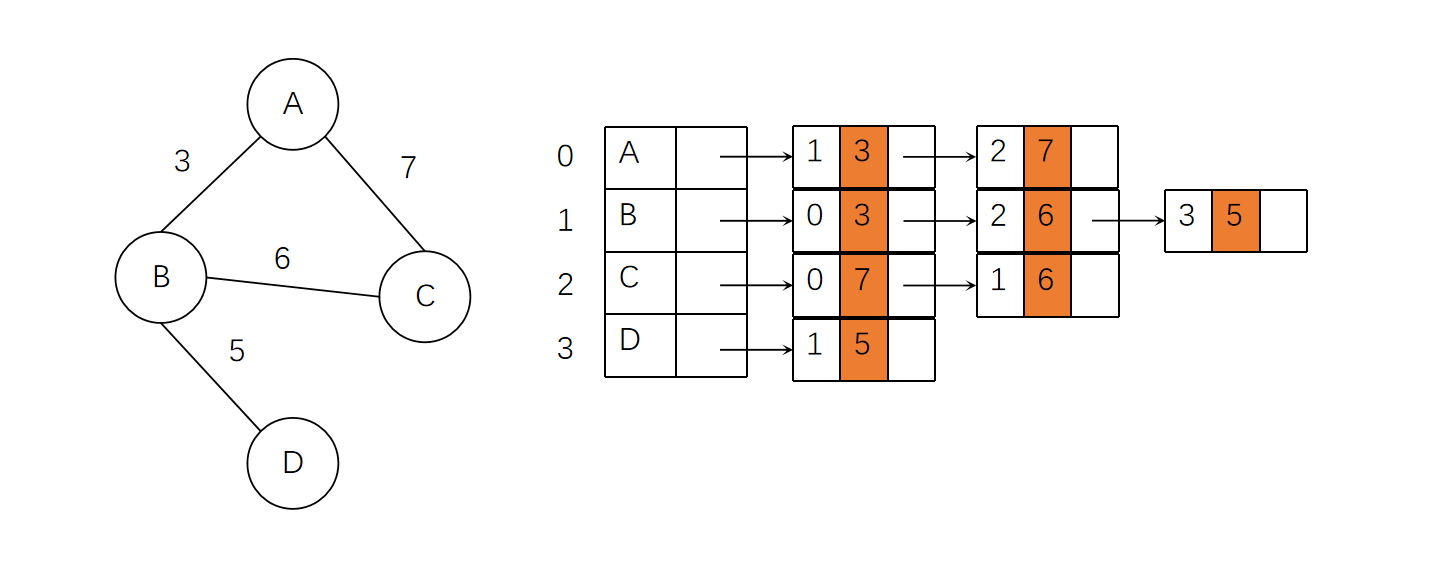
对于带权图,可以给邻接点增加一个“权值”的数据域
代码如下
public class GraphByAdjacencyList<T>:IGraph<T>
{
/// <summary>
/// 边结构
/// </summary>
class Edge
{
public int index;
public int weight;
public Edge next;
public Edge(int index,int weight)
{
this.index = index;
this.weight = weight;
}
}
/// <summary>
/// 顶点结构
/// </summary>
/// <typeparam name="T"></typeparam>
class Node<T>
{
public T data;
public Edge next;
public Node(T e)
{
data = e;
}
}
private Node<T>[] _nodes;
private int _count;
public GraphByAdjacencyList(int capacity)
{
_nodes = new Node<T>[capacity];
}
/// <summary>
/// 添加顶点
/// </summary>
/// <param name="e"></param>
public void AddNode(T e)
{
_nodes[_count++] = new Node<T>(e);
}
/// <summary>
/// 添加边
/// </summary>
/// <param name="node1Index"></param>
/// <param name="node2Index"></param>
/// <param name="weight"></param>
public void AddEdge(int node1Index, int node2Index, int weight)
{
Edge edge = new Edge(node2Index, weight);
// 头插法
edge.next = _nodes[node1Index].next;
_nodes[node1Index].next = edge;
}
}
邻接表可以有效地解决邻接矩阵浪费空间的问题,但也引入了新的问题:对于有向图来说,想要了解某个顶点的出度可以遍历顶点后的邻接点链表获得,但想要了解其入度则需要遍历整个图才能获得。
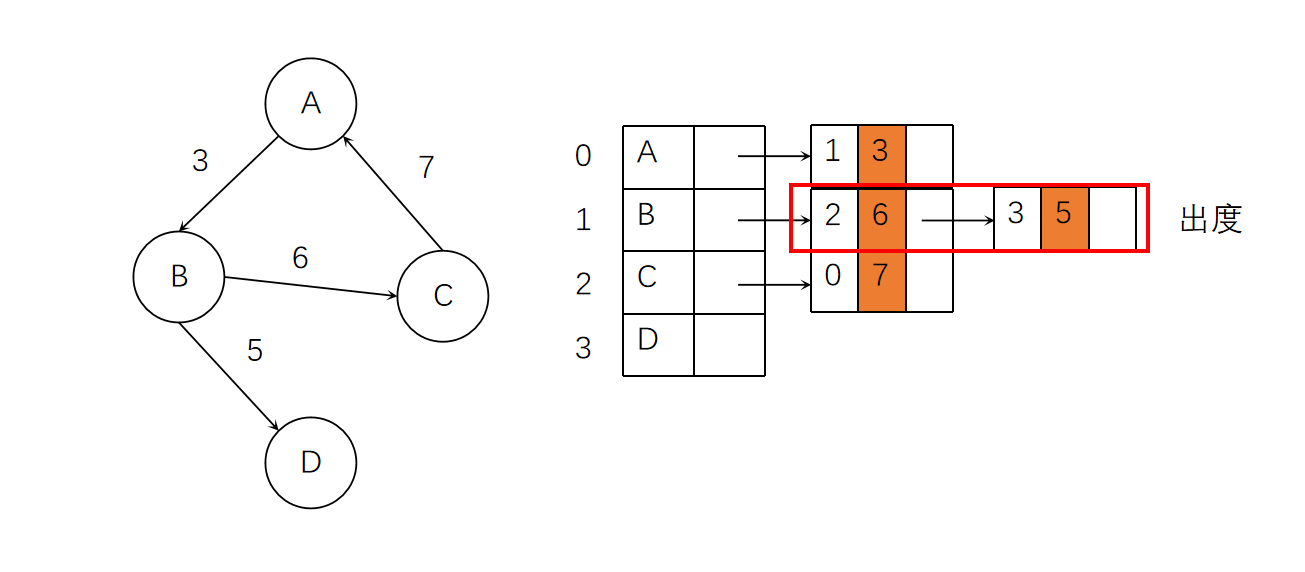
我们当然也可以将邻接表反转,将到达顶点的边作为邻接表,也就是逆邻接表。逆邻接表可以通过遍历链表来得到某个顶点的入度,但是出度则需要遍历整个图
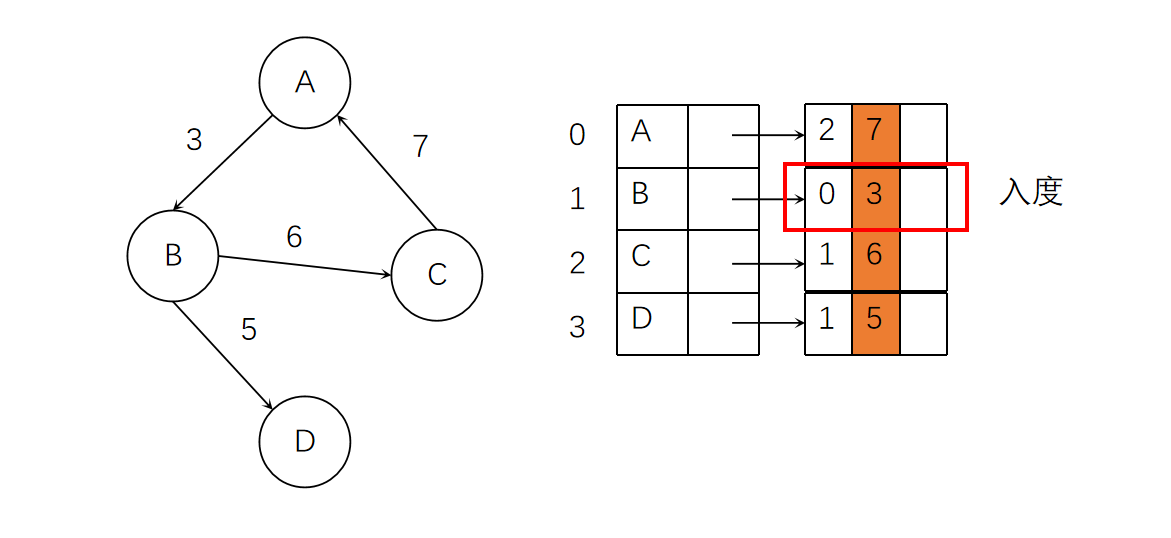
三、十字链表
对于有向图来说,无论是邻接表还是逆邻接表都无法完美地解决入度与出度的问题。但我们可以将它们整合在一起,也就是十字链表。
十字链表给顶点和边的结构都增加了几块区域用来存储额外的指针和下标。顶点结构用两个指针区域分别存储「入顶点的边的链表」与「出顶点的边的链表」指针。

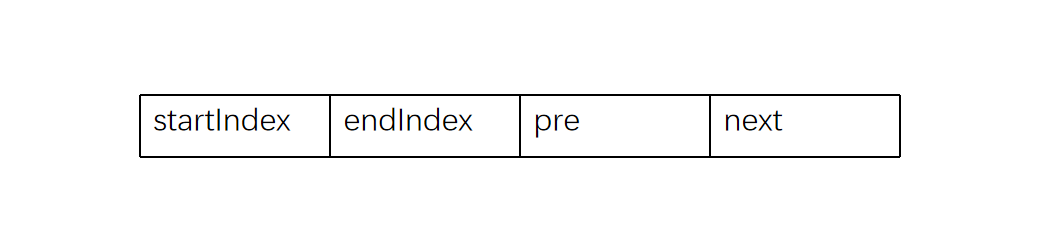
边结构用两个区域分别存储「边起始顶点的下标」与「边终止顶点的下标」,另外两个指针区域分别存储「入该顶点的下一条边」与「出该顶点的下一条边」的指针。
最终形成的结构如下
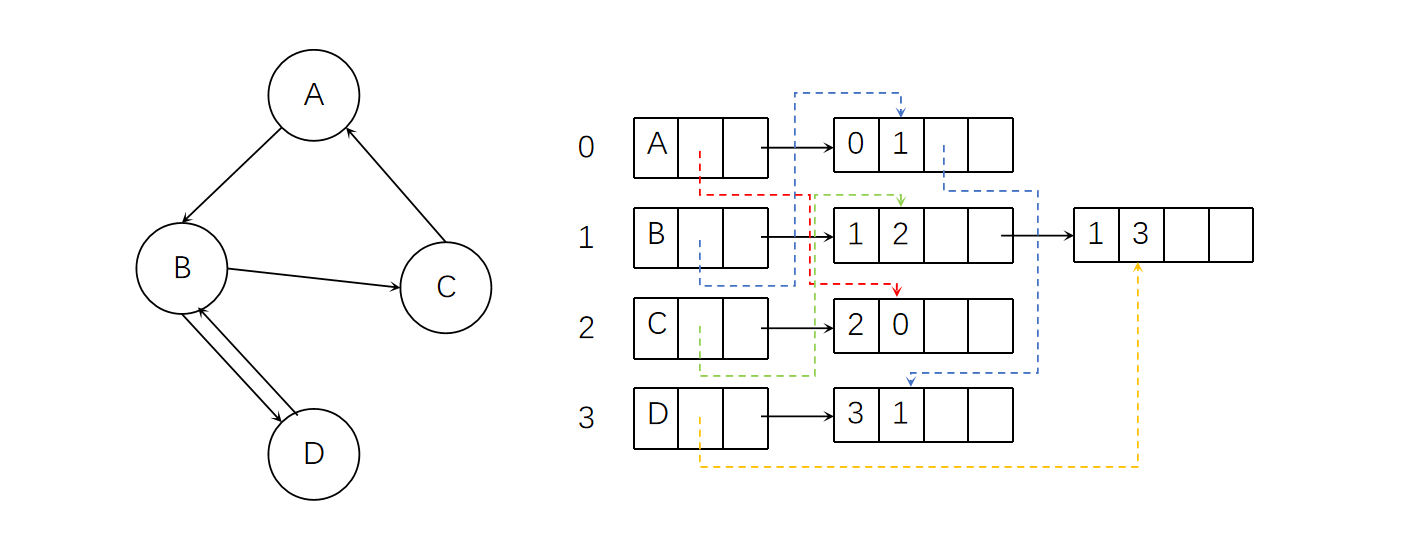
如果我们想要获取B点的出度,只需要沿着黑色箭头方向遍历;如果要获取B点的入度,只需要沿着蓝色箭头方向遍历。虽然数据结构变得更加复杂,但降低了遍历出边和入边的时间复杂度。
代码如下
public class GraphByOrthogonalList<T> : IGraph<T>
{
private class Node<T>
{
public T data;
public Edge inPointer;
public Edge outPointer;
public Node(T e)
{
data = e;
}
}
private class Edge
{
public int startIndex;
public int endIndex;
public int weight;
public Edge pre;
public Edge next;
public Edge(int startIndex,int endIndex,int weight)
{
this.startIndex = startIndex;
this.endIndex = endIndex;
this.weight = weight;
}
}
private readonly Node<T>[] _nodes;
private int _count;
public GraphByOrthogonalList(int capacity)
{
_nodes = new Node<T>[capacity];
}
public void AddNode(T e)
{
_nodes[_count++] = new Node<T>(e);
}
public void AddEdge(int node1Index, int node2Index, int weight)
{
var edge = new Edge(node1Index,node2Index,weight);
// 先插入出边
edge.next = _nodes[node1Index].outPointer;
_nodes[node1Index].outPointer = edge;
// 再插入入边
edge.pre = _nodes[node2Index].inPointer;
_nodes[node2Index].inPointer = edge;
}
}
四、邻接多重表
邻接表对于无向图来说同样存在某些问题。比如如果我们需要删除下图中B->C的边,就需要删除邻接表中的两个节点。要找到这两个节点,就需要对B的邻接链表和C的邻接链表分别进行遍历。
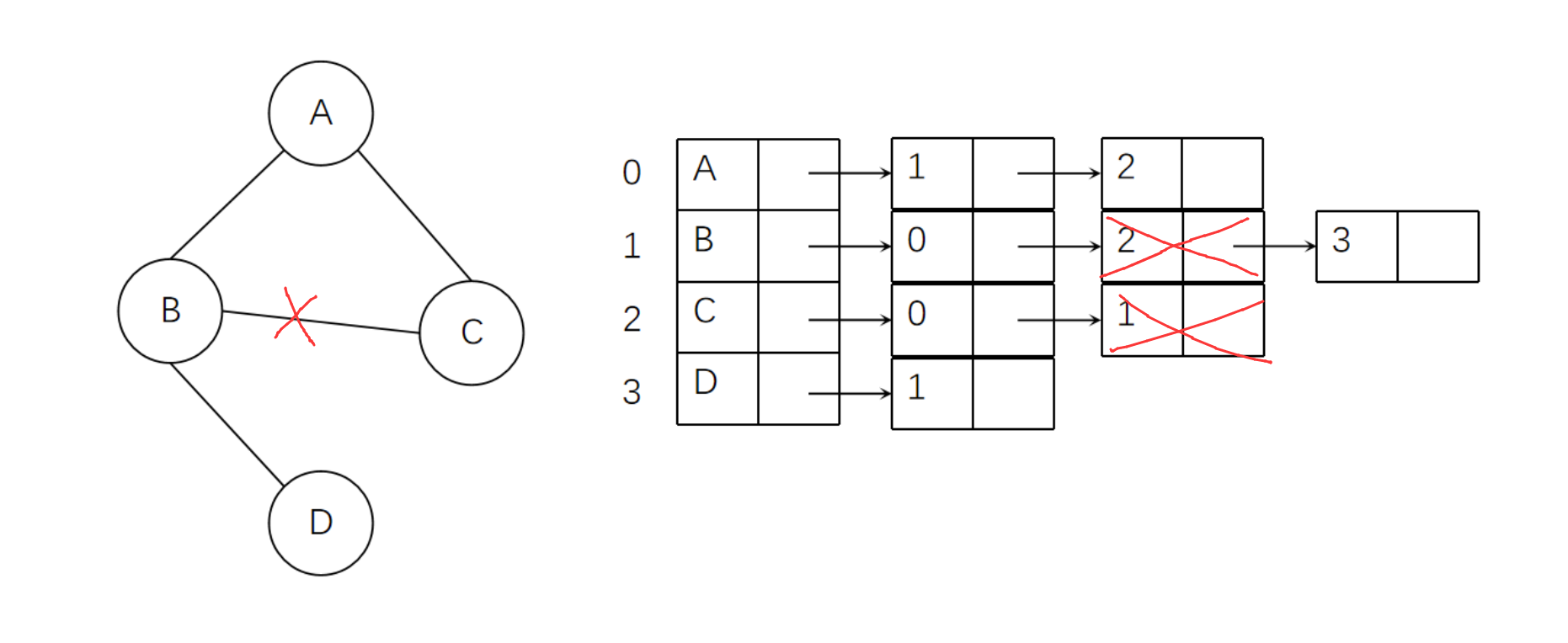
为了解决这一问题,我们需要对边结构进行如下改造。index1和index2分别存储这条边连接的两个顶点。next1指向依附index1的下一条边,next2指向依附index2的下一条边。
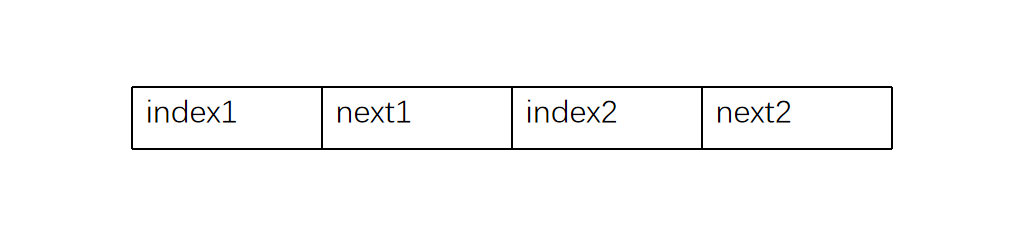
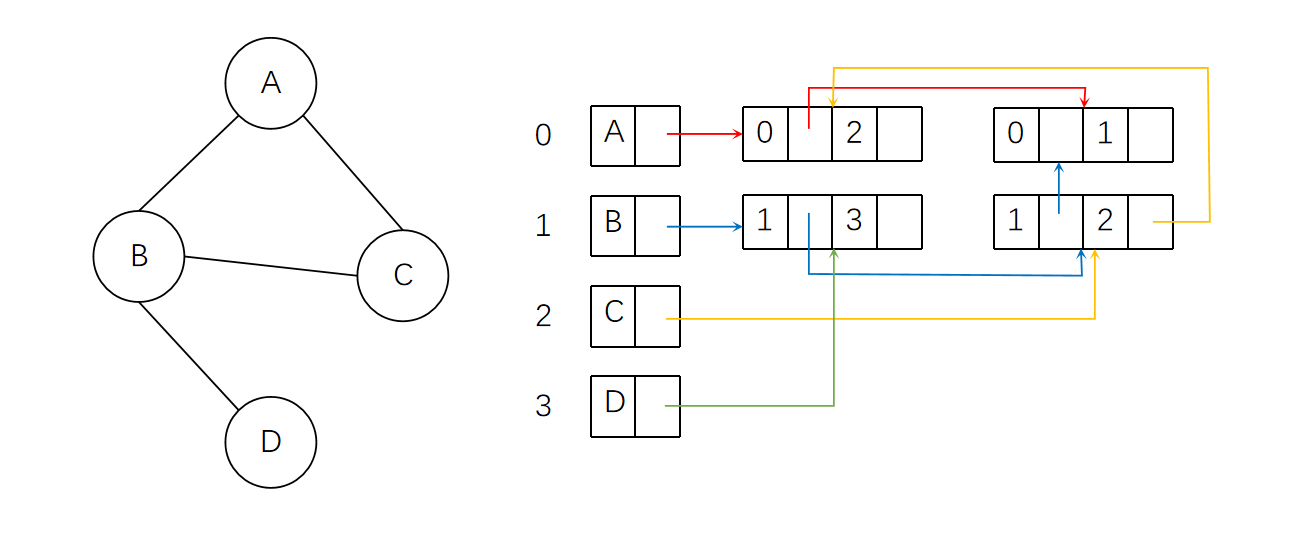
图的邻接多重表结构如下。可能有些凌乱,但其核心思想就是将原本需要两个节点表示的边简化为一个节点表示。为了让一个节点能够表示一条边,理所当然的就要存储起止节点的下标。同时,因为每条边都必定与两个顶点相连,所以就需要两个指针域分别存储对应顶点的指针。
比如对于B顶点来说,有三条从自己出发的边。为了能够在邻接链表中遍历到这三条边,就需要通过自己的指针先找到(1,3)这条边。然后根据1右侧的指针域,找到(1,2)这条边。然后再根据1右侧的指针域找到(0,1)这条边。对于C顶点来说,就需要通过自己的指针找到(1,2)这条边,然后根据2右侧的指针域找到(0,2)这条边。
构造过程的代码如下
public class GraphByAdjacencyMultiList<T> : IGraph<T>
{
private class Node<T>
{
public T data;
public Edge next;
public Node(T data)
{
this.data = data;
}
}
private class Edge
{
public int index1;
public Edge next1;
public int index2;
public Edge next2;
public int weight;
public Edge(int index1,int index2,int weight)
{
this.index1 = index1;
this.index2 = index2;
this.weight = weight;
}
}
private Node<T>[] _nodes;
private int _count;
public GraphByAdjacencyMultiList(int capacity)
{
_nodes = new Node<T>[capacity];
}
public void AddNode(T e)
{
_nodes[_count++] = new Node<T>(e);
}
public void AddEdge(int node1Index, int node2Index, int weight)
{
var edge = new Edge(node1Index, node2Index,weight);
edge.next1 = _nodes[node1Index].next;
_nodes[node1Index].next = edge;
edge.next2 = _nodes[node2Index].next;
_nodes[node2Index].next = edge;
}
}
五、边集数组
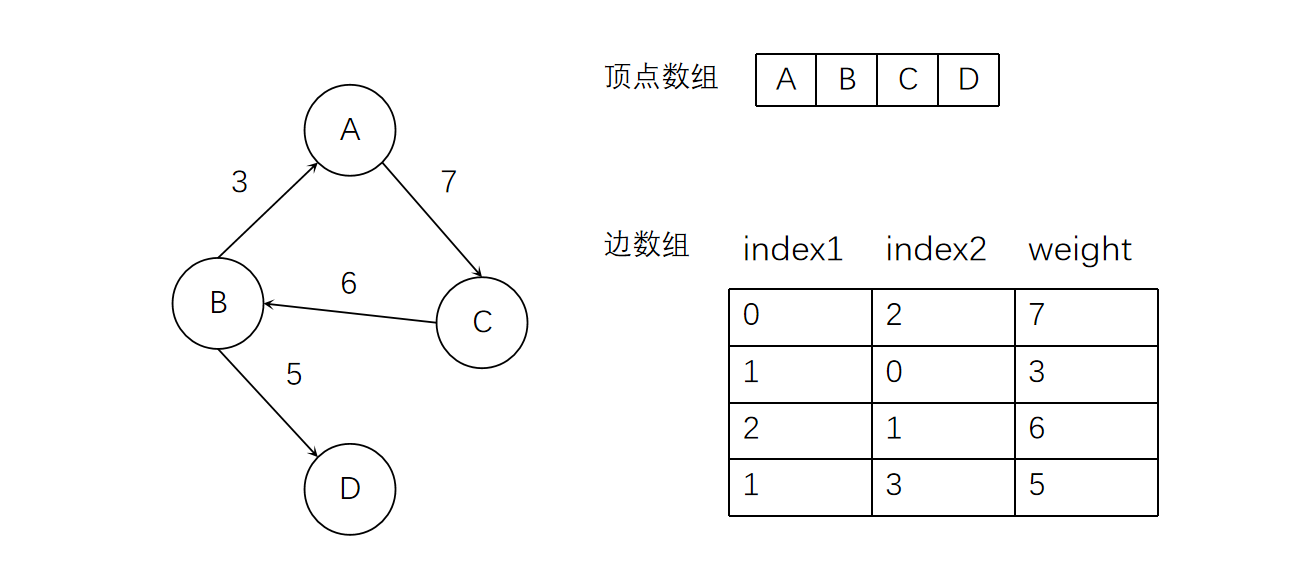
边集数组就比较简单了,它由两个一维数组组成。一个存储顶点信息,另一个存储边的信息。由于采用了一维数组,所以想要查询一个顶点的度就需要遍历整个数组,效率不高。但它本身就不是为了关注顶点相关的操作,而关注的是对边依次进行处理的操作。
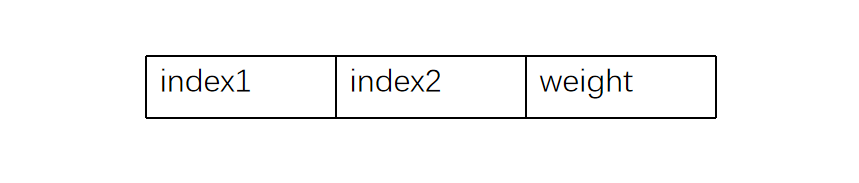
边集数组的边结构设计如下。index1和index2分别存储起止顶点下标,weight存储边的权值。
边集数组结构如下。很容易理解,这里不再赘述。
代码如下
public class GraphByEdgeCollectionArray<T> : IGraph<T>
{
private class Node<T>
{
public T data;
public Node(T data)
{
this.data = data;
}
}
private class Edge
{
public int index1;
public int index2;
public int weight;
public Edge(int index1,int index2,int weight)
{
this.index1 = index1;
this.index2 = index2;
this.weight = weight;
}
}
private Node<T>[] _nodes;
private List<Edge> _edges;
private int _count;
public GraphByEdgeCollectionArray(int capacity)
{
_nodes = new Node<T>[capacity];
_edges = new List<Edge>();
}
public void AddNode(T e)
{
_nodes[_count++] = new Node<T>(e);
}
public void AddEdge(int node1Index, int node2Index, int weight)
{
var edge = new Edge(node1Index, node2Index, weight);
_edges.Add(edge);
}
}
六、参考资料
[1].《大话数据结构》
[2]. https://blog.csdn.net/bible_reader/article/details/71250117