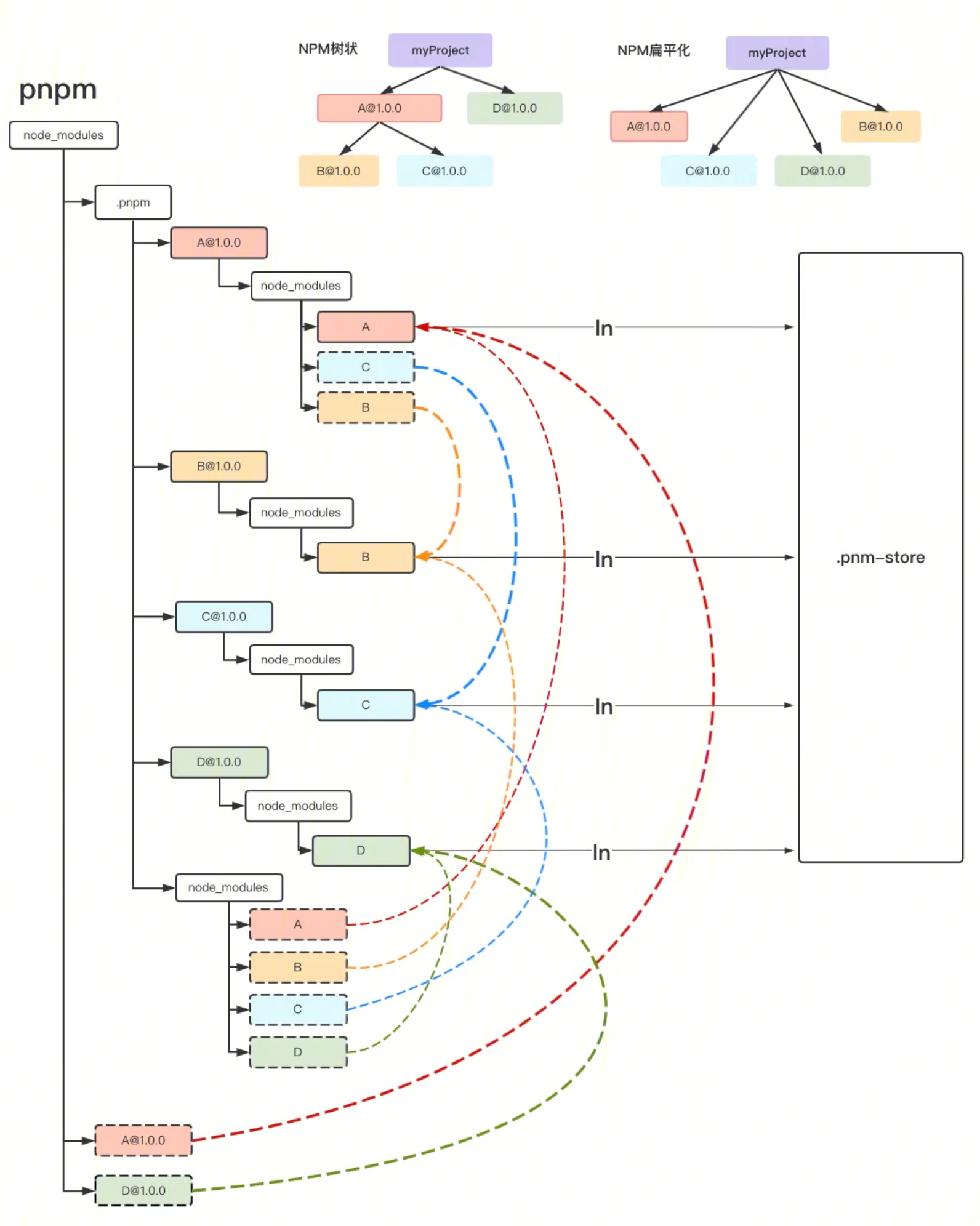
常见算法设计与分析的简单C++代码实现(排列、二分法搜索、Dijkstra算法、元素换位、单调子序列、硬币问题、运动员最佳匹配问题)
- 1 一些简单排列问题
- 2 二分法查找
- 3 前后元素换位
- 4 找最长单调递增子序列(O(n2)复杂度)
- 5最小硬币问题
- 一、问题描述:
- 二、实现目标:
- 三、 算法设计:
- 四、数据输入:
- 五、结果输出:
- 代码附录
- 6 Dijkstra算法实现
- 7运动员最佳配对问题
- 一、问题描述
- 二、算法设计
- 三、数据输入
- 四、结果输出及具体实现
Author(作者): Nirvana Of Phoenixl
*Proverbs for you(送给你的哦):There is no doubt that good things will always come, and when it comes late, it can be a surprise.如有转载请注明,谢谢!
1 一些简单排列问题
要求:求一组数的最大值,实现功能任意输入数字计算出其最大值,代码详情见附录:
实现过程截图如下图所示:
(1)输入数组直接求解最大值实现截图,如图1所示,完整实现代码详情见附录1:

图1 求数组最大值
附录1:
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
int max_n(int n, int num[]);
int max_2(int a, int b);
int main()
{
int max;
int num[4];
printf("Please input 4 numbers:");
scanf("%d %d %d %d", &num[0], &num[1], &num[2], &num[3]);
max = max_n(4, num);
printf("%d", max);
}
int max_n(int n, int num[])
{
int max;
if (n > 2)
max = max_2(num[n - 1], max_n(n - 1, num));
if (n == 2)
max = max_2(num[n - 2], num[n - 1]);
return max;
}
int max_2(int a, int b)
{
return (a > b ? a : b);
}
(2)利用递归法求最大值,如图2所示,限制数组长度,实现求解最大值截图,完整实现代码详情见附录2:
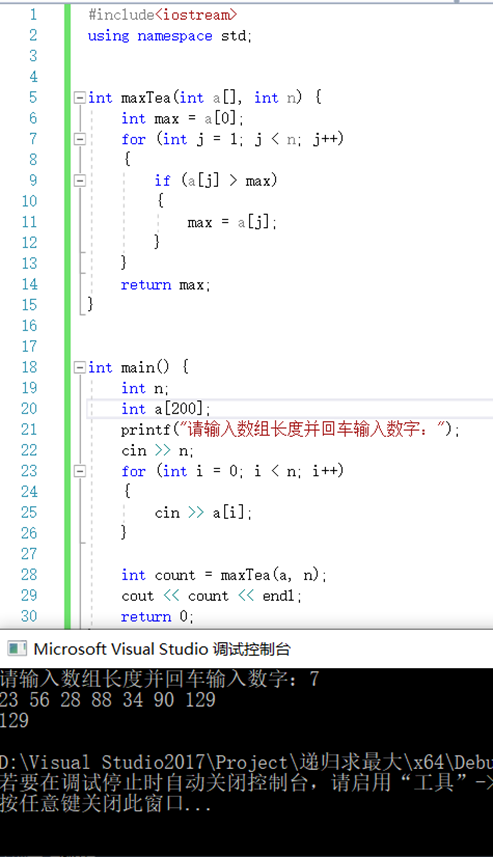
图2 递归法限制数组长度求最大值
附录2:
#include<iostream>
using namespace std;
int maxTea(int a[], int n) {
int max = a[0];
for (int j = 1; j < n; j++)
{
if (a[j] > max)
{
max = a[j];
}
}
return max;
}
int main() {
int n;
int a[200];
printf("请输入数组长度并回车输入数字:");
cin >> n;
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
int count = maxTea(a, n);
cout << count << endl;
return 0;
}
(3) 实现全排列问题(实现对输入任意数的全排列)
实现过程截图如图3所示,完整实现代码详情见附录3:
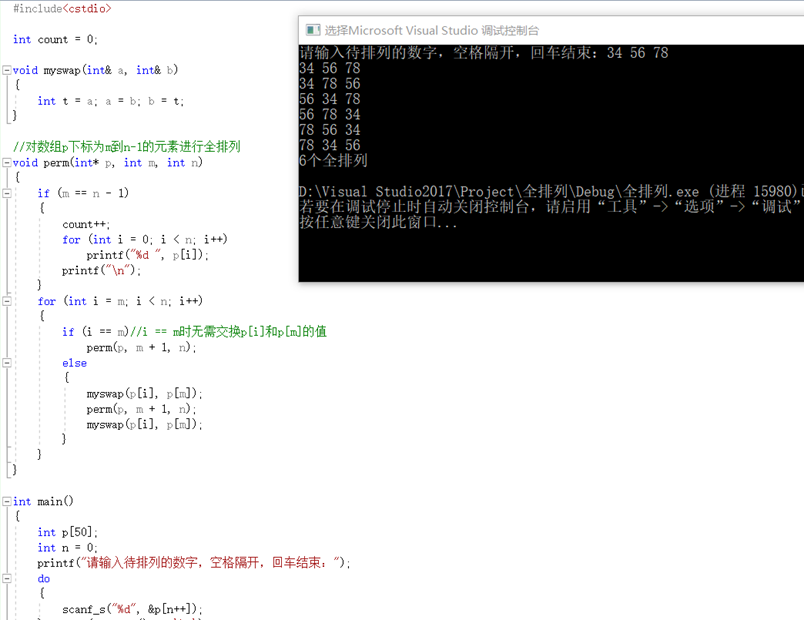
图3 任意输入数全排列实现
附录3:
#include<cstdio>
int count = 0;
void myswap(int& a, int& b)
{
int t = a; a = b; b = t;
}
//对数组p下标为m到n-1的元素进行全排列
void perm(int* p, int m, int n)
{
if (m == n - 1)
{
count++;
for (int i = 0; i < n; i++)
printf("%d ", p[i]);
printf("\n");
}
for (int i = m; i < n; i++)
{
if (i == m)//i == m时无需交换p[i]和p[m]的值
perm(p, m + 1, n);
else
{
myswap(p[i], p[m]);
perm(p, m + 1, n);
myswap(p[i], p[m]);
}
}
}
int main()
{
int p[50];
int n = 0;
printf("请输入待排列的数字,空格隔开,回车结束:");
do
{
scanf_s("%d", &p[n++]);
} while (getchar() != '\n');
perm(p, 0, n);
printf("%d个全排列\n", count);
return 0;
}
2 二分法查找
设a[0:n-1]是已排好序的数组。请改写二分搜索算法,使得当前搜索元素x不在数组中时,返回值小于x的最大元素位置i和大于x的最小元素位置j。当搜索元素在数组中时,i和j相同,均为x数组中的位置。实现过程部分截图如下所示:
(1)当x属于a[0:n-1]时,i和j均返回x元素的位置,如图1所示:
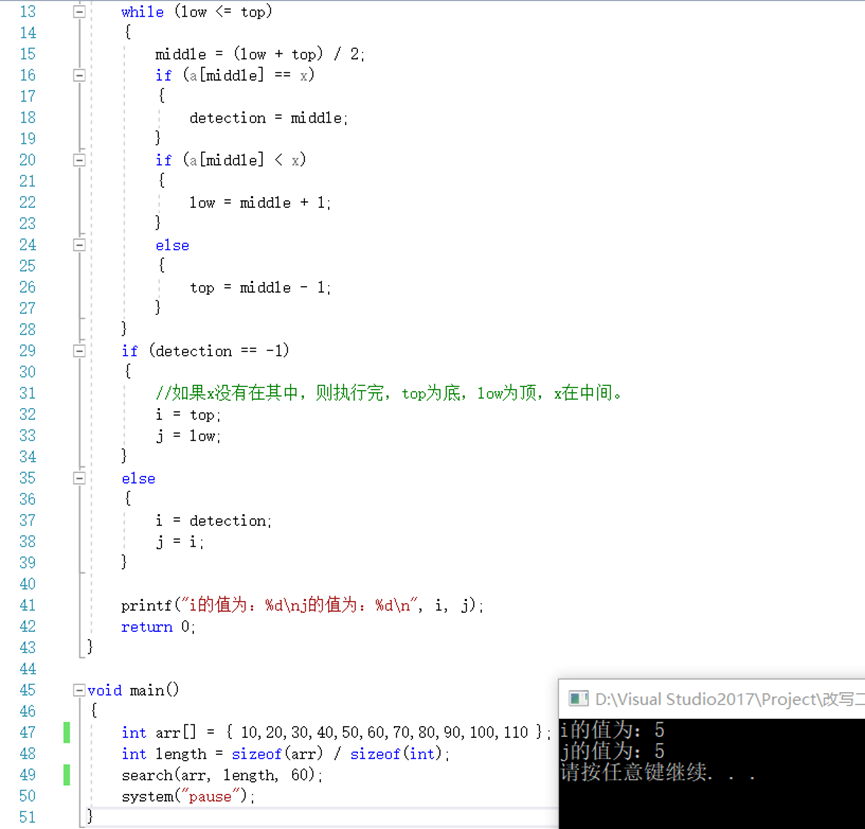
图1 x属于数组a[]
附录代码:
#include<stdio.h>
#include<stdlib.h>
//二分法查找
int search(int a[], int length, int x) //a是搜索数组,x为搜索元素
{
int i = 0, j = 0;
int detection = -1; //标志位
int top = length - 1; // 数组的右边界
int middle = 0; //中间值的下标
int low = 0; //数组的左边界
while (low <= top)
{
middle = (low + top) / 2;
if (a[middle] == x)
{
detection = middle;
}
if (a[middle] < x)
{
low = middle + 1;
}
else
{
top = middle - 1;
}
}
if (detection == -1)
{
//如果x没有在其中,则执行完,top为底,low为顶,x在中间。
i = top;
j = low;
}
else
{
i = detection;
j = i;
}
printf("i的值为:%d\nj的值为:%d\n", i, j);
return 0;
}
void main()
{
int arr[] = { 10,20,30,40,50,60,70,80,90,100,110 };
int length = sizeof(arr) / sizeof(int);
search(arr, length, 92);
system("pause");
}
(2) 当x不属于a[0:n-1]时,返回值小于x的最大元素位置i和大于x的最小元素位置j,如图2所示:

图2 x不属于数组a[]
3 前后元素换位
设a[0:n-1]是有n个元素的数组,k是一个非负整数。试着设计一个算法将子数组a[0:k-1]与a[k:n-1]换位。要求算法在最坏的情况下耗时O(n),且只用到O(1)的辅助空间。实现过程部分截图如图3所示:
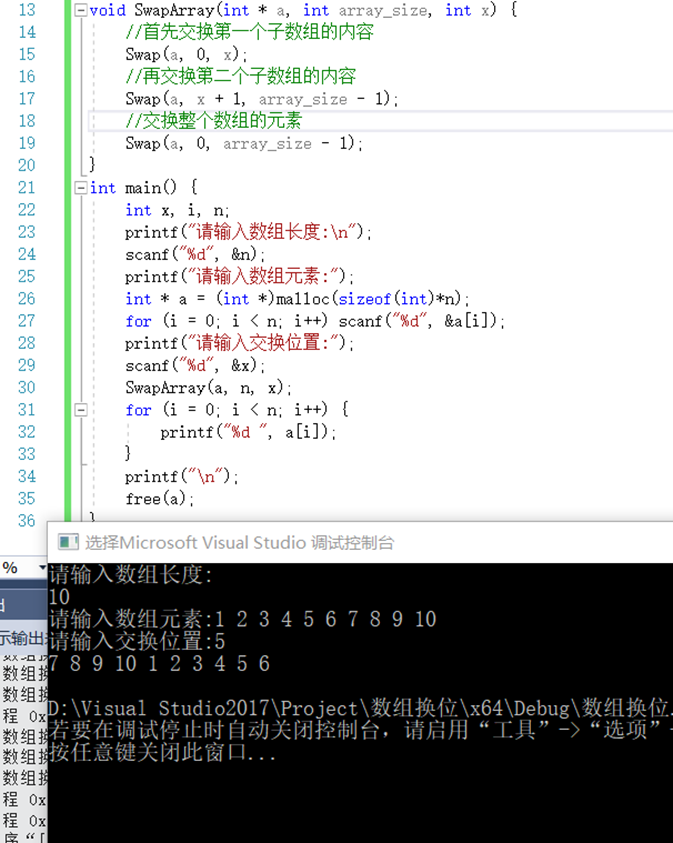
图3 数据交换
代码附录:
#pragma warning(disable:4996); // 解决报错
#include <stdio.h>
#include <stdlib.h>
void Swap(int * a, int left, int right) {
//交换数组left到right的内容
for (; left < right; left++, right--) {
int t = a[left];
a[left] = a[right];
a[right] = t;
}
}
void SwapArray(int * a, int array_size, int x) {
//首先交换第一个子数组的内容
Swap(a, 0, x);
//再交换第二个子数组的内容
Swap(a, x + 1, array_size - 1);
//交换整个数组的元素
Swap(a, 0, array_size - 1);
}
int main() {
int x, i, n;
printf("请输入数组长度:\n");
scanf("%d", &n);
printf("请输入数组元素:");
int * a = (int *)malloc(sizeof(int)*n);
for (i = 0; i < n; i++) scanf("%d", &a[i]);
printf("请输入交换位置:");
scanf("%d", &x);
SwapArray(a, n, x);
for (i = 0; i < n; i++) {
printf("%d ", a[i]);
}
printf("\n");
free(a);
}
4 找最长单调递增子序列(O(n2)复杂度)
设计一个O(n2)时间的算法,找出由n个数组成的序列的最长单调递增子序列。
实现过程及主要步骤:
1.输入一个序列a[]
2.将该序列进行排序得到新的序列b[](递增序列)
3.将问题转化为求这两个序列a,b的最大公共子序列
4.运用动态规划的解题思想,先求得子问题的结果,记录在c[][]数组中,再根据c[][]中的值的情况得到最大公共子序列。
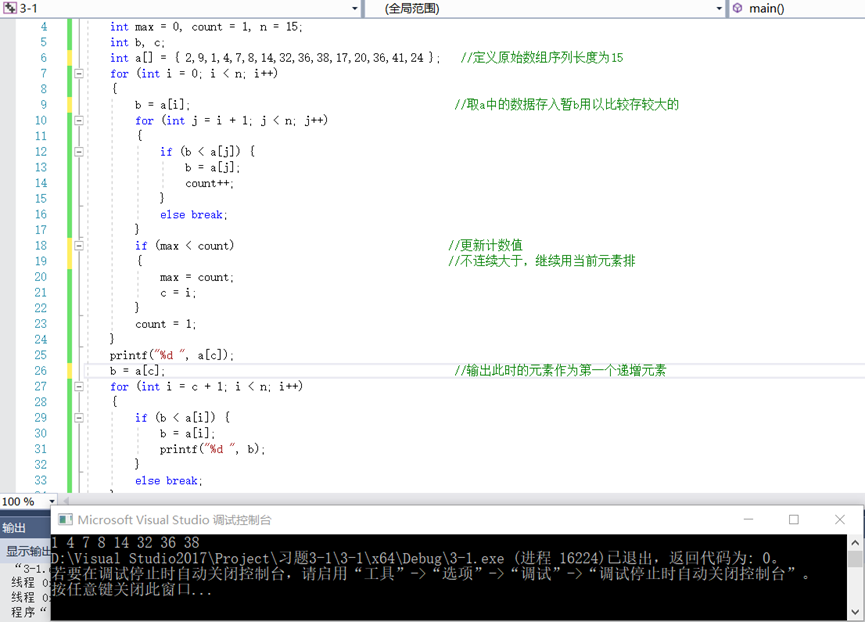
(代码见如下)
#include<stdio.h>
int main()
{
int max = 0, count = 1, n = 15;
int b, c;
int a[] = { 2,9,1,4,7,8,14,32,36,38,17,20,36,41,24 }; //定义原始数组序列长度为15
for (int i = 0; i < n; i++)
{
b = a[i]; //取a中的数据存入暂b用以比较存较大的
for (int j = i + 1; j < n; j++)
{
if (b < a[j]) {
b = a[j];
count++;
}
else break;
}
if (max < count) //更新计数值
{ //不连续大于,继续用当前元素排
max = count;
c = i;
}
count = 1;
}
printf("%d ", a[c]);
b = a[c]; //输出此时的元素作为第一个递增元素
for (int i = c + 1; i < n; i++)
{
if (b < a[i]) {
b = a[i];
printf("%d ", b);
}
else break;
}
return 0;
}
5最小硬币问题
一、问题描述:
设有n种不同面值的硬币,各硬币的面值存于数组T[1:n]中。现要用这些面值的硬币来找零钱。可以使用的各种面值的硬币个数存于数组Coins[1:n]中。
二、实现目标:
对任意钱数0≤m≤20001,设计一个用最少硬币找钱m的方法。
三、 算法设计:
对于给定的1≤n≤10,硬币面值数组T和可以使用的各种面值的硬币个数数组Coins,以及钱数m,0≤m≤20001,计算找钱m的最少硬币数。
四、数据输入:
由文件input.txt提供输入数据,文件的第1行中只有1个整数给出n的值,第二行起每一行2个数,分别是T[j]和Coins[j]。最后一行是要找的钱数m。
五、结果输出:
将计算出的最少硬币数输出到文件output.txt。问题无解时输出-1。
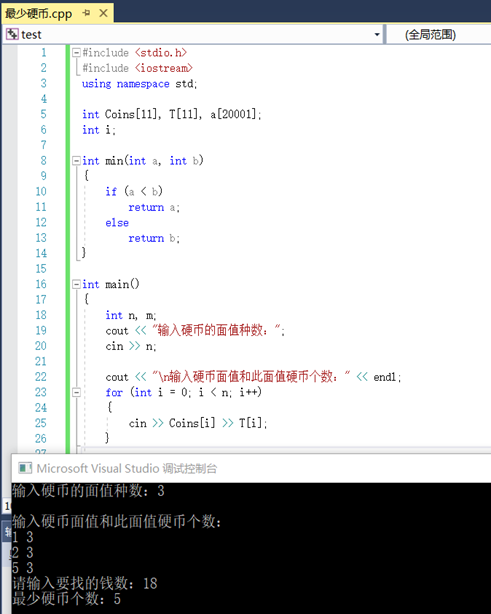
输出成功钱数m(18)对应最小硬币数
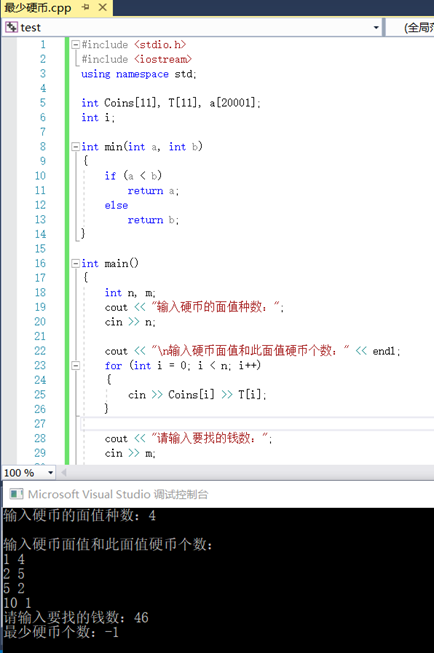
问题无解输出-1
实现过程截图:(具体代码实现详解见附录)
代码附录
#include <stdio.h>
#include <iostream>
using namespace std;
// cout<<a<<endl; 相当于printf("%d\n", a)
int Coins[11], T[11], a[20001]; //coins表示各硬币面值个数,T表示硬币面值,a表示钱数;
int i;
int min(int a, int b)
{
if (a < b)
return a;
else
return b;
}
int main()
{
int n, m;
cout << "输入硬币的面值种数:"; // 加载cout是一个iostream类的对象,向输出设备
cin >> n; //标准输入函数cin 它是代表标准的输入设备--键盘,也就是:cin >> 变量;
//输入多个变量可以写在一行,如:cin >> x >> y >> z;
cout << "\n输入硬币面值和此面值硬币个数:" << endl;
for (int i = 0; i < n; i++) //按照输入数面值数n,依次输入面值和数量
{
cin >> Coins[i] >> T[i];
}
cout << "请输入要找的钱数:";
cin >> m; //输入钱数m
for (i = 1; i <= m; i++)
a[i] = 99999;
for (i = 0; i < n; i++) // 在所有面值种类内循环,共计n种面值
{
for (int j = 1; j <= T[i]; j++) //从硬币面值数组中,依次取用所有面值硬币
{
for (int k = m; k >= Coins[i]; k--) //按照钱数m,从该面值对应的硬币数量中取
{
a[k] = min(a[k], a[k - Coins[i]] + 1);//
}
}
}
cout << "最少硬币个数:";
cout << (a[m] < m ? a[m] : -1) << endl;
}
cout << "最少硬币个数:";
cout << (a[m] < m ? a[m] : -1) << endl;
}
6 Dijkstra算法实现
点击这里_Dijkstra算法实现
本文由关于该算法的分析及实现,可以作为参考!
7运动员最佳配对问题
一、问题描述
羽毛球队员有男女运动员各n人。给定2个n×n矩阵P和Q。P[i][j]是男运动员i和女运动员j配对组合成混合双打的男运动员竞赛优势;Q[i][j]是女运动员i和男运动员j配合的女运动员竞赛优势。由于技术配合和心理状态等各种因素影响,P[i][j]不一定等于Q[j][i]。男运动员i和女运动员j配合组成混合双打的男女双方竞赛优势为P[i][j]*P[j][i]。设计一个算法,计算男女运动员最佳配对方法,使得各组男女双方竞赛优势的总和达到最大。
二、算法设计
设计一个算法,对于给定的男女运动员竞赛优势,计算男女运动员最佳配对法,使得各组男女双方竞赛优势的总和达到最大。
三、数据输入
由文件input.txt给出输入数据。第一行有1个正整数n。接下来的2n行,每行n个数;前n行是p,后n行是q。
四、结果输出及具体实现
将计算的男女双方竞赛优势的总和的最大值输出到文件output.txt。
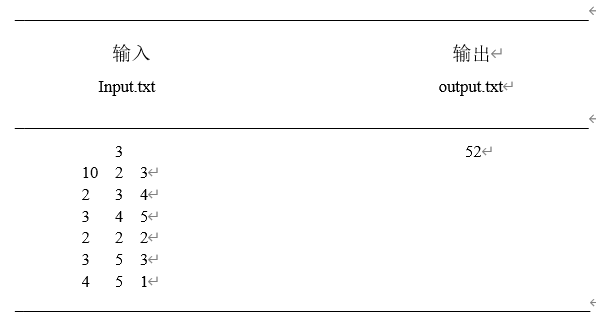
分析:对于给定的n来说,我们先确定男生的配对顺序是不变的,比如1,2,3等,从第1个男运动员开始搭配女运动员:第1个有n种搭配方法,第2个有n-1种搭配方法……第n个有n-(n-1)种搭配方法;根据问题给出的示例:输入n的值为3,表示男女运动员各有3名;
(1)根据男运动员A(1)、B(2)、C(3)按顺序搭配女运动员,他们分别对应的女运动员可以是:女运动员分别为1 2 3、1 3 2、2 1 3、2 3 1、3 1 2、3 2 1。
(2)确定该配对问题的解空间是{(1,2,3),(1,3,2),(2,1,3),(2,3,1),(3,1,2),(3,2,1)},整个问题可看成是1,2,3的全排列问题,将解空间组织成一棵排列树。
实现截图如下,代码实现见附录:
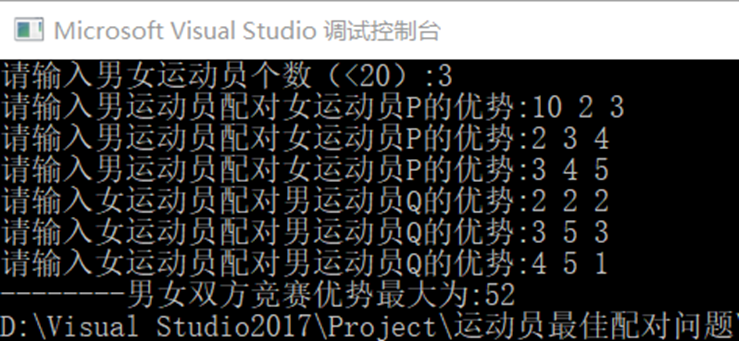
附录:
#include <iostream>
using namespace std;
int n, m[20][20], w[20][20]; // n表示男女生个数、用m表示男生,w表示女生
int sum = 0, a[20]; // sum表示配对总分数,a存入输入的男女运动员数
void Backtrack(int t) {
if (t > n) { //递归结束判定条件
int temp = 0;
for (int i = 0; i < n; i++) {
temp += m[a[i]][i] * w[i][a[i]]; //计算
}
if (temp > sum) {
sum = temp;
}
}
else {
for (int i = t; i <= n; i++) {
int temp = a[i - 1];
a[i - 1] = a[t - 1];
a[t - 1] = temp;
Backtrack(t + 1);
temp = a[i - 1];
a[i - 1] = a[t - 1];
a[t - 1] = temp;
}
}
}
int main() {
cout << "请输入男女运动员个数(<20):";
cin >> n;
for (int i = 0; i < n; i++) {
a[i] = i;
}
for (int i = 0; i < n; i++) {
cout << "请输入男运动员配对女运动员P的优势:";
for (int j = 0; j < n; j++) {
cin >> m[i][j];
}
}
for (int i = 0; i < n; i++) {
cout << "请输入女运动员配对男运动员Q的优势:";
for (int j = 0; j < n; j++) {
cin >> w[i][j];
}
}
Backtrack(1);
cout << "--------";
cout << "男女双方竞赛优势最大为:";
cout << sum;
return 0;
}