题目

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

解：

方法一

该题也是一题比较简单的动态规划问题，思路如下：

（1）当上楼梯的阶数n小于2时，直接return n，如n=0时一阶楼梯也不用上方法为0种。一阶楼梯时方法为1种。两阶楼梯时方法有两种，可以一次上两阶，也可以分开两次上一阶楼梯。

（2）当n>2时，我们可以发现，这时上楼梯的方法有多少种呢？我们可以一次上一阶也可以一次上两阶，设当前的阶级方法为dp[n]，那么为了到达n阶楼梯，它的上一步是怎么走的呢？如果它上一步是走了一阶楼梯，那么它上一步方法就是dp[n-1],如果它上一步是走了两阶楼梯，那么它上一步方法就是dp[n-2],这时动态规划就很明显了，它的方法数就是它上一步走一阶或者两阶方法数的总和：dp[n]=dp[n-1]+dp[n-2]。

class Solution {
    public int climbStairs(int n) {
  if(n<=2) return n;
  int []dp=new int[n+1];
  dp[0]=0;
  dp[1]=1;
  dp[2]=2;
  for(int i=3;i<=n;i++){
      dp[i]=dp[i-1]+dp[i-2];
  }
  return dp[n];
    }
}

用动态规划，时间复杂度和空间复杂度都是O(n)，中规中矩的表现。

方法二

看了力扣的题解这题有更好的做法，但需要较强的数学功底。有兴趣的小伙伴可以看一下。如果观察数学规律，可知本题是斐波那契数列，那么用斐波那契数列的公式即可解决问题，公式如下：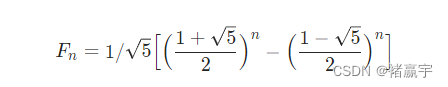

• 时间复杂度：O(logn)

class Solution {
    public int climbStairs(int n) {
        double sqrt_5 = Math.sqrt(5);
        double fib_n = Math.pow((1 + sqrt_5) / 2, n + 1) - Math.pow((1 - sqrt_5) / 2,n + 1);
        return (int)(fib_n / sqrt_5);
    }
}