系列文章目录
第1章 绪论
第2章 机器学习概述
第3章 线性模型
第4章 前馈神经网络
第5章 卷积神经网络
第6章 循环神经网络
第7章 网络优化与正则化
第8章 注意力机制与外部记忆
第9章 无监督学习
第10章 模型独立的学习方式
第11章 概率图模型
第12章 深度信念网络
第13章 深度生成模型
第14章 深度强化学习
第15章 序列生成模型
文章目录
- 系列文章目录
- 前言
- 6.1 给神经网络添加记忆
- 6.1.1 延时神经网络
- 6.1.2 自回归模型
- 6.1.3 非线性自回归模型
- 6.2 循环神经网络
- 6.2.1 网络结构
- 6.2.2 网络按时间展开
- 6.2.3 简单循环网络
- 6.2.4 图灵完备
- 6.2.5 应用
- 6.3 循环神经网络在机器学习中的应用
- 6.3.1 序列到类别
- 6.3.2 同步的序列到序列模式
- 6.3.3 异步的序列到序列模式
- 6.4 梯度
- 6.4.1 参数定义
- 6.4.2 梯度
- 6.4.3 长程依赖问题
- 6.5 GRU 与LSTM
- 6.5.1GRU(Gated Recurrent Unit)
- 6.5.2 LSTM(Long Short-Term Memory)
- 6.6 深层模型
- 6.7 图网络
- 6.7.1 递归神经网络
- 6.7.2 图网络
- 6.7 循环网络的应用
- 判断句子合理性 作词、作诗、机器的翻译、看图说话、写字、对话系统、
- 总结
前言
6.1 给神经网络添加记忆
6.1.1 延时神经网络
延时神经网络(Time Delay Neural Network,TDNN),即建立一个额外的延时单元,用来存储网络的历史信息(可以包括输入、输出、隐状态等)
h
t
(
l
)
=
f
(
h
t
(
l
−
1
)
,
h
t
−
1
(
l
−
1
)
,
…
h
t
−
K
(
l
−
1
)
)
h_t^{(l)}=f(h_t^{(l-1)},h_{t-1}^{(l-1)},…h_{t-K}^{(l-1)})
ht(l)=f(ht(l−1),ht−1(l−1),…ht−K(l−1))

6.1.2 自回归模型
自回归模型(Autoregressive Model,AR),一类时间序列模型,用变量的历史信息来预测自己。
y
t
=
w
0
+
∑
k
=
1
K
w
k
y
t
−
k
+
ϵ
t
y_t=w_0+\sum _{k=1}^K w_ky_{t-k}+\epsilon_t
yt=w0+k=1∑Kwkyt−k+ϵt
ϵ t \epsilon_t ϵt为第t个时刻的噪音
6.1.3 非线性自回归模型
有外部输入的非线性自回归模型(Nonlinear Autoregressive with Exogenous Inputs Model,NARX)
y
t
=
f
(
x
t
,
x
t
−
1
,
…
,
x
t
−
K
x
,
y
t
−
1
,
y
t
−
2
,
…
,
y
t
−
K
x
)
y_t=f(x_t,x_{t-1},…,x_{t-K_x},y_{t-1},y_{t-2},…,y_{t-K_x})
yt=f(xt,xt−1,…,xt−Kx,yt−1,yt−2,…,yt−Kx)
其中 f(⋅) 表示非线性函数,可以是一个前馈网络,
K
x
K_x
Kx和
K
y
K_y
Ky 为超参数

6.2 循环神经网络
6.2.1 网络结构
循环神经网络通过使用带自反馈的神经元,能够处理任意长度的时序数据。
h
t
=
f
(
h
t
−
1
,
x
t
)
h_t=f(h_{t-1},x_t)
ht=f(ht−1,xt)

- 循环神经网络比前馈神经网络更加符合生物神经网络的结构。
- 循环神经网络已经被广泛应用在语音识别、语言模型以及自然语言生成等任务上。
6.2.2 网络按时间展开

6.2.3 简单循环网络
状态更新:
h
t
=
f
(
U
h
t
−
1
+
W
x
t
+
b
)
h_t=f(Uh_{t-1}+Wx_{t}+b)
ht=f(Uht−1+Wxt+b)
一个完全连接的循环网络是任何非线性动力系统的近似器 。

6.2.4 图灵完备
图灵完备(Turing Completeness)是指一种数据操作规则,比如一种计算机编程语言,可以实现图灵机的所有功能,解决所有的可计算问题。

一个完全连接的循环神经网络可以近似解决所有的可计算问题。
6.2.5 应用
- 作为输入-输出映射的机器学习模型(本节主要关注这种情况)。
- 作为存储器中的联想记忆模型。
6.3 循环神经网络在机器学习中的应用
6.3.1 序列到类别
模型结构:
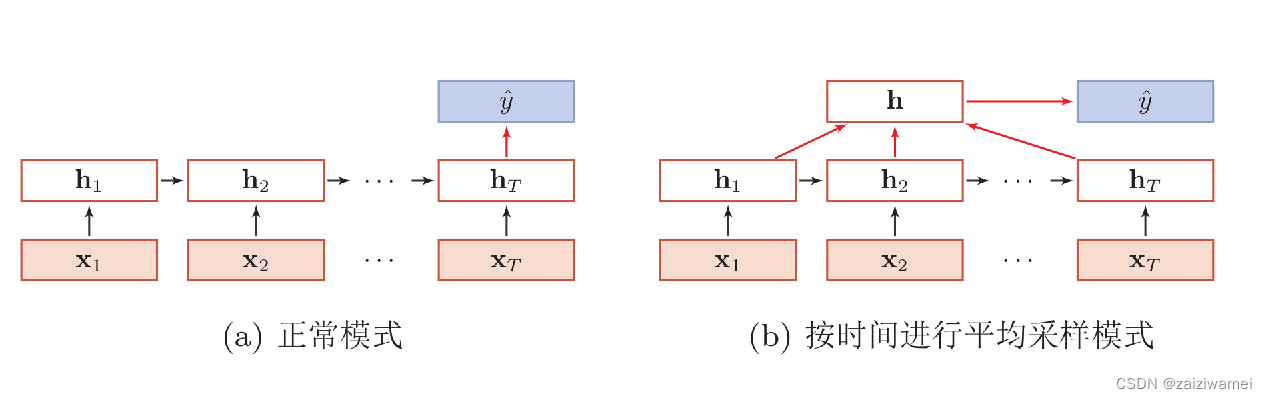
实际应用:

6.3.2 同步的序列到序列模式
模型结构:

实际应用:

从无结构的文本中抽取结构化的信息,形成知识。


6.3.3 异步的序列到序列模式
模型结构:

应用:

ϵ
t
\epsilon_t
ϵt为第t个时刻的噪音
6.4 梯度
6.4.1 参数定义
给定一个训练样本(x,y),其中x = (
x
1
x_{1}
x1,… ,
x
T
x_{T}
xT )为长度是T 的输入序列,y = (
y
1
y_{1}
y1 ,… ,
y
T
y_{T}
yT )是长度为T 的标签序列。则时刻t的瞬时损失函数为:
L
t
=
L
(
y
t
,
g
(
h
t
)
)
L_{t}=L(y_t,g(h_t))
Lt=L(yt,g(ht))
总损失函数为:
L
=
∑
t
=
1
T
L
t
L=\sum_{t=1}^{T}L_{t}
L=t=1∑TLt
6.4.2 梯度
随时间反向传播算法:


梯度消失与爆炸:

由于计算过程中
λ
\lambda
λ部分要经过多次求积,所以当得到的大于1时会出现梯度爆炸问题,小于1时会出现梯度消失问题。
6.4.3 长程依赖问题
出现原因:
循环神经网络在时间维度上非常深,所以会出现梯度消失或爆炸问题,因此实际上只能学习到短周期的依赖关系。这就是所谓的长程依赖问题。
改进原理:
针对梯度爆炸问题,可采用权重衰减或梯度截断方法;针对梯度消失问题,可改进模型。
改进方法
- 循环边改为线性依赖关系:
h t = h t − 1 + g ( x t ; θ ) h_t = h_{t-1}+g(x_t;\theta) ht=ht−1+g(xt;θ) - 增加非线性:
h t = h t − 1 + g ( x t ; h t − 1 ; θ ) h_t = h_{t-1}+g(x_t;h_{t-1};\theta) ht=ht−1+g(xt;ht−1;θ) - 使用门控制机:
控制信息的累计速度,包括有选择地加入新的信息,并由选择地遗忘之前累积的信息。
h t = h t − 1 + g ( x t ; h t − 1 ; θ ) h_t = h_{t-1}+g(x_t;h_{t-1};\theta) ht=ht−1+g(xt;ht−1;θ)
6.5 GRU 与LSTM
6.5.1GRU(Gated Recurrent Unit)
- 结构图

- 计算公式
r t = σ ( W r x t + U r h t − 1 + b r ) z t = σ ( W r x t + U z h t − 1 + b z ) h ~ t = t a n h ( W c x t + U ( r t ⊙ h t − 1 ) ) h t = z t ⊙ h t − 1 + ( 1 − z t ) ⊙ h ~ t r_t = \sigma(W_rx_t+U_rh_{t-1}+b_r) \\ z_t = \sigma(W_rx_t+U_zh_{t-1}+b_z)\\ \tilde h_t = tanh(W_cx_t+U(r_{t}\odot h_{t-1}))\\ h_t = z_t\odot h_{t-1}+(1-z_t)\odot \tilde h_t rt=σ(Wrxt+Urht−1+br)zt=σ(Wrxt+Uzht−1+bz)h~t=tanh(Wcxt+U(rt⊙ht−1))ht=zt⊙ht−1+(1−zt)⊙h~t
6.5.2 LSTM(Long Short-Term Memory)
-
结构图

-
计算公式
f t = σ ( W f x t + U f h t − 1 + b f ) i t = σ ( W i x t + U i h t − 1 + b i ) c ~ t = t a n h ( W c x t + U c h t − 1 + b c ) o t = σ ( W o x t + U o h t − 1 + b o ) c t = f t ⊙ c t − 1 + i t ⊙ c ~ t h t = o t ⊙ t a n h ( c t ) f_t = \sigma(W_fx_t+U_fh_{t-1}+b_f) \\ i_t = \sigma(W_ix_t+U_ih_{t-1}+b_i)\\ \tilde c_t = tanh(W_cx_t+U_ch_{t-1}+b_c)\\ o_t = \sigma(W_ox_t+U_oh_{t-1}+b_o) \\ c_t = f_t\odot c_{t-1}+i_t\odot \tilde c_t\\ h_t = o_t\odot tanh(c_t) ft=σ(Wfxt+Ufht−1+bf)it=σ(Wixt+Uiht−1+bi)c~t=tanh(Wcxt+Ucht−1+bc)ot=σ(Woxt+Uoht−1+bo)ct=ft⊙ct−1+it⊙c~tht=ot⊙tanh(ct) -
LSTM的各种变体

6.6 深层模型
堆叠循环神经网络:

双向循环神经网络:

6.7 图网络
6.7.1 递归神经网络
递归神经网络实在一个有向图无循环图上共享一个组合函数:

退化为循环神经网络:

自然语言的处理:

6.7.2 图网络
计算过程:

函数计算: