一、前言

最短路问题变化很多，不同数据范围的变化，也会导致算法运用的不同，下面给大家总结了不同最短路问题，不同数据范围应该用怎样的方式去解决。

二、算法讲解

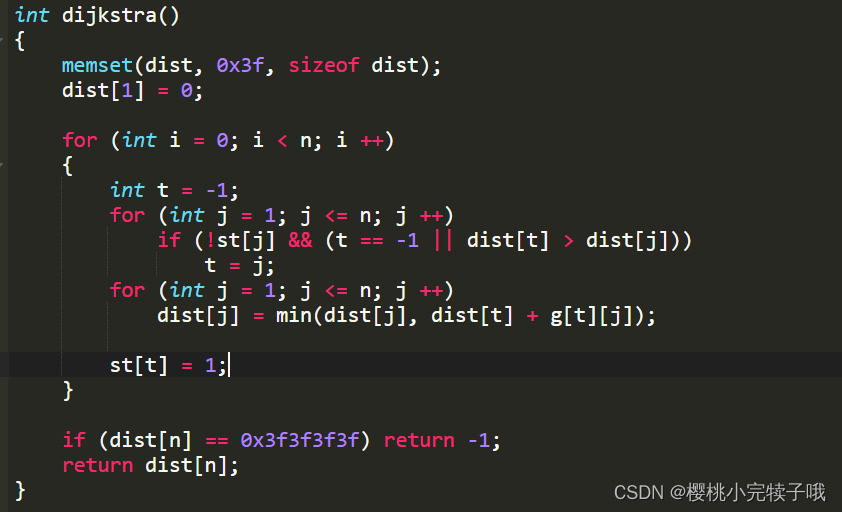
**1、Dijkstra--朴素算法：O(n * n)**

算法描述：

（1）初始化距离数组：dist[1] = 0, dist[i] = INF

（2）迭代n次，每次迭代确定一个min加入集合S（这里确定的min一定是上一次迭代所更新的所有邻边里的一条），n次迭代之后确定所有起点到所有点的最短距离

（3）将不在S集合中dist_min的点--->t

（4）t --->S

（5）用t更新到其他点的距离（相当于更新t的邻边）

算法简述：

简单来说，迭代后的效果就是利用每一次确定的一个点的最短距离，去更新他们的邻边的距离，n次迭代后，就确定了所有点到起点的最短距离。

适用范围：

适用于m >= n * n的无负权边的稠密图，用邻接矩阵存图。

代码实现：

2、Dijkstra--堆优化算法：O(mlogm)

算法描述：

（1）利用优先队列，代替朴素算法中找最小值那一步

（2）优先队列中存放两个关键字距离和起点

（3）每次取出堆顶元素，即所有待更新中距离的最小值

（4）更新前需要判断，该点是否已经确定过了最短距离，若确定了，则跳过，反之则进行更新操作

（5）更新后，再将所更新的邻边加入堆中

算法简述：

简单来说，每次遍历确定一个堆顶元素（所有边中的最短距离），利用已经确定了最短距离的点，去更新他们的邻边，将这些更新邻边放入队列中，直至堆中没有元素，即所有点到起点的最短距离已经确定

适用范围：

适用于 n = m的无负权边的稀疏图，用邻接表存图。

代码实现：

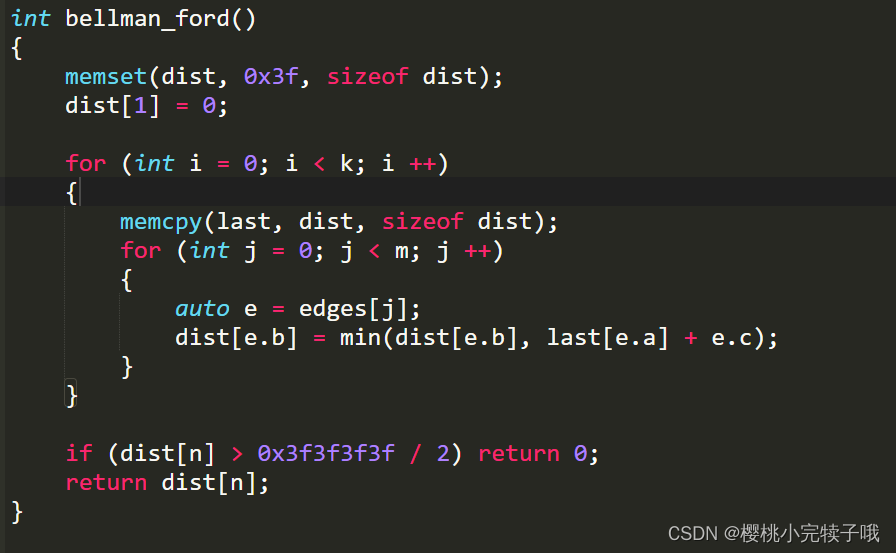
**3、Bellman_ford贝尔曼算法： O(n * m)**

算法描述：

（1）独特的存图方式 struct Edge{ int a, b, c;}edges[M];

（2）注意连锁想象需要备份

（3）初始化dist, 松弛dist[x.b] = min(dist[x.b], backup[x.a]+x.w);

（4）松弛k次，每次访问m条边

算法简述：

简单来说，经过k条边，循环k次，每次循环只会更新所有已经确定了的点的邻近的一条边，需要注意每一次循环利用上一次循环的结果，去更新本次循环的距离，所以需要备份

适用范围：

适用于有边数限制的最短路问题。

代码实现：

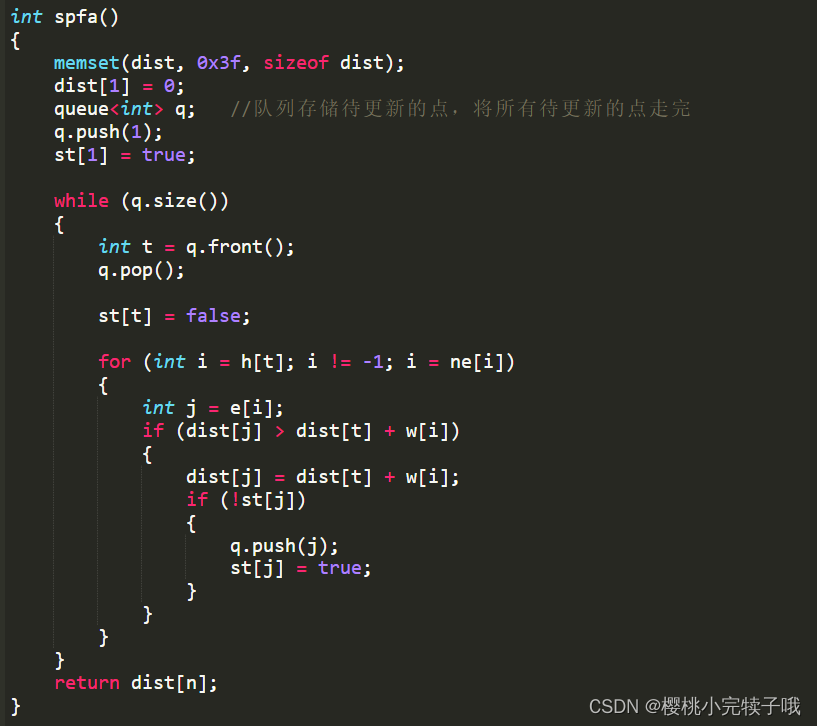
**4、Spfa算法：O(n * m)**

算法描述：

（1）利用队列优化贝尔曼算法中松弛一步进行优化

（2）将修改过最短距离的点加入队列中，因为修改了该点，其出边点的最短距离会变化，需要重新更新

（3）更新队列中当前点的所有出边

算法简述：

简单来说，就是将修改过了点，加入队列，用其重新更新其出边的点，直至队列中不存在值了，就说明所以点都找到了最短距离

适用范围：

n = m， 使用于存在负权边的稀疏图，用邻接表存

代码实现：

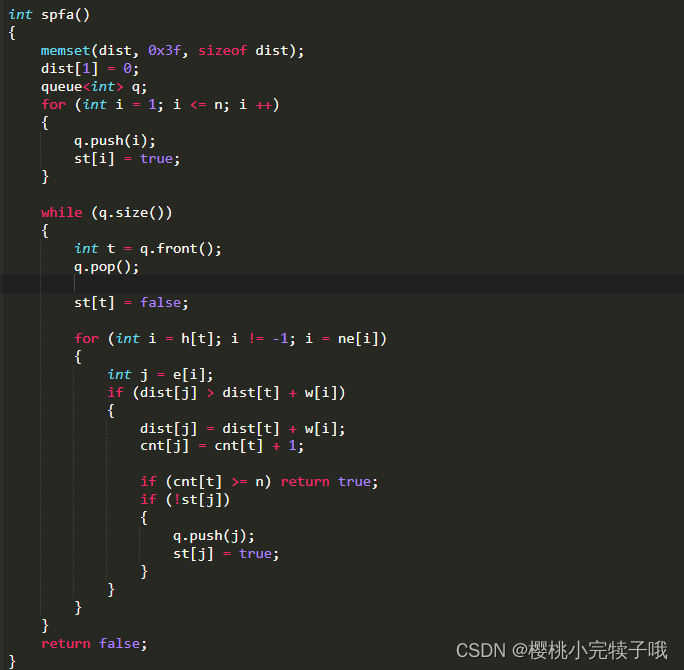
**5、Spfa处理负环：O(n * m)**

算法描述：

（1）若需要用来判断是否存在负环，则需要将所有的点都加入到队列中进行更新，因为可能起点1不在负环中

（2）在更新最短距离的同时，更新一下当前点的是第几次更新的结果，当前点的更新次数等于其入边的更新次数 + 1，即cnt[j] = cnt[t] + 1;

（3）判断当前点的更新次数有没有超过总点数n，超过了，说明有负权回路，即if (cnt[t] > n) return true;

算法简述：

简单来说，就是遍历所有的点，计数第i个点的最短距离是第几次更新得到的结果，如果是第n + 1及以上次更新得到，说明存在负权回路。

代码实现：

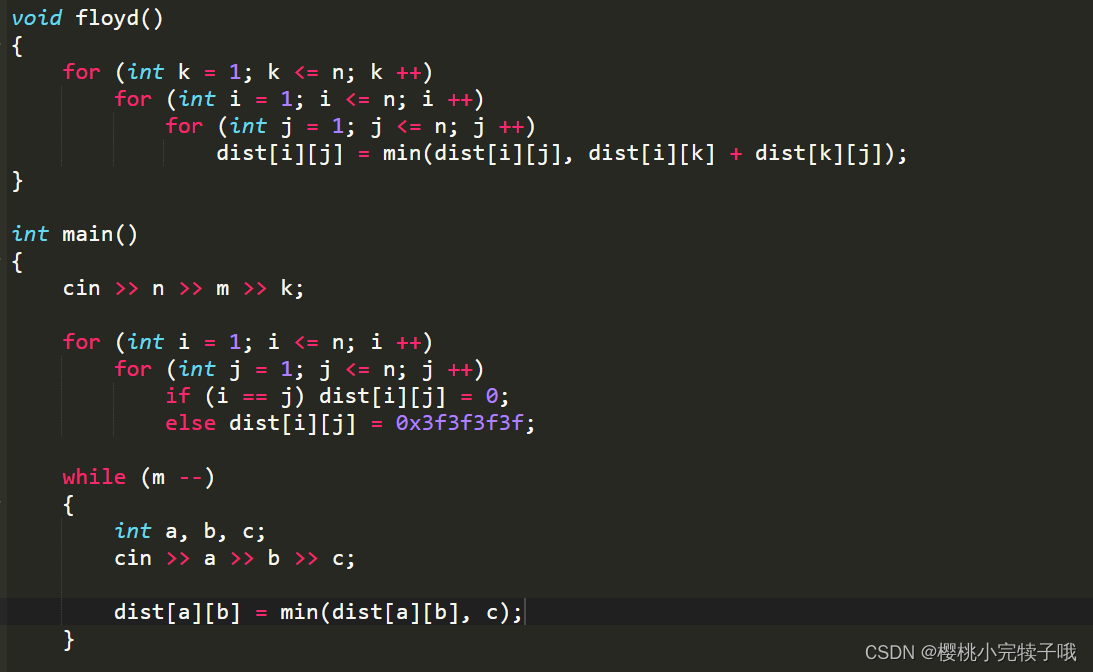
6、Floyd算法：O(n^3)

算法描述：

（1）独特初始化dist方式，如果i == j，则令其dist = 0，反之为 0x3f3f3f3f，这样可以处理自环问题，

（2）根据动态规划的思想，用三层循环更新dist

（3）循环k, i, j, dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);