周志华机器学习(6):支持向量机
- 6 支持向量机
- 6.1 间隔与支持向量
- 6.2 对偶问题(dual problem)
- 6.3 核函数
- 6.4 软间隔与正则化
基本是大段摘录加上一些自己的补充,去除了冗余的话。
6 支持向量机
6.1 间隔与支持向量
给定训练样本集
D
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
⋯
,
(
x
m
,
y
m
)
}
D=\{(\boldsymbol x_1,y_1),(\boldsymbol x_2,y_2),\cdots,(\boldsymbol x_m,y_m)\}
D={(x1,y1),(x2,y2),⋯,(xm,ym)},
y
∈
{
−
1
,
+
1
}
y\in\{-1,+1\}
y∈{−1,+1}, 分类学习最基本的想法就是基于训练集D在样本空间中找到一个划分超平面,将不同类别的样本分开。但能将训练样本分开的划分超平面可能有很多,所以应该努力去找划分结果最鲁棒的那个平面,也就是图6.1中中间那条加粗的。
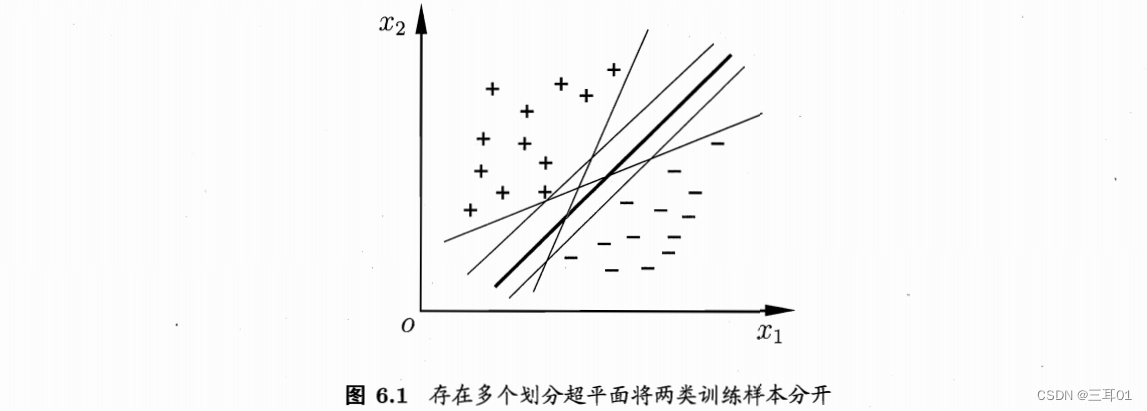
这张图中,两个轴
x
1
x_1
x1、
x
2
x_2
x2 是
x
\boldsymbol x
x 的属性,这里假定有两个属性。其实应该加上垂直于纸面表示标记的y轴,在这里,从y轴垂直往下看,y轴被压缩成了一个点。划分超平面公式:


如图6.2所示,距离超平面最近的这几个训练样本点使式(6.3)的等号成立,它们被称为“支持向量”(support vector),两个异类支持向量到超平面的距离之和为:
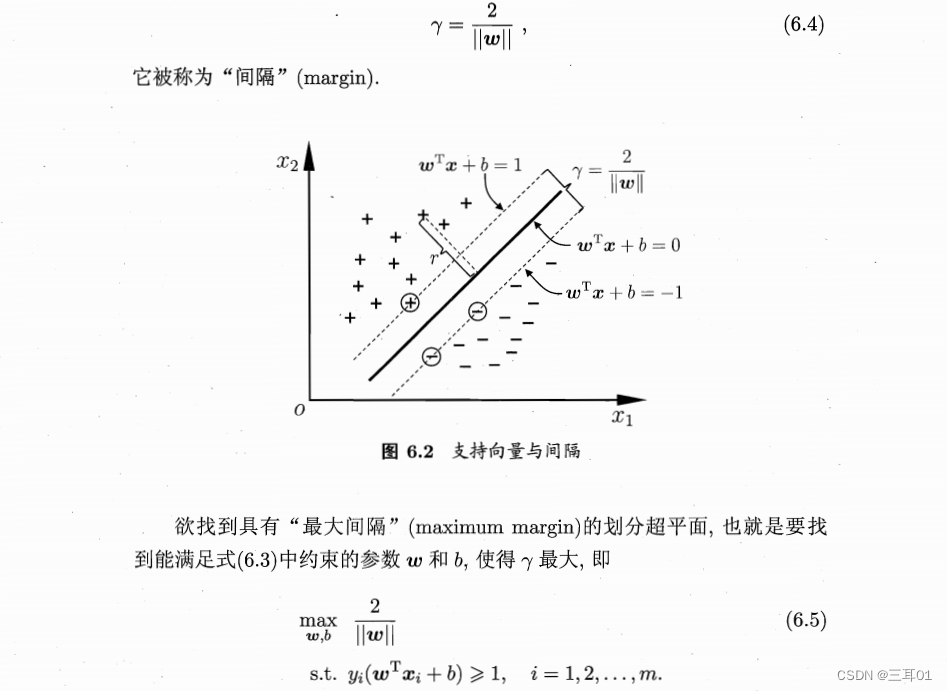
这个约束就是式(6.3)的变种。式(6.5)可以重写为:

6.2 对偶问题(dual problem)
拉格朗日:通过拉格朗日的办法重新定义一个无约束问题这个无约束问题等价于原来的约束优化问题,从而将约束问题无约束化。
如果原始问题求解棘手,在满足KKT的条件下用求解对偶问题来代替求解原始问题,使得问题求解更加容易。
对偶问题的上界在KKT条件下等于原始问题的下界,因为原问题求解太复杂,就可以在满足KKT条件下求解对偶问题。
拉格朗日对偶问题(Lagrange duality)
希望求解式(6.6),用拉格朗日乘子法得到其对偶问题,就是对每一个约束都添加拉格朗日乘子
α
i
≥
0
\alpha_i\geq 0
αi≥0,则拉格朗日函数为:


如何求解式(6.11)?——SMO(Sequential Minimal Optimization)

6.3 核函数
现实任务中,原始样本空间内也许并不存在一个能正确划分两类样本的超平面。
可将样本从原始空间映射到一个更高维的特征空间,使其在更高维特征空间内线性可分。
如果原始空间是有限维,即属性数有限,那么一定存在一个高维特征空间使样本可分。
在特征空间划分超平面对应的模型:



式(6.24)显示出模型最优解可通过训练样本的核函数展开,这一展式亦称“支持向量展式”(supportvector expansion). .
显然,若已知映射
ϕ
(
⋅
)
\phi(\cdot)
ϕ(⋅)的具体形式,则可写出核函数
κ
(
⋅
,
⋅
)
\kappa(\cdot,\cdot)
κ(⋅,⋅)。
但在现实任务中我们通常不知道
ϕ
(
⋅
)
\phi(\cdot)
ϕ(⋅)是什么形式,是否存在合适的核函数?什么样的函数能做核函数?定理如下:

核函数选择是SVM的最大变数,几种常用的核函数:

核函数还可以通过核函数的线性组合、直积、对核函数进行函数操作来得到。
6.4 软间隔与正则化
软间隔(soft margin):现实任务中很难有合适的核函数使得训练样本在特征空间中线性可分,即使有,也可能是过拟合。
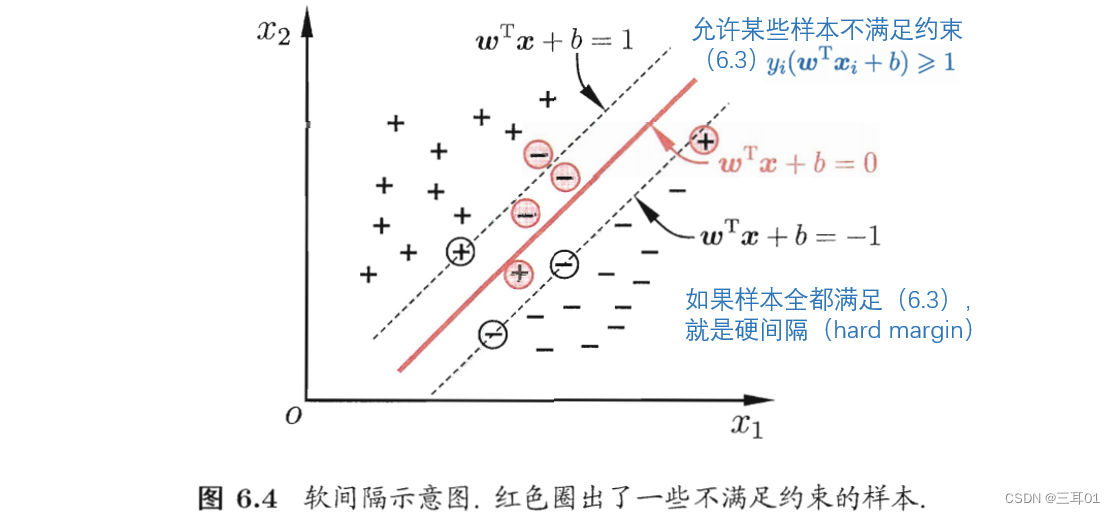
上图中(6.3)的约束被写为一个不等式,即为式(6.28)




还可以把式(6.29)中的0/1损失函数换成别的替代损失函数以得到其他学习模型,这些模型的性质与所用的替代函数直接相关: