线索二叉树

news2025/2/21 4:02:40

目录

一、线索二叉树的类型定义

 二、各种线索化的二叉树

 三、中序线索二叉树的算法

 完整代码：

一、线索二叉树的类型定义

typedef struct BTNode
{
    ElemType data;//数据域
    struct BTNode* lchild;//左孩子或线索指针
    struct BTNode* rchild;//右孩子或线索指针
    int ltag, rtag;
}BTNode, * BTree;
  •  左标志ltag=0，表示lchild指向左孩子结点；ltag=1，表示lchild指向前驱结点
  • 右标志rtag=0，表示rchild指向右孩子结点；rtag=1，表示rchild指向后继结点
  • 二叉树线索化的基本思想：
  • 二叉树的线索化实质上是遍历一棵二叉树。在遍历过程中，访问结点的操作是检查此结点的左、右指针域是否为空，如果为空，将它指向其前驱或后继结点的线索

 二、各种线索化的二叉树

 

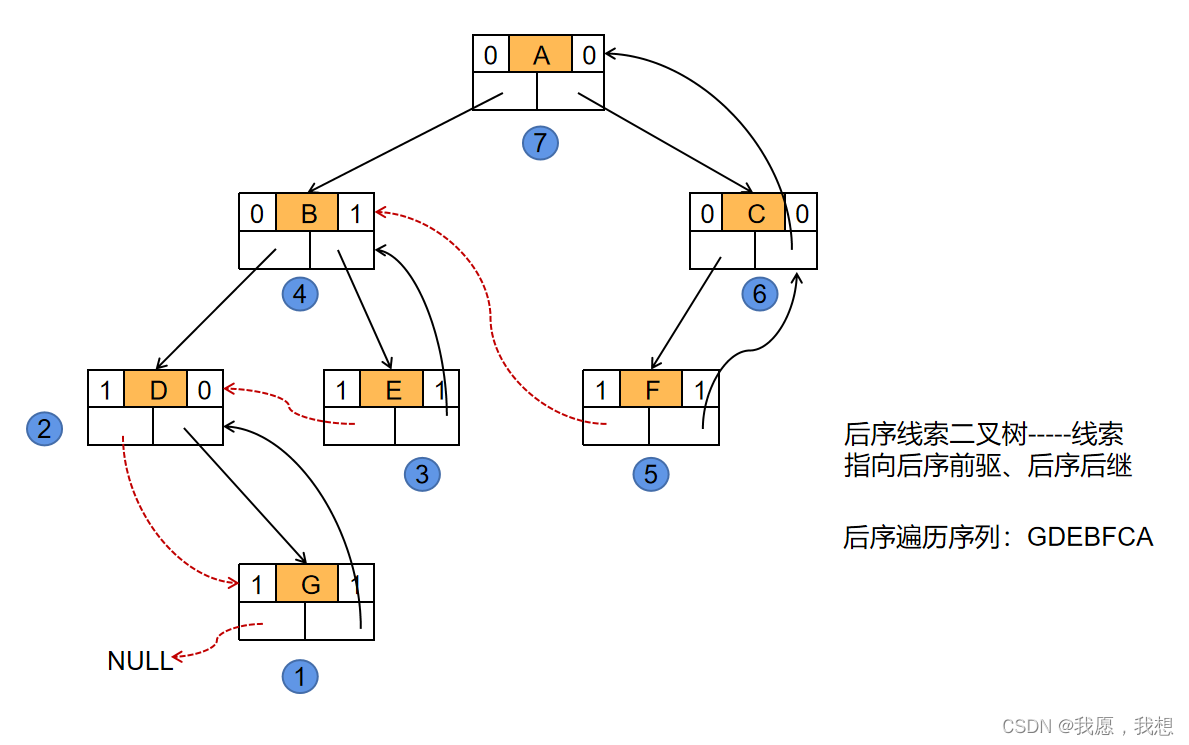
  •  为了操作方便，在存储线索二叉树的时候增设一个头结点，其结构与其他的线索二叉树的结点相同，只是数据域不存储任何数据，其左指针域指向二叉树的根结点，右指针指向遍历的最后一个结点，而二叉树在某种遍历下的第一个结点的前驱和最后一个结点的后继线索都指向头结点。

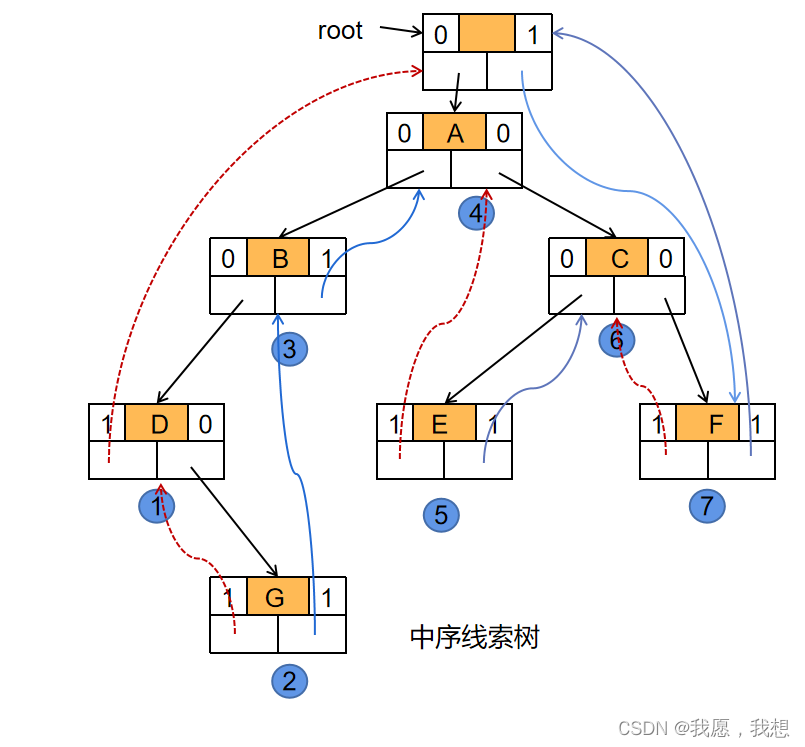
 三、中序线索二叉树的算法

  • 第一种方法建立并且遍历中序线索二叉树： 
//第一种方法
void CreatInThread(BTree &T);建立中序线索树
void InThread(BTree& T);//中序遍历二叉树，一边遍历一边线索化
void visit(BTree& q);//访问根结点
void visit2(BTree T);//遍历输出中序线索二叉树
BTNode* pre = NULL;//定义全局变量

void CreatInThread(BTree& T)//建立中序线索树
{
    pre = NULL;
    if (T != NULL)
    {
        InThread(T);//中序线索化二叉树
        if (pre!=NULL&&pre->rchild == NULL)
        {
            pre->rtag = 1;
        }
    }
}

void InThread(BTree& T)//中序遍历二叉树，一边遍历一边线索化
{
    if (T != NULL)
    {
        InThread(T->lchild);//左子树递归线索化
        visit(T);//访问根结点同时线索化
        InThread(T->rchild);//右子树递归线索化
    }
}

void visit(BTree& q)//访问根结点
{
    if (q->lchild == NULL)//左子树为空的时候，让其前驱线索指向空
    {
        q->lchild = pre;
        q->ltag = 1;
     }
    else
    {
        q->ltag = 0;
    }
    if (pre != NULL && pre->rchild == NULL)
    {
        pre->rchild = q;//建立前驱结点的后继线索（让前驱结点的rchild域存放后继结点的地址）
        pre->rtag = 1;
    }
    else
    {
        q->rtag = 0;
    }
    pre = q;
}

void visit2(BTree T)//遍历中序线索二叉树
{
    BTNode* p = T;
    while (p != NULL)
    {
        while (p->ltag == 0)//找开始结点
        {
            p = p->lchild;
        }
        cout << p->data << " ";//找到中序遍历最开始的结点并输出其data的值
        while (p->rtag == 1 && p->rchild != NULL)
        {
            p = p->rchild;
            cout << p->data << " ";
        }
        p = p->rchild;
    }
    return;
}
  •  第二种方法建立并且遍历中序线索二叉树：
//第二种方法
BTree CreatBTree(BTree& T);//中序线索化二叉树，先创建头结点root
void Thread(BTree& T);//中序线索化二叉树
void ThInOrder(BTree T);//在中序线索化二叉树中实现中序遍历（输出）
BTree CreatBTree(BTree & T)//中序线索化二叉树，先创建头结点root
{
    BTNode* root = (BTNode*)malloc(sizeof(BTNode));//创建一个头结点
    if (root == NULL)
    {
        exit(0);
    }
    root->ltag = 0;
    root->rtag = 1;
    root->rchild = T;
    if (T == NULL)//空二叉树
    {
        root->lchild = root;
    }
    else
    {
        root->lchild = T;//头结点的lchild域存放二叉树根结点的地址
        pre = root;
        Thread(T);//中序线索化二叉树
        pre->rchild = root;//最后处理加入头结点的线索
        pre->rtag = 1;
        root->rchild = pre;//头结点线索化

    }
    return root;
}

void Thread(BTree& T)//中序线索化二叉树
{
    if (T != NULL)
    {
        Thread(T->lchild);//左子树线索化
        if (T->lchild == NULL)
        {
            T->lchild = pre;//建立当前结点的前驱线索
            T->ltag = 1;
        }
        else
        {
            T->ltag = 0;
        }
        if (pre != NULL && pre->rchild == NULL)
        {
            pre->rchild = T;//建立前驱结点的后继线索
            pre->rtag = 1;
        }
        else
        {
            if (pre != NULL)
            {
                pre->rtag = 0;
            }
        }
        pre = T;
        Thread(T->rchild);//右子树线索化
    }
}


void ThInOrder(BTree tb)//tb指向中序线索二叉树的头结点
{
    BTNode* p = tb->lchild;
    while (p != tb)
    {
        while (p->ltag == 0)//找中序二叉树的开始结点（开始结点在最左下方）
        {
            p = p->lchild;
        }
        cout << p->data << " ";
        while (p->rtag == 1 && p->rchild != tb)
            //p->rtag=1并且p->rchild!=头结点表示p结点的rchild域存放的是中序遍历的后继结点的地址（线索）
        {
            p = p->rchild;//沿右线索访问后继结点
            cout << p->data << " ";
        }
        p = p->rchild;//转向p的右子树
    }
       
    
}

  •  完整代码：

#pragma once
#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<malloc.h>
using namespace std;
#define MAXSIZE 100
typedef char ElemType;
typedef struct BTNode
{
    ElemType data;//数据域
    struct BTNode* lchild;//左孩子或线索指针
    struct BTNode* rchild;//右孩子或线索指针
    int ltag, rtag;
}BTNode, * BTree;
 
BTree Creat(char str[]);//先序序列建立二叉链表

void PreOrder(BTree T);//先序遍历
void InOrder(BTree T);//中序遍历
void PostOrder(BTree T);//后序遍历
void LevelOrder(BTree T);//层序遍历


//第一种方法
void CreatInThread(BTree &T);建立中序线索树
void InThread(BTree& T);//中序遍历二叉树，一边遍历一边线索化
void visit(BTree& q);//访问根结点
void visit2(BTree T);//遍历输出中序线索二叉树


//第二种方法
BTree CreatBTree(BTree& T);//中序线索化二叉树，先创建头结点root
void Thread(BTree& T);//中序线索化二叉树
void ThInOrder(BTree T);//在中序线索化二叉树中实现中序遍历（输出）

//找后继结点
bool InPostNode(BTree& s);//寻找中序线索二叉树的的后继结点

#include"TBTree.h"
BTree Creat(char str[])//先序序列建立二叉链表（方法1）
{
    BTree T;
    static int i = 0;
    ElemType c = str[i++];
    if (c == '#')//输入#表示此结点下不存在分支
    {
        T = NULL;
    }
    else
    {
        T = (BTree)malloc(sizeof(BTree));
        if (T == NULL)
        {
            exit(0);
        }
        T->data = c;
        T->lchild = Creat(str);//递归创建左子树
        T->rchild = Creat(str);//到上一个结点的右边递归创建左右子树
    }
    return T;
}

BTNode* pre = NULL;//定义全局变量

void CreatInThread(BTree& T)//建立中序线索树
{
    pre = NULL;
    if (T != NULL)
    {
        InThread(T);//中序线索化二叉树
        if (pre!=NULL&&pre->rchild == NULL)
        {
            pre->rtag = 1;
        }
    }
}

void InThread(BTree& T)//中序遍历二叉树，一边遍历一边线索化
{
    if (T != NULL)
    {
        InThread(T->lchild);//左子树递归线索化
        visit(T);//访问根结点同时线索化
        InThread(T->rchild);//右子树递归线索化
    }
}

void visit(BTree& q)//访问根结点
{
    if (q->lchild == NULL)//左子树为空的时候，让其前驱线索指向空
    {
        q->lchild = pre;
        q->ltag = 1;
     }
    else
    {
        q->ltag = 0;
    }
    if (pre != NULL && pre->rchild == NULL)
    {
        pre->rchild = q;//建立前驱结点的后继线索（让前驱结点的rchild域存放后继结点的地址）
        pre->rtag = 1;
    }
    else
    {
        q->rtag = 0;
    }
    pre = q;
}

bool InPostNode(BTree& s)//寻找中序线索二叉树的的后继结点
{
    BTNode* post;
    post = s->rchild;
    if (s->rtag != 1)//结点s有右孩子
    {
        while (post->ltag == 0)//从右子树的根结点开始，沿左指针域往下查找，
            //直到没有左孩子为止
        {
            post = post->lchild;
        }
    }
    s = post;
    return true;
}


void visit2(BTree T)//遍历中序线索二叉树
{
    BTNode* p = T;
    while (p != NULL)
    {
        while (p->ltag == 0)//找开始结点
        {
            p = p->lchild;
        }
        cout << p->data << " ";//找到中序遍历最开始的结点并输出其data的值
        while (p->rtag == 1 && p->rchild != NULL)
        {
            p = p->rchild;
            cout << p->data << " ";
        }
        p = p->rchild;
    }
    return;
}





BTree CreatBTree(BTree & T)//中序线索化二叉树，先创建头结点root
{
    BTNode* root = (BTNode*)malloc(sizeof(BTNode));//创建一个头结点
    if (root == NULL)
    {
        exit(0);
    }
    root->ltag = 0;
    root->rtag = 1;
    root->rchild = T;
    if (T == NULL)//空二叉树
    {
        root->lchild = root;
    }
    else
    {
        root->lchild = T;//头结点的lchild域存放二叉树根结点的地址
        pre = root;
        Thread(T);//中序线索化二叉树
        pre->rchild = root;//最后处理加入头结点的线索
        pre->rtag = 1;
        root->rchild = pre;//头结点线索化

    }
    return root;
}

void Thread(BTree& T)//中序线索化二叉树
{
    if (T != NULL)
    {
        Thread(T->lchild);//左子树线索化
        if (T->lchild == NULL)
        {
            T->lchild = pre;//建立当前结点的前驱线索
            T->ltag = 1;
        }
        else
        {
            T->ltag = 0;
        }
        if (pre != NULL && pre->rchild == NULL)
        {
            pre->rchild = T;//建立前驱结点的后继线索
            pre->rtag = 1;
        }
        else
        {
            if (pre != NULL)
            {
                pre->rtag = 0;
            }
        }
        pre = T;
        Thread(T->rchild);//右子树线索化
    }
}


void ThInOrder(BTree tb)//tb指向中序线索二叉树的头结点
{
    BTNode* p = tb->lchild;
    while (p != tb)
    {
        while (p->ltag == 0)//找中序二叉树的开始结点（开始结点在最左下方）
        {
            p = p->lchild;
        }
        cout << p->data << " ";
        while (p->rtag == 1 && p->rchild != tb)
            //p->rtag=1并且p->rchild!=头结点表示p结点的rchild域存放的是中序遍历的后继结点的地址（线索）
        {
            p = p->rchild;//沿右线索访问后继结点
            cout << p->data << " ";
        }
        p = p->rchild;//转向p的右子树
    }
       
    
}

void PreOrder(BTree T)//先序遍历
{
    if (T != NULL)
    {
        cout << T->data << " ";//访问根结点
        PreOrder(T->lchild);//先序遍历左子树
        PreOrder(T->rchild);//先序遍历右子树
    }
}

void InOrder(BTree T)//中序遍历
{
    if (T != NULL)
    {
        InOrder(T->lchild);
        cout << T->data << " ";
        InOrder(T->rchild);
    }

}
void PostOrder(BTree T)//后序遍历
{
    if (T != NULL)
    {
        PostOrder(T->lchild);
        PostOrder(T->rchild);
        cout << T->data << " ";
    }
}


void LevelOrder(BTree T)//层序遍历
{
    BTNode* p;
    BTNode* qu[MAXSIZE];//定义循环队列，存放结点指针
    int front, rear;//定义头指针和尾指针
    front = rear = 0;//置队列为空队列
    rear++;
    qu[rear] = T;//根结点指针进队
    rear++;//队尾指针指向队尾元素的后一个位置
    front = (front + 1) % MAXSIZE;//队头指针加1取模
    while (front != rear)//队列不为空
    {
        p = qu[front];//取队头元素
        front = (front + 1) % MAXSIZE;//队头元素出队，队头指针后移
        cout << p->data << " ";
        if (p->lchild != NULL)
        {
            qu[rear] = p->lchild;//p结点的左孩子进栈
            rear = (rear + 1) % MAXSIZE;//队尾指针加1取模
        }
        if (p->rchild != NULL)
        {
            qu[rear] = p->rchild;//p结点的右孩子进栈
            rear = (rear + 1) % MAXSIZE;
        }
    }
}

#include"TBTree.h"

int main()
{
	cout << "二叉树建立的第一种方法" << endl;
	BTree T;//T为指向根结点的指针
	T = (BTree)malloc(50*sizeof(BTree));
	char str[] = { 'a','b','d','#','g','#','#','#','c','e','#','#','f','#','#' };
	T = Creat(str);
	cout << "先序遍历结果：";
	PreOrder(T);//先序遍历
	cout << endl;
	cout << "中序遍历结果：";
	InOrder(T);//中序遍历
	cout << endl;
	cout << "后序遍历结果：";
	PostOrder(T);//后序遍历
	cout << endl;
	cout << "层次遍历的结果：";
	LevelOrder(T);
	cout << endl << endl;


	/*cout << "中序线索树遍历结果：";
	CreatInThread(T);
	visit2(T);
	cout << endl << endl;*/


	cout << "中序遍历结果2：";
	BTree tb;
	tb = (BTree)malloc(50*sizeof(BTree));

	tb = CreatBTree(T);
	ThInOrder(tb);
	//system("pause");
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/29009.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

锐捷MPLS隧道单域实验配置

锐捷MPLS隧道单域实验配置

目录 配置AS100内的IGP路由协议 配置AS内的LDP 配置PE-PE的MP-BGP协议 在PE侧配置PE-CE的路由协议 在CE侧配置PE-CE的路由协议 将CE的路由重发布进MP-BGP中 将MP-BGP的路由重发布进CE中 MPLS隧道——单域基础理论讲解_静下心来敲木鱼的博客-CSDN博客_mpls隧道https://bl…
阅读更多...
Python安装

Python安装

一、官网下载 二、安装 找到下载的安装包&#xff0c;直接双击安装 三、设置环境变量 1、mac自带的python版本 2、修改为新下载的python3.11版本 1&#xff09;修改.bash_profile vi ~/.bash_profile 修改完成后&#xff0c;生效该文件&#xff1a;source ~/.bash_profile…
阅读更多...
如何写出公众号爆文？分享你一份爆文写作秘籍

如何写出公众号爆文？分享你一份爆文写作秘籍

新媒体时代&#xff0c;想要产出一篇公众号爆文真的是难于上青天&#xff01;现在公众号内容同质化严重&#xff0c;如果你没有一些新颖的观点和真本事&#xff0c;是无法从成千上万的公众号中脱颖而出的&#xff01; 如何写出公众号爆文&#xff1f;为什么你看了那么多写作干货…
阅读更多...
java--07 面向对象

java--07 面向对象

altenter 文件名和public名保持一致 两个变量指向同一个对象的内存图&#xff1a;如果被一个对象更改 &#xff0c;另外一个对象跟着更改 垃圾回收机制&#xff1a; altenter &#xff1a;添加方法 ctraltt:添加循环 构造器 this关键字 ​​​​​​​ 封装&#x…
阅读更多...
周志华机器学习（6）：支持向量机

周志华机器学习（6）：支持向量机

周志华机器学习&#xff08;6&#xff09;&#xff1a;支持向量机6 支持向量机6.1 间隔与支持向量6.2 对偶问题&#xff08;dual problem&#xff09;6.3 核函数6.4 软间隔与正则化基本是大段摘录加上一些自己的补充&#xff0c;去除了冗余的话。6 支持向量机 6.1 间隔与支持向…
阅读更多...
实体店应该围绕什么核心来打造自己体系多模式多平台的生态

实体店应该围绕什么核心来打造自己体系多模式多平台的生态

大家好&#xff0c;我是阿璋&#xff0c;阿璋时不时会发布一些创新的电商资讯&#xff0c;经过电商与疫情的反复摧残&#xff0c;实体商家的收益大不如从前&#xff0c;营业额一跌再跌&#xff0c;迎来实体寒潮&#xff0c;本期给大家分享一个实体店结合共享消费积分联盟广告生…
阅读更多...
封神之作，超火Java面试突击手册，进大厂真的就这么简单？

封神之作，超火Java面试突击手册，进大厂真的就这么简单？

2022年的互联网行业竞争越来越严峻&#xff0c;面试也是越来越难&#xff0c;一直以来我都想整理一套完美的面试宝典&#xff0c;奈何难抽出时间&#xff0c;这套完整的java后端学习路线以及1000道的Java面试手册我整理了整整1个月&#xff0c;上传到Git上目前star数达到了30K …
阅读更多...
MCE | 阿尔兹海默症发病机制

MCE | 阿尔兹海默症发病机制

阿尔兹海默症 (Alzheimers Disease, AD)&#xff0c;俗语常说的“老年痴呆症”&#xff0c;在奥斯卡提名短片《勿忘我》中以动画形式展现出了阿尔兹海默症患者的世界&#xff0c;动画中的老人&#xff0c;逐渐失去自己的记忆&#xff0c;甚至忘记最爱的人&#xff0c;他的脑海中…
阅读更多...
学习软件测试需要注意的几点

学习软件测试需要注意的几点

⒈ 测试主页技能掌握 关于软件测试&#xff0c;所需要的专业技能&#xff1a; l 基础测试技术&#xff1a;黑盒测试、白盒测试、测试用例设计等; l 软件测试方法&#xff1a;单元测试、功能测试、集成测试、系统测试、性能测试; l 软件测试知识&#xff1a;基础的测试流程管理、…
阅读更多...
孩子没有感统失调的表现，还有必要做感统训练吗？

孩子没有感统失调的表现，还有必要做感统训练吗？

孩子没有感统失调表现&#xff0c;是不是就可以放心了&#xff1f; 孩子训练一段时间&#xff0c;进步非常大&#xff0c;是不是就不需要再继续做训练了&#xff1f; 答案是&#xff1a;无论孩子能力发展如何&#xff0c;感统训练都必不可少。 为什么每个孩子都需要感统训练…
阅读更多...
Git——IDEA集成GitHub详细操作

Git——IDEA集成GitHub详细操作

目录 一、 设置GitHub账号 二、分享项目到GitHub 三、push推送本地库到远程库 3.1 第一种方法&#xff1a; 3.2 第二种方法&#xff1a;SSH 四、pull拉取远程库到本地库 五、clone克隆远程库到本地 一、 设置GitHub账号 可以使用下面这个token登录&#xff0c;第一个太慢太慢…
阅读更多...
CodeBlocks C++开发环境的配置及使用

CodeBlocks C++开发环境的配置及使用

CodeBlocks C开发环境的配置及使用 本文引用自作者编写的下述图书; 本文允许以个人学习、教学等目的引用、讲授或转载&#xff0c;但需要注明原作者"海洋饼干叔 叔"&#xff1b;本文不允许以纸质及电子出版为目的进行抄摘或改编。 1.《Python编程基础及应用》&#x…
阅读更多...
前端开发性能优化方案-14条

前端开发性能优化方案-14条

1、减少http请求数量。 单独得一个图片&#xff0c;js,css都是一个请求&#xff0c;将同类合并可以有效得减少请求个数。 2、使用CDN(内容分发网络) 需要新增服务器减少请求得站点个数&#xff08;靠钱解决需要买服务器&#xff09;。 3、添加Expire/Cache-Control头 Expi…
阅读更多...
GitHub标星百万的程序员转架构之路，竟被阿里用作内部晋升参考

GitHub标星百万的程序员转架构之路，竟被阿里用作内部晋升参考

架构师是很多程序员的奋斗目标&#xff0c;也可以说是职场生涯的一个重要选择方向&#xff0c;今天我就跟大家聊一聊如何从一个程序员成长为一个架构师。 首先我们先来看看架构师的定义到底是什么&#xff1f; 系统架构师是一个不仅需要主持整体又得需体察局部瓶颈并且依据详…
阅读更多...
Vulkan API的性能及兼容性

Vulkan API的性能及兼容性

1&#xff09;Vulkan API的性能及兼容性 ​2&#xff09;FrameTiming.gpuFrameTime获取GPU耗时有什么条件 3&#xff09;MMO里面的寻路网格如何制作 4&#xff09;万国这种联盟边界的实现思路 这是第314篇UWA技术知识分享的推送。今天我们继续为大家精选了若干和开发、优化相关…
阅读更多...
（九）笔记.net学习之委托和事件、多播委托、观察者模式

（九）笔记.net学习之委托和事件、多播委托、观察者模式

1.委托得声明、实例化和调用 &#xff08;1&#xff09;委托&#xff1a;本质是一个类&#xff0c;继承自System.MulticastDelegate,里面内置了几个方法&#xff0c;如构造函数等。 &#xff08;2&#xff09;声明委托&#xff1a;委托无方法体&#xff0c;可以有返回值或参数…
阅读更多...
Linux文件系统和软硬连接

Linux文件系统和软硬连接

目录 1.文件组成 2.文件系统 3.软硬连接 1.文件组成 先来看看文件的属性部分&#xff1a; 文件属性由权限&#xff0c;硬连接数量&#xff0c;所属组&#xff0c;所属人&#xff0c;大小和修改时间构成。 再来看看文件由的一个的东西inode 793395 793328就是inode 2.文件系…
阅读更多...
聚观早报 |中国企业成世界杯最大金主；马斯克恐失去世界首富位置

聚观早报 |中国企业成世界杯最大金主；马斯克恐失去世界首富位置

今日要闻&#xff1a;中国企业成世界杯最大金主&#xff1b;马斯克恐失去世界首富位置&#xff1b;刘强东称对不起京东高管&#xff1b;苹果在沪最大代工厂重启招工&#xff1b;威马汽车上海全员工资打折中国企业成世界杯最大金主 据报道&#xff0c;作为全球最为瞩目的赛事之一…
阅读更多...
谁懂，java后端面试多次惨败并发的苦！幸好有阿里首发并发编程学习文档，系统全面还便于上手！

谁懂，java后端面试多次惨败并发的苦！幸好有阿里首发并发编程学习文档，系统全面还便于上手！

什么是并发 并发指的在操作系统中&#xff0c;是指一个时间段中有几个程序都处于已启动运行到运行完毕之间&#xff0c;且这几个程序都是在同一个处理机上运行&#xff0c;但任一个时刻点上只有一个程序在处理机上运行。 并发和并行是十分容易混淆的概念。并发指的是多个任务交…
阅读更多...
如何测试 esp-matter_example_light 例程

如何测试 esp-matter_example_light 例程

此例程支持三种配网方式&#xff1a; 苹果手机扫码配网chip-tool 命令配网Matter 指令配网 1 使用苹果手机扫码配网 说明文档&#xff1a;Apple Matter 测试方法 所需设备&#xff1a; 苹果手机&#xff08;最新版本 IOS 系统&#xff09;苹果音响&#xff08;Apple-Matter&a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023