参考资料

• https://github.com/udacity/CarND-MPC-Quizzes/blob/master/install_Ipopt_CppAD.md

• https://blog.csdn.net/qq_34525916/article/details/119186692#:~:text=%E6%A6%82%E8%A7%88

• https://coin-or.github.io/CppAD/doc/install.htm

• Ubuntu20.04 安装 Ipopt + cppAD流程

• coinor库的安装与问题解决

• Undefined reference to `Ipopt::IpoptApplication::IpoptApplication(bool, bool)’

在进行cppad和ipopt的安装时，发现在按照其他博主写的博客进行安装时总是会出现各种各样他们没遇到的问题，所以这里也记录下自己成功安装的步骤。

1. Ipopt安装

这边提供3种方式进行安装，可以先尝试使用方式1，方式1不行的话尝试方式2，方式2不行最后再尝试方式3.

1. 方式1： 命令行安装

sudo apt-get install coinor-libipopt

我这边使用命令行安装时显示无法定位软件包，在更新软件源后依旧无法生效，所以这个方式我放弃了。

2. 方式2：源码安装

1. 安装依赖

   sudo apt-get install gcc g++ gfortran git patch wget pkg-config liblapack-dev libmetis-dev libblas-dev 
   

2. 创建一个存放所有跟Ipopt相关的文件夹，便于管理

   mkdir ~/Ipopt_pkg
   cd Ipopt_pkg
   

3. 安装ASL

   git clone https://github.com/coin-or-tools/ThirdParty-ASL.git
   cd ThirdParty-ASL
   sudo ./get.ASL
   sudo ./configure
   sudo make
   sudo make install
   cd ..
   

4. 安装HSL

   git clone https://github.com/coin-or-tools/ThirdParty-HSL.git
   cd ThirdParty-HSL
   # 接下来需要下载coinhsl文件，并解压到ThirdParty-HSL目录下
   

   下载coinhsl文件，并解压到ThirdParty-HSL目录下

   在ThirdParty-HSL目录下，执行以下命令

   sudo ./configure
   sudo make
   sudo make install
   cd ..
   

5. 安装MUMPS

   git clone https://github.com/coin-or-tools/ThirdParty-Mumps.git
   cd ThirdParty-Mumps
   sudo ./get.Mumps
   sudo ./configure
   sudo make
   sudo make install
   cd ..
   

6. 安装Ipopt

   git clone https://github.com/coin-or/Ipopt.git
   cd Ipopt
   mkdir build
   cd build
   sudo ../configure
   sudo make
   sudo make test
   sudo make install
   

7. 完善环境

   cd /usr/local/include
   sudo cp coin-or coin -r
   sudo ln -s /usr/local/lib/libcoinmumps.so.3 /usr/lib/libcoinmumps.so.3
   sudo ln -s /usr/local/lib/libcoinhsl.so.2 /usr/lib/libcoinhsl.so.2
   sudo ln -s /usr/local/lib/libipopt.so.3 /usr/lib/libipopt.so.3
   

到这里都没有报错则安装完成。

3. 方式3：源码安装

1. 首先，安装依赖

   sudo apt-get install gfortran
   apt-get install unzip
   

2. 下载Ipopt压缩包，并解压。

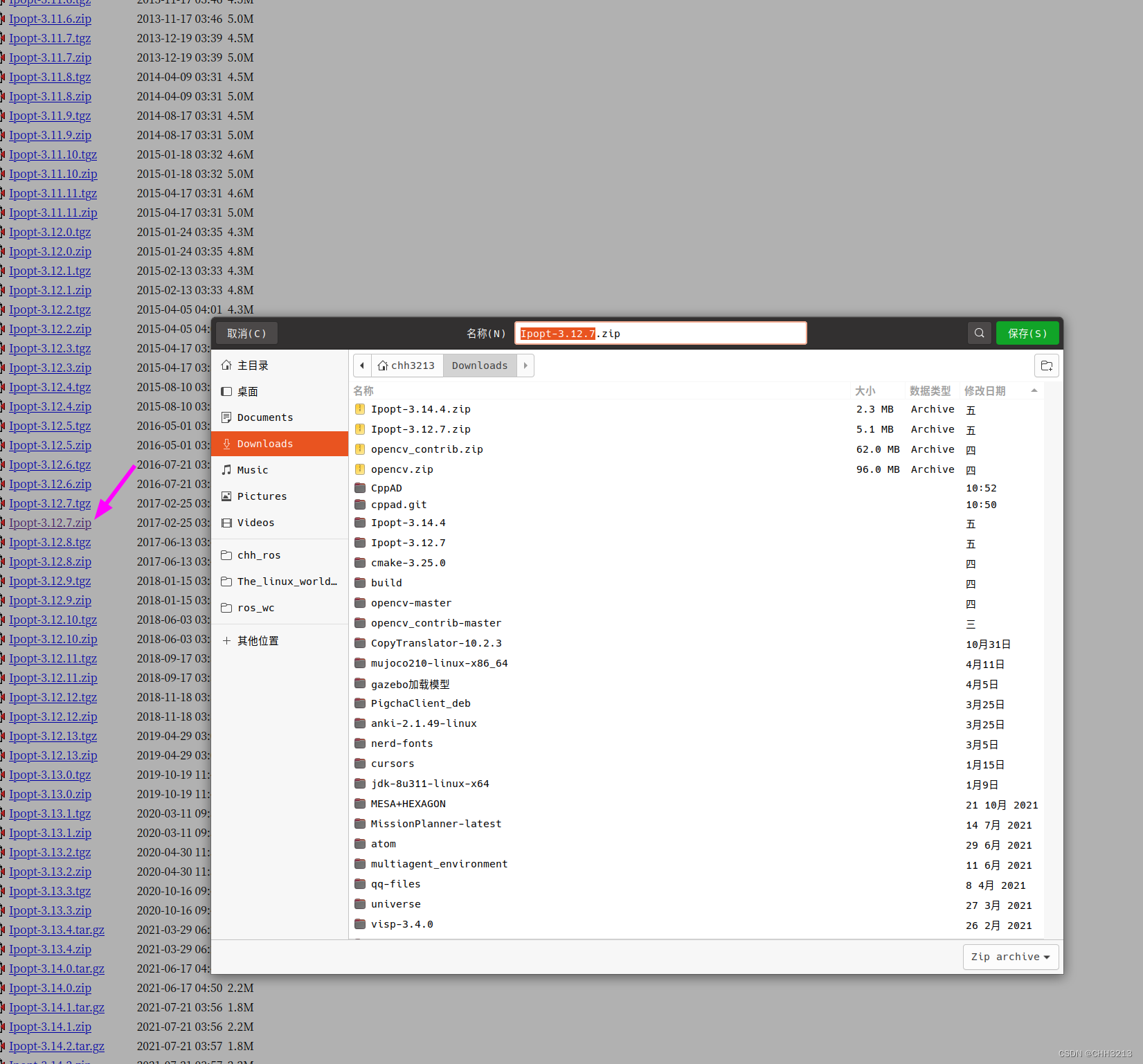
   wget https://www.coin-or.org/download/source/Ipopt/Ipopt-3.12.7.zip 
   unzip Ipopt-3.12.7.zip
   

   在使用wget方式下载Ipopt压缩包时，可能因为网络原因下载不了，那么可以直接进入网址，找到Ipopt-3.12.7.zip进行手动下载即可。
   

3. 下载并解压完成后，进入Ipopt-3.12.7文件夹，执行新建文件 install_ipopt.sh

   touch install_ipopt.sh
   

4. 打开该文件，并写入以下内容：

   # Pass the Ipopt source directory as the first argument
   if [ -z $1 ]
   then
       echo "Specifiy the location of the Ipopt source directory in the first argument."
       exit
   fi
   cd $1
   
   prefix=/usr/local
   srcdir=$PWD
   
   echo "Building Ipopt from ${srcdir}"
   echo "Saving headers and libraries to ${prefix}"
   
   # BLAS
   cd $srcdir/ThirdParty/Blas
   ./get.Blas
   mkdir -p build && cd build
   ../configure --prefix=$prefix --disable-shared --with-pic
   make install
   
   # Lapack
   cd $srcdir/ThirdParty/Lapack
   ./get.Lapack
   mkdir -p build && cd build
   ../configure --prefix=$prefix --disable-shared --with-pic \
       --with-blas="$prefix/lib/libcoinblas.a -lgfortran"
   make install
   
   # ASL
   cd $srcdir/ThirdParty/ASL
   ./get.ASL
   
   # MUMPS
   cd $srcdir/ThirdParty/Mumps
   ./get.Mumps
   
   # build everything
   cd $srcdir
   ./configure --prefix=$prefix coin_skip_warn_cxxflags=yes \
       --with-blas="$prefix/lib/libcoinblas.a -lgfortran" \
       --with-lapack=$prefix/lib/libcoinlapack.a
   make
   make test
   make -j1 install
   

5. 给该文件添加可执行权限：

   sudo chmod +x install_ipopt.sh
   

6. 然后运行脚本：

   ./install_ipopt.sh Ipopt-3.12.7
   

   运行脚本后，有可能因为网络问题运行失败，可以多尝试几次。
   

最后静静等待安装即可。

最终，我是使用方式2步骤进行安装的。方式3因为网络问题，比较难成功。

4. Ipopt测试

进入 IPOPT 源码文件夹如下位置，用官方例子测试

cd Ipopt/build/examples/Cpp_example
sudo make
./Cpp_example

出现以下界面说明安装成功

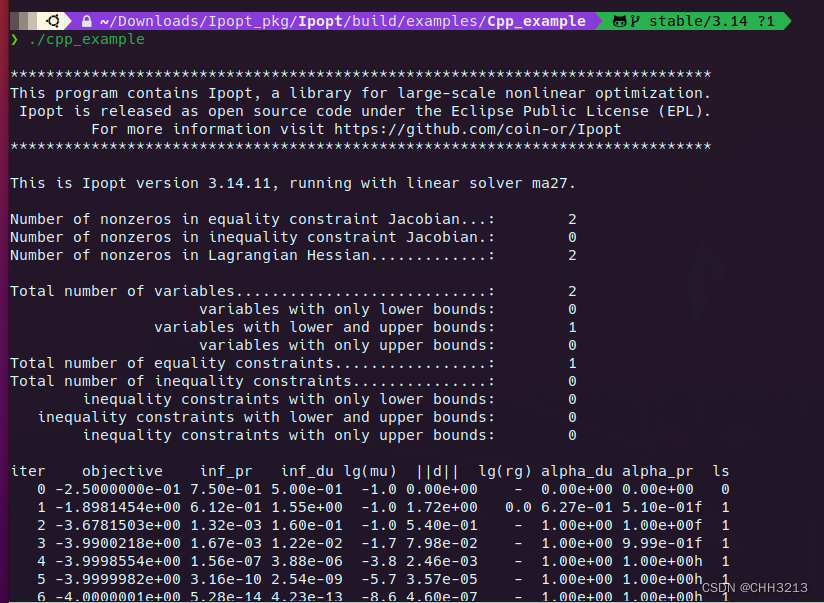
5. 报错修复

安装完成后，有可能后期在使用阶段会编译报错：

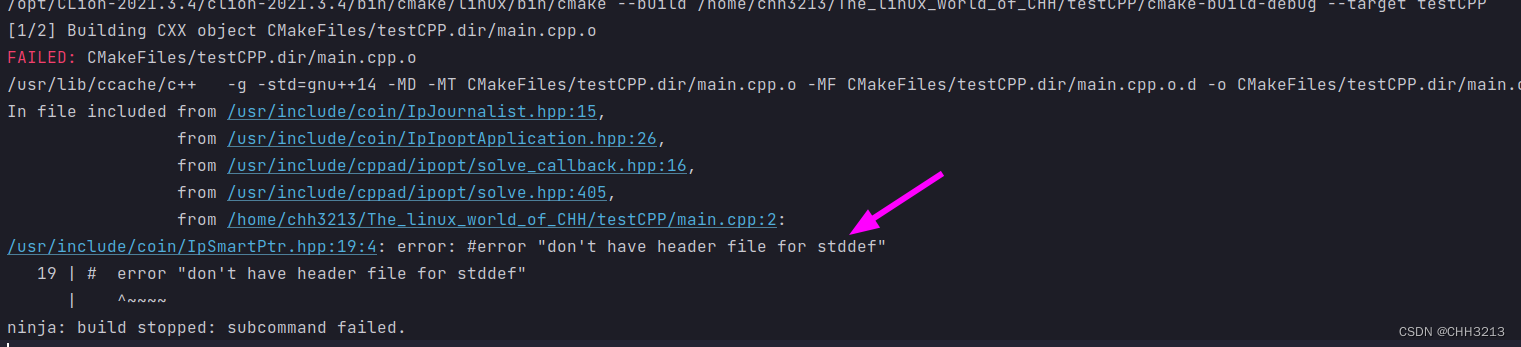
/usr/include/coin/IpSmartPtr.hpp:19:4: error: #error "don't have header file for stddef"

需要通过以下方式解决。

打开文件

sudo gedit /usr/include/coin/IpSmartPtr.hpp

在文件的预处理部分，添加如下内容

#define HAVE_CSTDDEF // 添加部分
#ifdef HAVE_CSTDDEF
# include <cstddef>
#else
# ifdef HAVE_STDDEF_H
#  include <stddef.h>
# else
#  error "don't have header file for stddef"
# endif
#endif
#undef HAVE_CSTDDEF // 添加部分

2. CppAD安装

先尝试方式1，方式1不行再尝试方式2。

1. 方式1：命令行安装

一般网上已有的教程都是说直接在终端中输入以下命令安装：

sudo apt-get install cppad

但是，使用这种方式可能找不到该库。

遇到这个问题时，可以尝试切换源。切换源方式见博客。切换源后再进行更新。

sudo apt update

然后再重新尝试安装。

安装完成后如果需要卸载，则执行以下命令：

sudo apt-get remove cppad

如果上述方式无法成功安装，可采取下面源码的方式安装。

2. 方式2：源码方式安装

使用源码的方式安装。

1. 下载源码：

   git clone https://github.com/coin-or/CppAD.git 
   

2. 下载完成后，进入CppAD文件夹，然后执行以下命令：

   mkdir build
   cd build
   cmake ..
   make 
   sudo make install
   

   即可安装成功。

3. 如果需要卸载的话，在CppAD/build文件夹内执行以下命令即可：

   	sudo make uninstall
   

3. CppAD测试

使用以下代码测试CppAD是否安装成功。

• CppAD_demo.cpp文件

  # include <iostream>        // standard input/output
  # include <vector>          // standard vector
  # include <cppad/cppad.hpp> // the CppAD package
  
  namespace { // begin the empty namespace
      // define the function Poly(a, x) = a[0] + a[1]*x[1] + ... + a[k-1]*x[k-1]
      template <class Type>
      Type Poly(const CPPAD_TESTVECTOR(double) &a, const Type &x)
      {   size_t k  = a.size();
          Type y   = 0.;  // initialize summation
          Type x_i = 1.;  // initialize x^i
          for(size_t i = 0; i < k; i++)
          {   y   += a[i] * x_i;  // y   = y + a_i * x^i
              x_i *= x;           // x_i = x_i * x
          }
          return y;
      }
  }
  // main program
  int main(void)
  {   using CppAD::AD;   // use AD as abbreviation for CppAD::AD
      using std::vector; // use vector as abbreviation for std::vector
  
      // vector of polynomial coefficients
      size_t k = 5;                  // number of polynomial coefficients
      CPPAD_TESTVECTOR(double) a(k); // vector of polynomial coefficients
      for(size_t i = 0; i < k; i++)
          a[i] = 1.;                 // value of polynomial coefficients
  
      // domain space vector
      size_t n = 1;               // number of domain space variables
      vector< AD<double> > ax(n); // vector of domain space variables
      ax[0] = 3.;                 // value at which function is recorded
  
      // declare independent variables and start recording operation sequence
      CppAD::Independent(ax);
  
      // range space vector
      size_t m = 1;               // number of ranges space variables
      vector< AD<double> > ay(m); // vector of ranges space variables
      ay[0] = Poly(a, ax[0]);     // record operations that compute ay[0]
  
      // store operation sequence in f: X -> Y and stop recording
      CppAD::ADFun<double> f(ax, ay);
  
      // compute derivative using operation sequence stored in f
      vector<double> jac(m * n); // Jacobian of f (m by n matrix)
      vector<double> x(n);       // domain space vector
      x[0] = 3.;                 // argument value for computing derivative
      jac  = f.Jacobian(x);      // Jacobian for operation sequence
  
      // print the results
      std::cout << "f'(3) computed by CppAD = " << jac[0] << std::endl;
  
      // check if the derivative is correct
      int error_code;
      if( jac[0] == 142. )
          error_code = 0;      // return code for correct case
      else  error_code = 1;    // return code for incorrect case
  
      return error_code;
  }
  

• CMakeLists.txt文件

  cmake_minimum_required(VERSION 3.21)
  
  project(testCPP)
  
  set(CMAKE_CXX_STANDARD 14)
  
  add_executable(CppAD_demo CppAD_demo.cpp)
  
  

• 在该项目目录内执行

  mkdir build
  cd build
  cmake ../
  make
  ./CppAD_demo
  

  输出以下信息，则CppAD安装成功
  

3. 测试Ipopt与CppAD是否可用

以下例子来自于博客。

1. 例子

利用CppAD与Ipopt求解以下非线性规划问题

$$\begin{array}{cc}\mathrm{minimize}& x_1{x}_4\left(x_1+x_2+x_3\right)+x_3\\ \text{ s.t. }& x_1{x}_2{x}_3{x}_4\ge 25\\ & x_1^2+x_2^2+x_3^2+x_4^2=40\\ & 1\le x_1,x_2,x_3,x_4\le 5\end{array}$$

• cppad_ipopt_demo.cpp文件

  #include <iostream>
  #include <cppad/ipopt/solve.hpp>
  
  using namespace std;
  
  namespace {
  using CppAD::AD;
  class FG_eval {
  public:
      typedef CPPAD_TESTVECTOR(AD<double>) ADvector;
      void operator()(ADvector& fg, const ADvector& x)
      {
          assert(fg.size() == 3);
          assert(x.size() == 4);
          // variables
          AD<double> x1 = x[0];
          AD<double> x2 = x[1];
          AD<double> x3 = x[2];
          AD<double> x4 = x[3];
          // f(x) objective function
          fg[0] = x1 * x4 * (x1 + x2 + x3) + x3;
          // constraints
          fg[1] = x1 * x2 * x3 * x4;
          fg[2] = x1 * x1 + x2 * x2 + x3 * x3 + x4 * x4;
          return;
      }
  
  };
  
  }
  
  bool get_started(void)
  {
      bool ok = true;
      size_t i;
      typedef CPPAD_TESTVECTOR(double) Dvector;
  
      size_t nx = 4; // number of varibles
      size_t ng = 2; // number of constraints
      Dvector x0(nx); // initial condition of varibles
      x0[0] = 1.0;
      x0[1] = 5.0;
      x0[2] = 5.0;
      x0[3] = 1.0;
  
      // lower and upper bounds for varibles
      Dvector xl(nx), xu(nx);
      for(i = 0; i < nx; i++)
      {
          xl[i] = 1.0;
          xu[i] = 5.0;
      }
      Dvector gl(ng), gu(ng);
      gl[0] = 25.0;    gu[0] = 1.0e19;
      gl[1] = 40.0;    gu[1] = 40.0;
      // object that computes objective and constraints
      FG_eval fg_eval;
  
      // options
      string options;
      // turn off any printing
      options += "Integer print_level  0\n";
      options += "String sb            yes\n";
      // maximum iterations
      options += "Integer max_iter     10\n";
      //approximate accuracy in first order necessary conditions;
      // see Mathematical Programming, Volume 106, Number 1,
      // Pages 25-57, Equation (6)
      options += "Numeric tol          1e-6\n";
      //derivative tesing
      options += "String derivative_test   second-order\n";
      // maximum amount of random pertubation; e.g.,
      // when evaluation finite diff
      options += "Numeric point_perturbation_radius   0.\n";
  
  
      CppAD::ipopt::solve_result<Dvector> solution; // solution
      CppAD::ipopt::solve<Dvector, FG_eval>(options, x0, xl, xu, gl, gu, fg_eval, solution); // solve the problem
  
      cout<<"solution: "<<solution.x<<endl;
  
      //
      //check some of the solution values
      //
      ok &= solution.status == CppAD::ipopt::solve_result<Dvector>::success;
      //
      double check_x[]  = {1.000000, 4.743000, 3.82115, 1.379408};
      double check_zl[] = {1.087871, 0.,       0.,       0.      };
      double check_zu[] = {0.,       0.,       0.,       0.      };
      double rel_tol    = 1e-6; // relative tolerance
      double abs_tol    = 1e-6; // absolute tolerance
      for(i = 0; i < nx; i++)
      {
          ok &= CppAD::NearEqual(
                      check_x[i], solution.x[i], rel_tol, abs_tol);
          ok &= CppAD::NearEqual(
                      check_zl[i], solution.zl[i], rel_tol, abs_tol);
          ok &= CppAD::NearEqual(
                      check_zu[i], solution.zu[i], rel_tol, abs_tol);
      }
  
      return ok;
  }
  
  int main()
  {
      cout << "CppAD : Hello World Demo!" << endl;
      get_started();
      return 0;
  }
  

• CMakeLists.txt文件

  cmake_minimum_required(VERSION 3.21)
  project(testCPP)
  
  set(CMAKE_CXX_STANDARD 14)
  
  add_executable(cppad_ipopt_demo cppad_ipopt_demo.cpp)
  target_link_libraries(cppad_ipopt_demo ipopt)
  

• 在该项目目录内执行

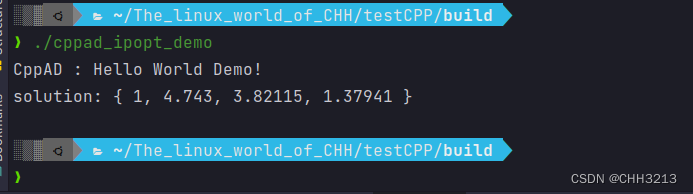
  mkdir build
  cd build
  cmake ../
  make
  ./cppad_ipopt_demo
  

  若输出如下信息，则说明Ipopt与CppAD安装成功。

  

2. 编译报错解决

1. Undefined reference to `Ipopt::IpoptApplication::IpoptApplication(bool, bool)’

这里需要注意的是，CMakeLists.txt文件需要加入target_link_libraries(cppad_ipopt_demo ipopt)链接，否则会报如下错误：

Undefined reference to `Ipopt::IpoptApplication::IpoptApplication(bool, bool)'

2. fatal error: coin/IpIpoptApplication.hpp: No such file or directorycompilation terminated.

若编译后报错：

fatal error: coin/IpIpoptApplication.hpp: No such file or directorycompilation terminated.

这是由缺少coin_or库引起的，可以执行以下命令安装

sudo apt install coinor-libipopt-dev

以上所有代码存于github仓库。