目录

一.每天学一个知识点

1.涉及公式

1.s.trim()

2.substring() 可以看出是满足一系列合法条件的时候,就会返回一个新的字符串.

1.思路1 栈

思路2:stringbulider

二,二叉树相关OJ题

1.检查两颗树是否相同

2.另一颗树的子树。

3.判断一颗二叉树是否是平衡二叉树

1.时间复杂度o(n^2)方法

2.时间复杂度为O(n)的做法

4.遍历二叉树建立

5.对称二叉树的判断

---

 

一.每天学一个知识点

1.涉及公式

1.s.trim()

第一个循环找到开头的st下标.第二个循环找到结尾的.

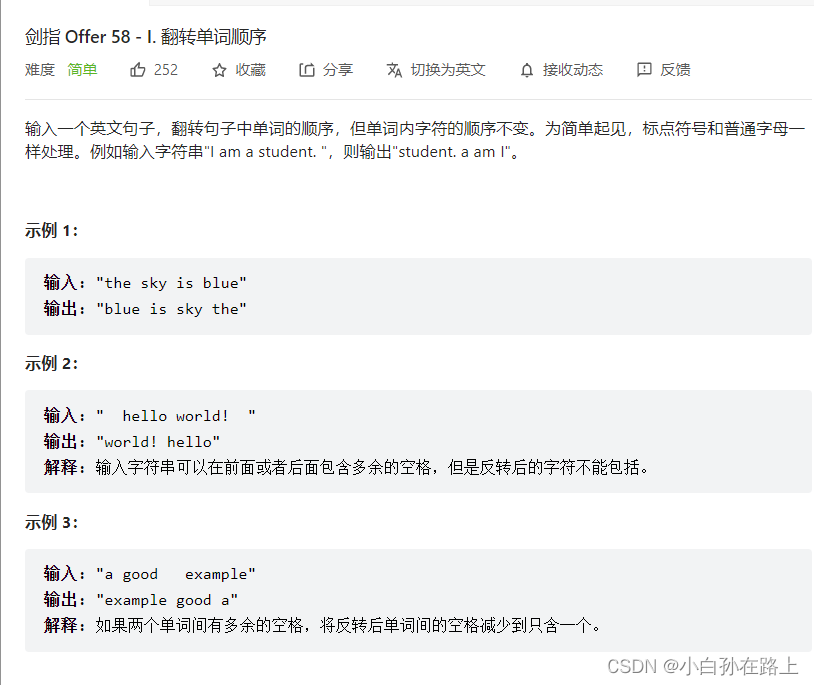
2.substring() 可以看出是满足一系列合法条件的时候,就会返回一个新的字符串.

这里注意,from就是左臂右开的

s.substring s = s.trim() math.abs

1.思路1 栈

把元素从后往前压入栈中,如果遇到空格,就用sb接收弹出来的值,

如果遇到第一个元素且不是空格还要再次判断一次.

思路2:stringbulider

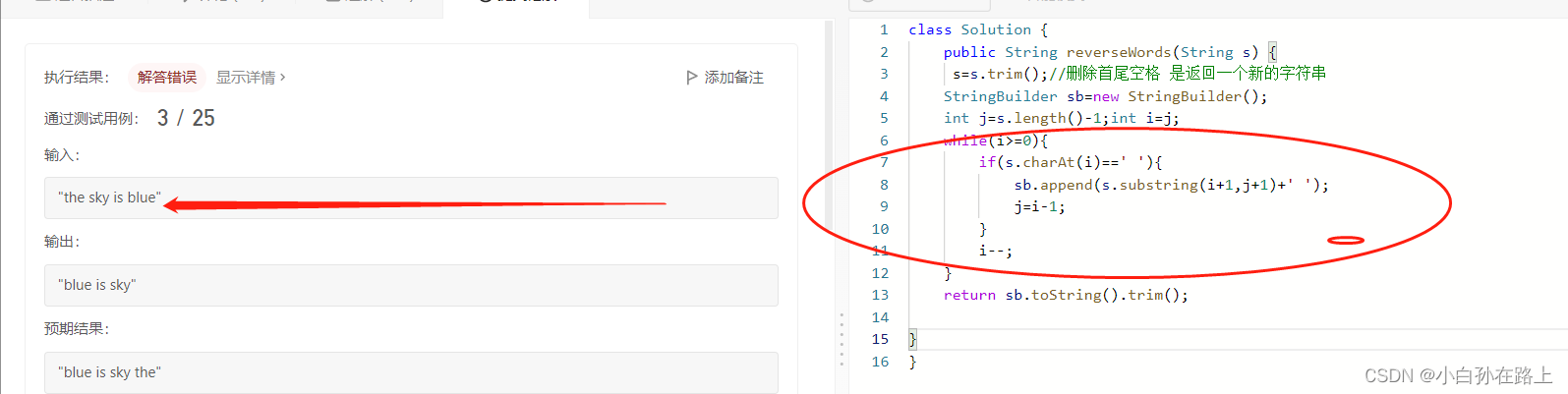
没有考虑最后一个单词的情况就算考虑到了,也不能处理两个单词间有空格的情况

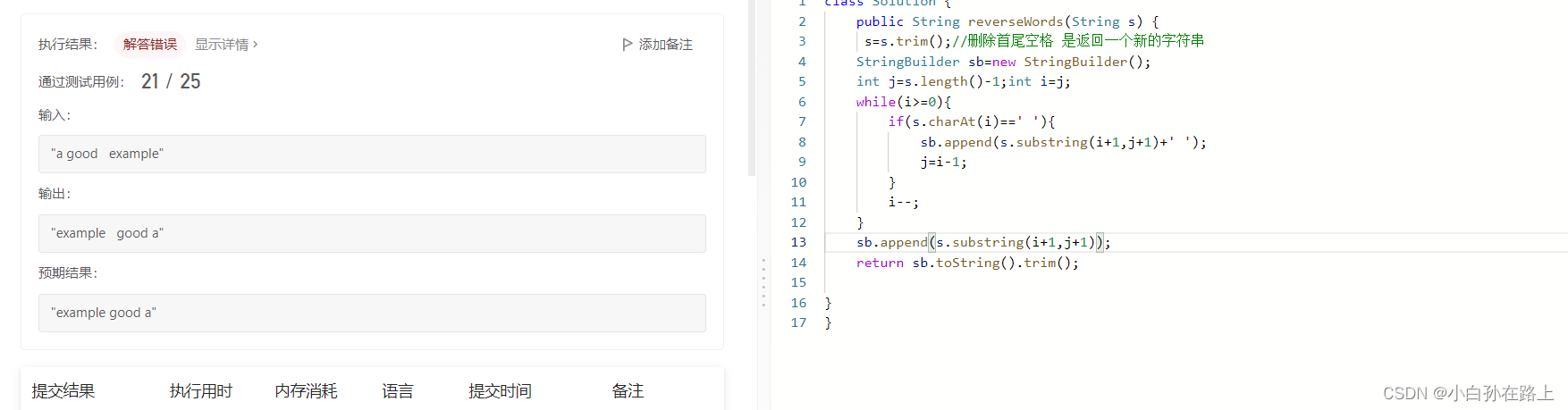
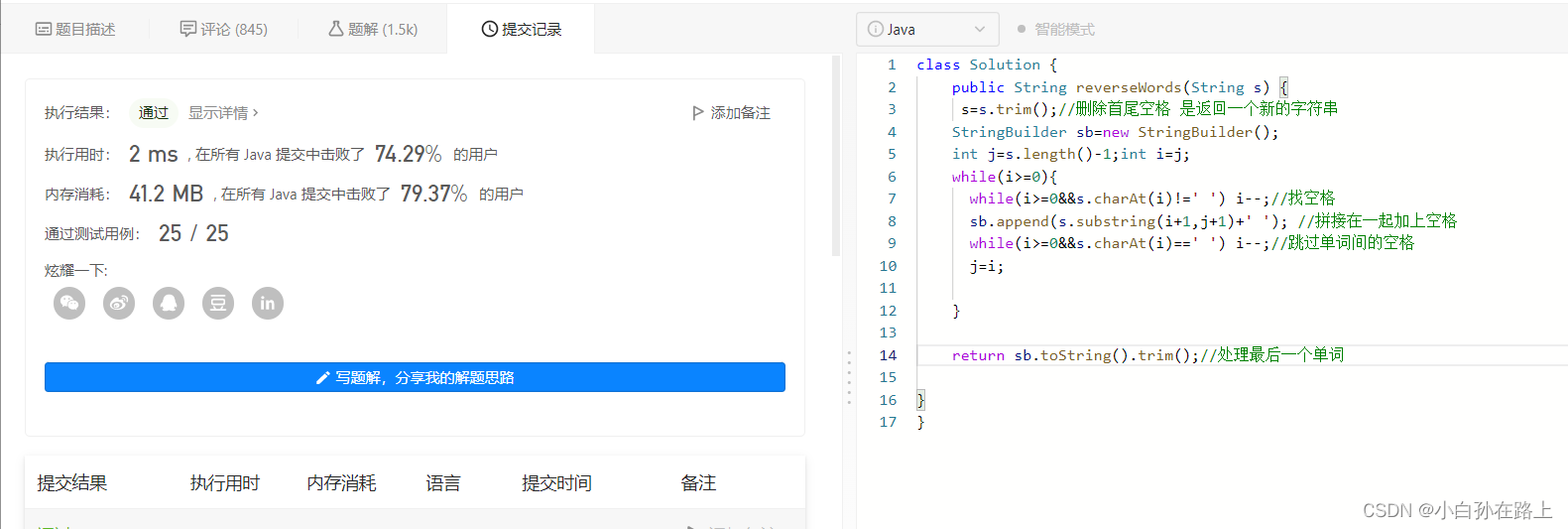
class Solution {
    public String reverseWords(String s) {
     s=s.trim();//删除首尾空格 是返回一个新的字符串
    StringBuilder sb=new StringBuilder();
    int j=s.length()-1;int i=j;
    while(i>=0){
      while(i>=0&&s.charAt(i)!=' ') i--;//找空格
      sb.append(s.substring(i+1,j+1)+' '); //拼接在一起加上空格
      while(i>=0&&s.charAt(i)==' ') i--;//跳过单词间的空格
      j=i;

    }
   
    return sb.toString().trim();//处理最后一个单词

}
}

二,二叉树相关OJ题

1.检查两颗树是否相同

思路:不仅树节点结构相同也就是不能有一个为null有一个不为null.而且要求两个值要相同

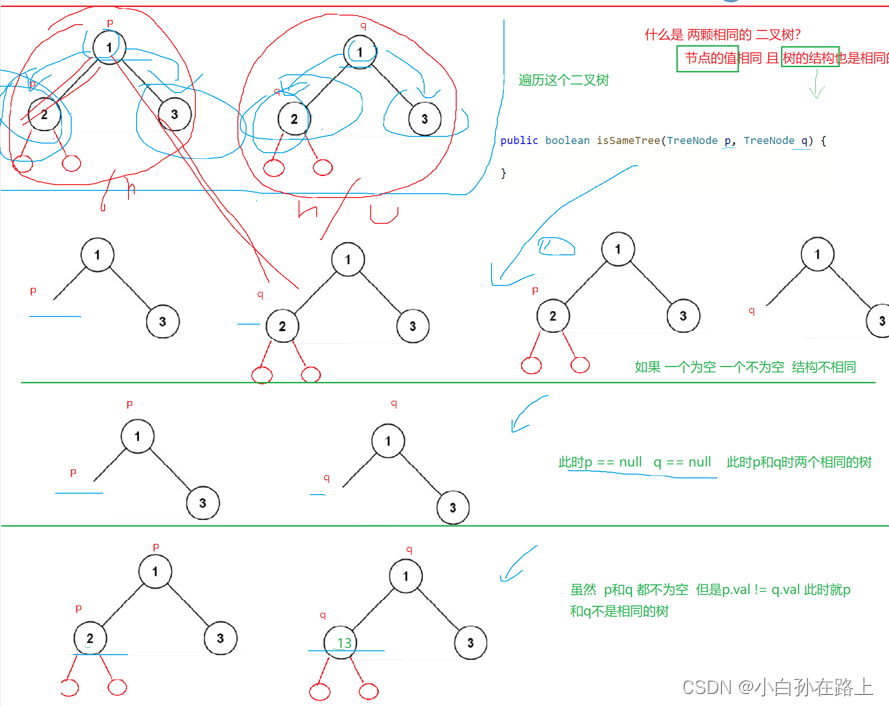
 public boolean isSameTree(TreeNode p, TreeNode q) {
       if(p == null && q !=null ||p!=null&&q==null) return false;
       if(p==null&&q==null)return true;
       if(p.val==q.val) return true;
       //如果这样的话,假设两个相同,就没办法往下走了,就永远递归不了,直接返回true
       //必须要求都满足条件,再往下递归
       return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);
    }

此方法耦合度高且可读性差

class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if(p!=null&&q!=null){
            if(p.val!=q.val){
                return false;
            }
        }else if(p==null&&q==null){
            return true;

        }else{
            return false;
        }
       boolean b= isSameTree(p.left,q.left);
       if(b){
        b=isSameTree(p.right,q.right);
       }
       return b;


    }
}

2.另一颗树的子树。

思路:要么就判断是否是相同的树,或者是他的左子树或者右子树是否相同,然后继续递归.

class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q){
        if(p==null&&q!=null||p!=null&&q==null) return false;
        if(p==null&&q==null) return true;
        if(p.val!=q.val) return false;
        return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);
    }
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if(root==null) return false;
        if(isSameTree(root,subRoot)) return true;
        return isSubtree(root.left,subRoot)||isSubtree(root.right,subRoot);
    }
}

3.判断一颗二叉树是否是平衡二叉树

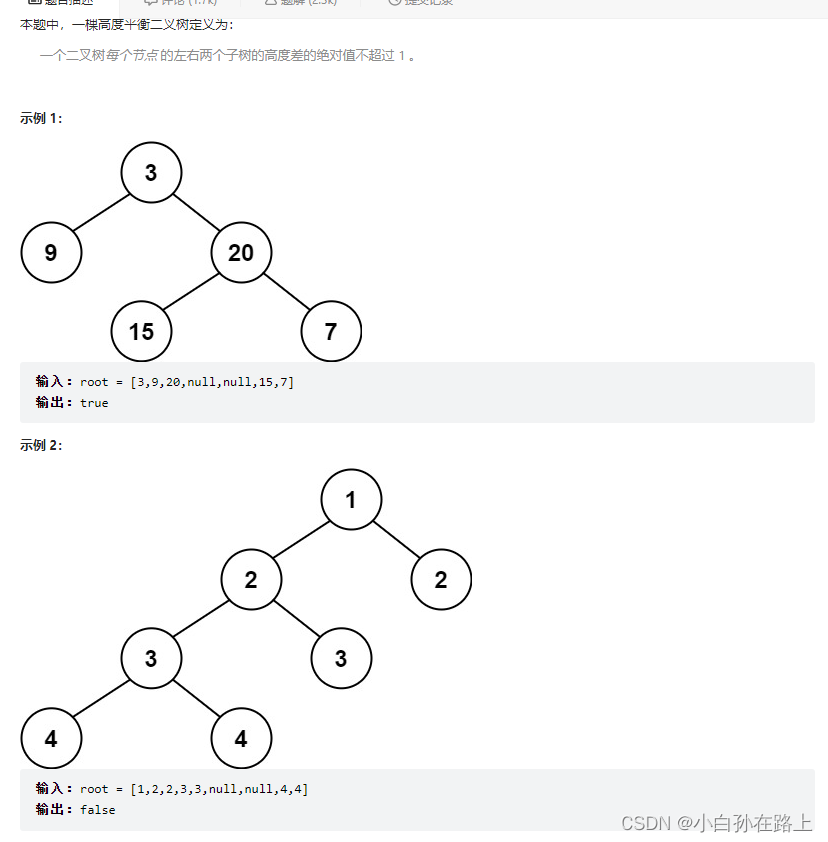
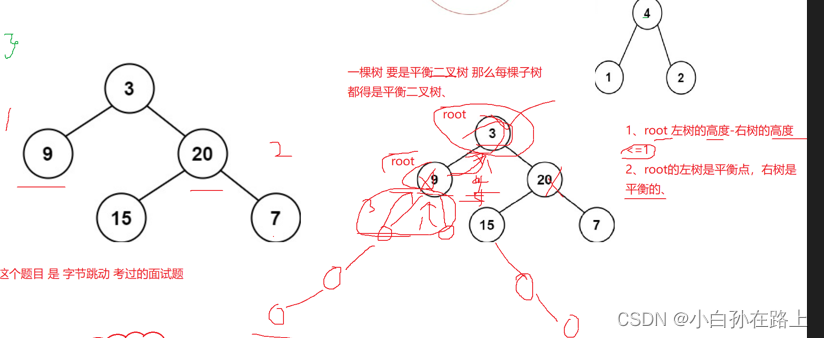
思路:如果是平衡二叉树那么每颗子树都是平衡二叉树,所以又要递归

1.时间复杂度o(n^2)方法

class Solution {
    public int treeHeight(TreeNode root){
        if(root==null) return 0;
        int heightLeft=treeHeight(root.left);
        int heightright=treeHeight(root.right);  
        return heightLeft>heightright?heightLeft+1:heightright+1;

    }
    public boolean isBalanced(TreeNode root) {
        if(root==null) return true;   
        int heightLeft=treeHeight(root.left);
        int heightright=treeHeight(root.right);
        if(heightLeft-heightright>1){
            return false;
        }
        if(heightright-heightLeft>1){
            return false;
        }//如果是true,总长度满足,剩下的分支就不会管了.就不会往下递归了
        //走到这一行要求左右差距不超过1
        return isBalanced(root.left)&&isBalanced(root.right);
    }
}

2.时间复杂度为O(n)的做法

因为在求树的高度的时候就已经把每个节点递归了

然后再平衡树的方法的时候又把每个节点再拿进去求所以复杂度就是n*n

class Solution {
    public int treeHeight(TreeNode root){
        if(root==null) return 0;
        int heightLeft=treeHeight(root.left);
        int heightright=treeHeight(root.right);
        if(heightLeft>=0&&heightright>=0&&Math.abs(heightLeft-heightright)<=1){
            return Math.max(heightLeft,heightright)+1;
        }else{
            return -1;
        }
       

    }
    public boolean isBalanced(TreeNode root) {
        if(root==null) return true;
        return treeHeight(root)>=0;
  

    }
}

4.遍历二叉树建立

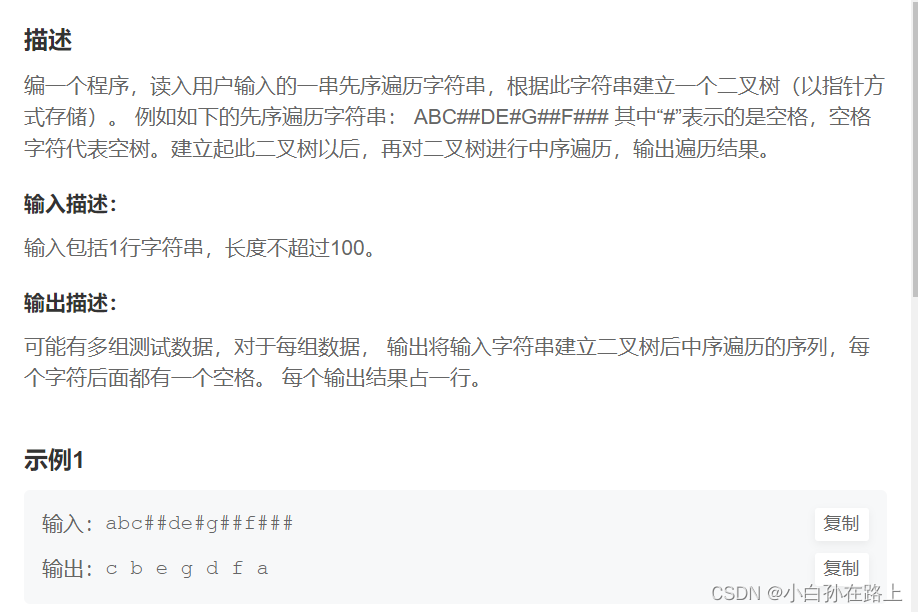
class TreeNode {
    TreeNode left;
    TreeNode right;
    char  val;
     TreeNode(char val) {
        this.val = val;
    }
}

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void inorder(TreeNode root){
        if(root==null) return;
        inorder(root.left);
        System.out.print(root.val+" ");
        inorder(root.right);

    }
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        // 注意 hasNext 和 hasNextLine 的区别
        while (in.hasNextLine()) { // 注意 while 处理多个 case
            String str = in.nextLine();
            TreeNode root = createTree(str);
            inorder(root);
            System.out.println();
            i=0;
        }

    }
    public static int i=0;
    public static TreeNode createTree(String str) {
        char ch=str.charAt(i);
        TreeNode root=null;
        if(ch!='#'){
            root=new TreeNode(ch);
            i++;
            root.left=createTree(str);
            root.right=createTree(str);
        }else{
            i++;
        }
        return root;
    }

}

5.对称二叉树的判断

也就是子树的左节点和另一棵树的右节点分别判断,也就是把判断两棵树是否相同改编一下就好

class Solution {
    public boolean issame(TreeNode p,TreeNode q){
        if(p!=null&&q==null) return false;
        if(p==null&&q!=null) return false;
        if(p==null&&q==null) return true;
        if(p.val!=q.val) return false;
        return issame(p.left,q.right)&&issame(p.right,q.left);

    }
    public boolean isSymmetric(TreeNode root) {
        if(root==null) return true;
        return issame(root.left,root.right);

    }
}