堆排序-算法实现

前面介绍了堆的基本功能实现(https://blog.csdn.net/m0_46343224/article/details/127986662)，了解了堆，这里用堆实现排序

1. 向上调整和向下调整比较

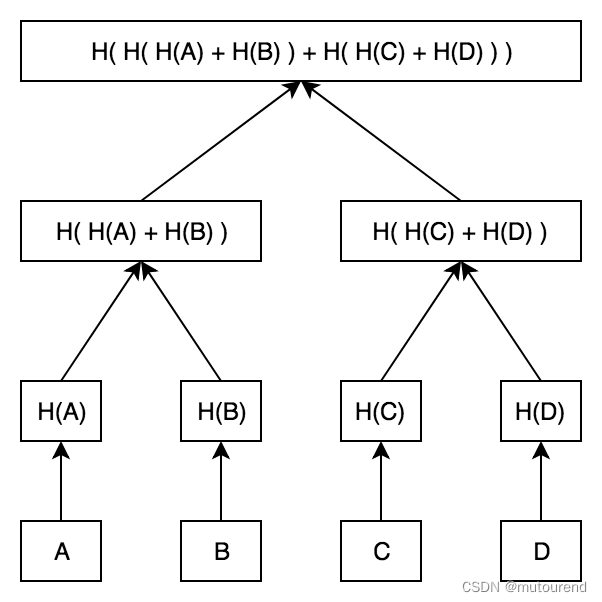
思考：向上调整和向下调整哪个更优？

此图解析：向上调整的时间复杂度：O(N*log₂(N));向下调整的时间复杂度：O(N)；则从尾向下调整优于向上调整

2. 堆排序

堆排序思路：

升序：首先建大堆，然后交换首尾数据（也就是把最大的数据放在尾部，再从头向下调整size-1个数据（也就是不对其交换后的最大的数据调整）

降序：首先建小堆，然后交换首尾数据（也就是把最大的数据放在尾部，再从头向下调整size-1个数据（也就是不对其交换后的最大的数据调整）

1. 升序

void SwapData(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

void AdjustDownSortAscending(int* a, int size, int parent)
{
	//假设默认左孩子大
	int lchild = parent * 2 + 1;

	while (lchild < size)
	{
		//确认指向大的孩子
		if (lchild + 1 < size && a[lchild + 1] > a[lchild])
		{
			++lchild;
		}
		//大堆
		//lchild + 1 < size 表示最后的父节点和左孩子对比
		if (a[parent] < a[lchild])
		{
			SwapData(&a[parent], &a[lchild]);
			parent = lchild;
			lchild = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapSortAscending(int* a, int size)
{
	//建大堆(从尾元素父节点开始)
	for (int i = (size - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDownSortAscending(a, size, i);
	}

	int heapend = size - 1;
	while (heapend > 0)
	{
		SwapData(&a[0], &a[heapend]);
        //从首开始向下调整
		AdjustDownSortAscending(a, heapend, 0);
		heapend--;
	}
}

2. 降序

void SwapData(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

void AdjustDownSortDescending(int* a, int size, int parent)
{
	//假设默认左孩子大
	int lchild = parent * 2 + 1;

	while (lchild < size)
	{
		//确认指向大的孩子
		if (lchild + 1 < size && a[lchild + 1] < a[lchild])
		{
			++lchild;
		}
		//大堆
		//lchild + 1 < size 表示最后的父节点和左孩子对比
		if (a[parent] > a[lchild])
		{
			SwapData(&a[parent], &a[lchild]);
			parent = lchild;
			lchild = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapSortDescending(int* a, int size)
{
	//建小堆(从尾元素父节点开始)
	for (int i = (size - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDownSortDescending(a, size,i);
	}

	int heapend = size - 1;
	while (heapend > 0)
	{
		SwapData(&a[0], &a[heapend]);
        //从首开始向下调整
		AdjustDownSortDescending(a, heapend, 0);
		heapend--;
	}
}