评价

它可以减少运行的时间，很多问题如果暴力求解需要O(n^2)的复杂度，而通过分治可以减少到O（nlogn）
当与随机化技术相结合时，分治的功能很强大

分治算法的步骤

1.先将大的问题分解为一个个小的子问题
2.对每一个子问题通过递归对他们进行求解
3.然后将求解后的子问题进行合并，就完成了对大问题的求解

经典问题

问题一：归并排序问题

Sort problem
INPUT: An array of n integers, denoted as A[0..n − 1]
OUTPUT: The elements of A in increasing order

想法一

将一个数组分为两部分，每次都去除最后一个元素，然后对前面剩余的元素进行排序。

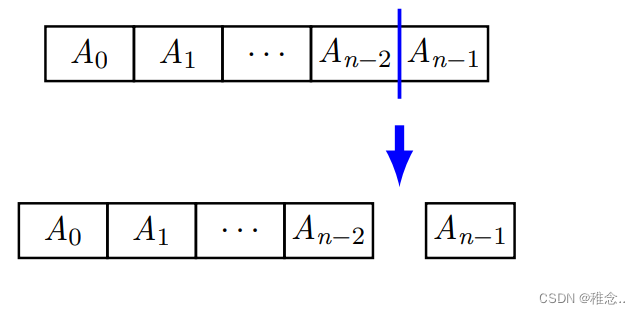
伪代码：

1: if k ≤ 1 then
2: return ;
3: end if
4: InsertionSort(A, k − 1);//排序前k-1个，要执行n次
5: key = A[k];
6: i = k − 1;
7: while i ≥ 0 and A[i] > key do//将第k个插入，插入时间为O(n)
8: A[i + 1] = A[i];
9: i − −;
10: end while
11: A[i + 1] = key;

这种分治的方法也可以解决问题，但他的时间复杂度为O(n^2)，并没有节约时间。
证明：T(n) = T(n − 1) + O(n) = O(n^2).

想法二

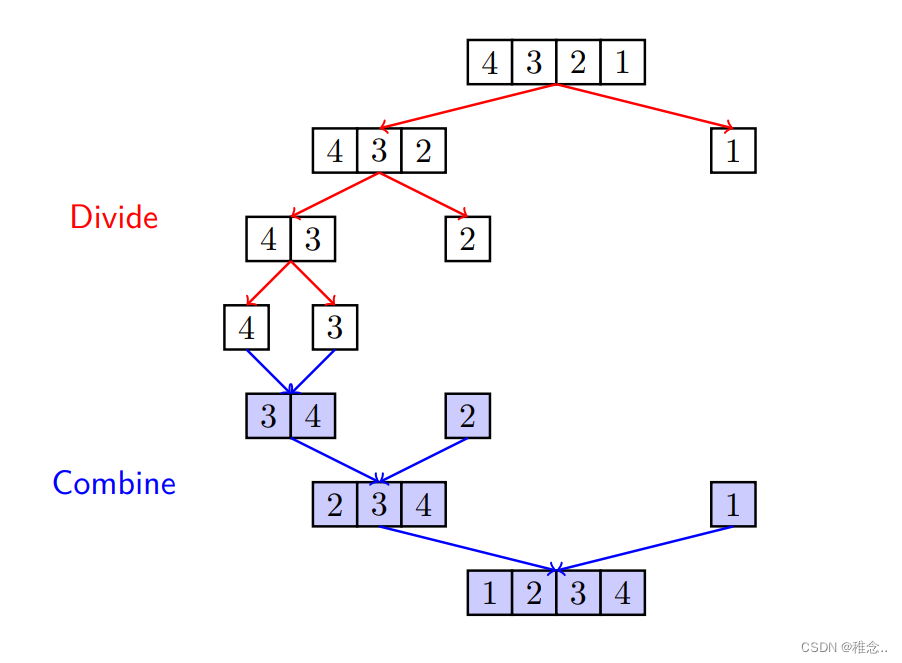
从中间分，将一个数组一分为二成两个差不多大的数组。

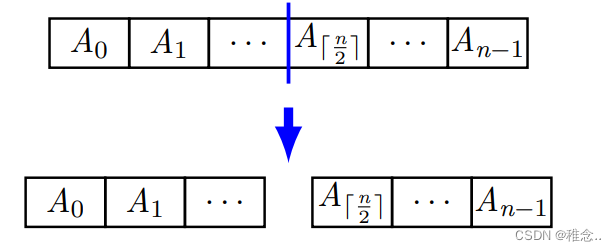
1: //Sort elements in A[l..r]
2: if l < r then
3: m = (l + r)/2; //m denotes the middle point
4: MergeSort(A, l, m );
5: MergeSort(A, m + 1, r);
6: Merge(A, l, m, r); //Combining the sorted arrays
7: end if

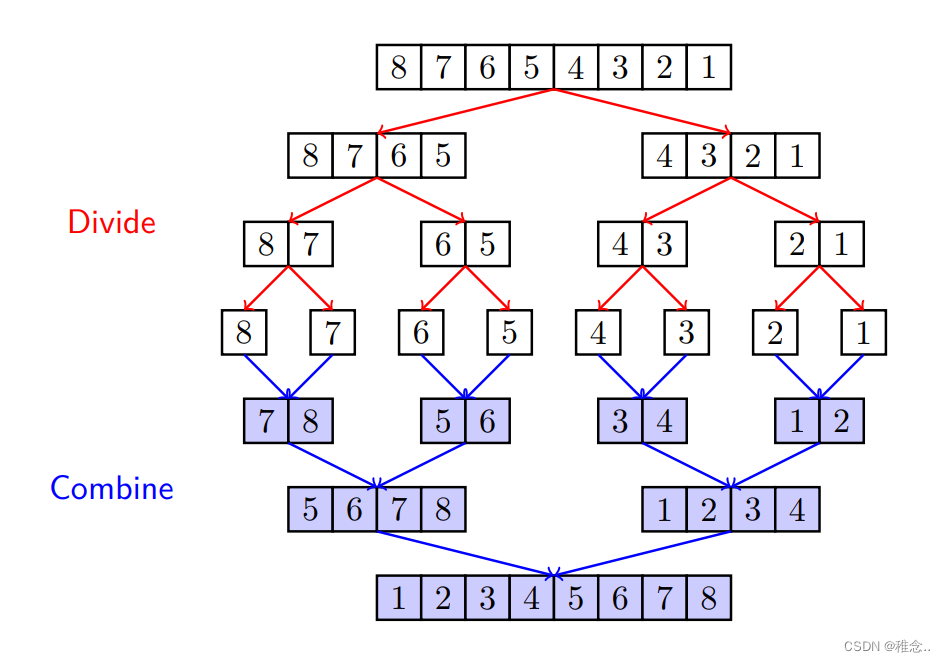
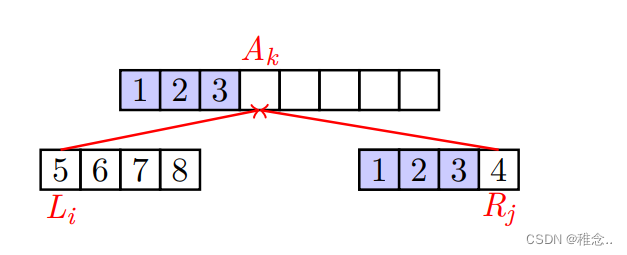
合并算法的实现为:

Merge (A, l, m, r)
1: //Merge A[l..m] (denoted as L) and A[m + 1..r] (denoted as R).
2: i = 0; j = 0;
3: for k = l to r do
4: if L[i] < R[j] then
5: A[k] = L[i];
6: i + +;
7: if all elements in L have been copied then
8: Copy the remainder elements from R into A;
9: break;
10: end if
11: else
12: A[k] = R[j];
13: j + +;
14: if all elements in R have been copied then
15: Copy the remainder elements from L into A;
16: break;
17: end if
18: end if
19: end for

此时它的时间复杂度为：O(nlogn),比想法一的要快很多，由此可以看出，这种划分的策略是更好的

问题二:逆序对问题

CountingInversion problem
INPUT: An array A[0..n − 1] with n distinct numbers;
OUTPUT: the number of inversions. A pair of indices i and j
constitutes an inversion if i < j but A[i] > A[j].

这个问题可以用暴力的办法来求解，但是需要花费的时间为O(n^2)，我们可以考虑用分治的思想来进行求解。
首先将原先的数组一分为二，然后对分开的每一部分求出它的逆序对数，最后在合并的时候，在求出前后两部分存在的逆序对。


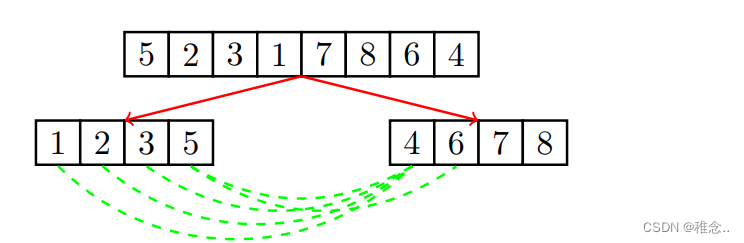
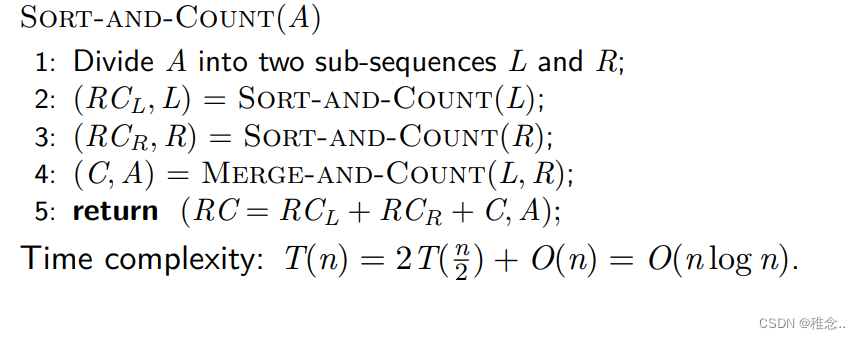
从上述图片我们可以看出，求逆序对的思想和归并排序的思想很相似，只是求逆序对时在合并的时候要再进行一步处理，也就是要求出前后两部分的逆序对。

Merge-and-Count (L, R)
1: RC = 0; i = 0; j = 0;
2: for k = 0 to ∥L∥ + ∥R∥ − 1 do
3: if L[i] > R[j] then
4: A[k] = R[j];
5: j + +;
6: RC+ = (∥L∥ − i);//这一步就说明，存在前面的数比后面的数大，也就是有逆序对。
7: if all elements in R have been copied then
8: Copy the remainder elements from L into A;
9: break;
10: end if
11: else
12: A[k] = L[i];
13: i + +;
14: if all elements in L have been copied then
15: Copy the remainder elements from R into A;
16: break;
17: end if
18: end if
19: end for