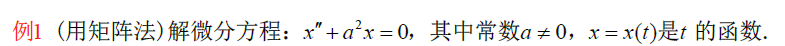5.1 神经元模型
神经网络目前使用的最广泛的定义为“神经网络是由具有适应性的简单单元组成的广泛并行互联的网络,它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。神经网络中最基本的成分是神经元模型,即上述定义的简单单元。
在生物神经网络中,每个神经元与其他神经元相连,当它兴奋时,就会向相连的神经元发送化学物质,从而改变这些神经元内的电位;如果某神经元的电位超过了阈值,那么它就会被激活,即兴奋起来,向其他神经元发送化学物质。将这种情形可以抽象为简单的M-P神经元模型。如图所示
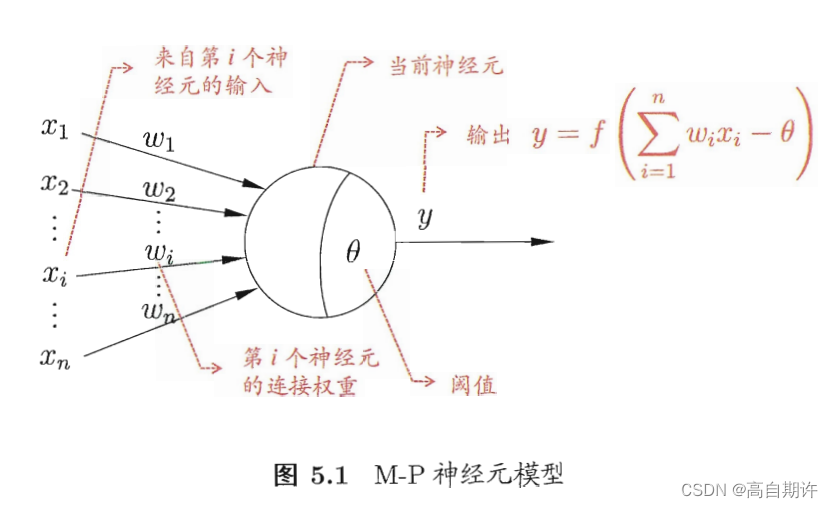
在该模型中,神经元接收到来自n个其他神经元传递过来的输入信号,这些输入信号通过带权重的连接进行传递,神经元接收到的总输入值将于神经元的阈值进行比较,然后通过激活函数处理以产生神经元的输出。
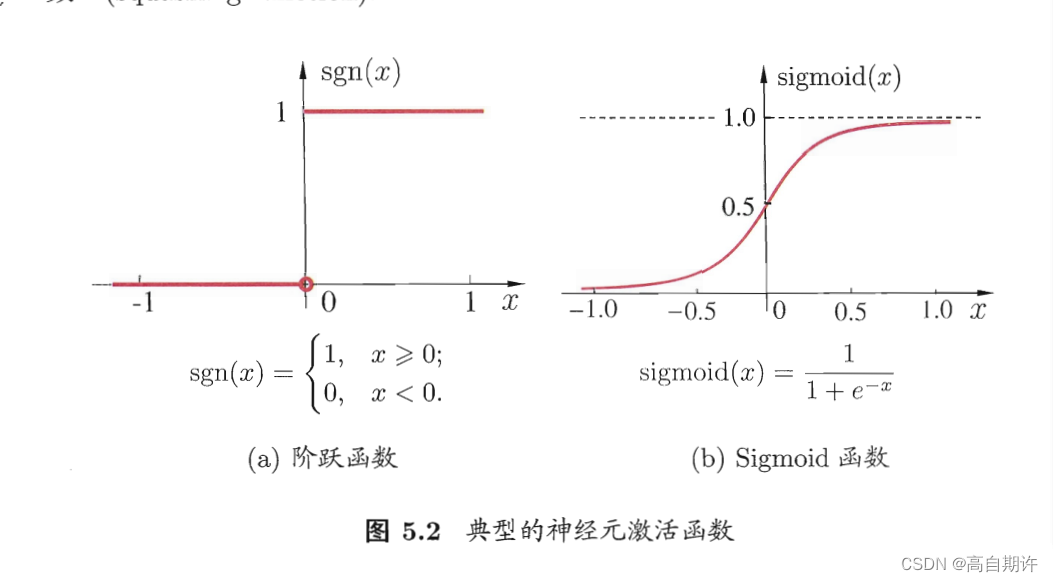
理想中的激活函数是图5.2a所示的阶跃函数,显然其具有不连续、不光滑等不太好的性质,因此实际常用Sigmoid函数作为激活函数。典型的sigmoid函数如图5.2b所示,又称为“挤压函数”。
5.2 感知机与多层网络
感知机由两层神经元组成,如图所示,输入层接受外界输入信号后传递给输出层,输出层是M-P神经元,亦称“阈值逻辑单元”。很显然,其比较容易实现与、或、非逻辑运算。
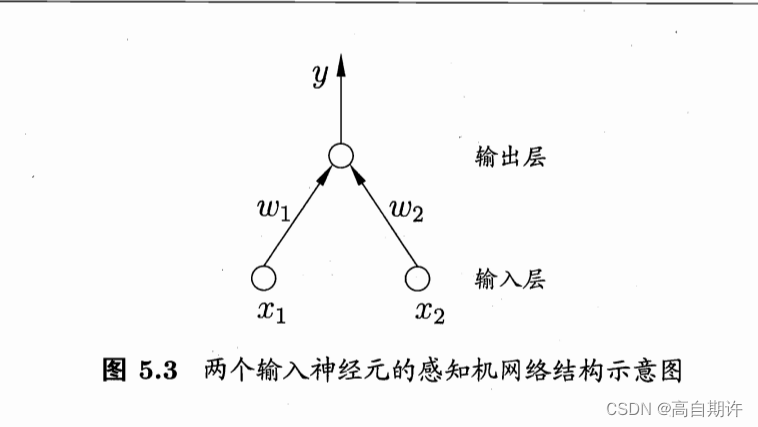

ps:感知机只有输出层神经元进行激活函数处理,即只拥有一层功能神经元,其学习能力非常有限。事实上,单层感知机只能解决线性可分的问题。
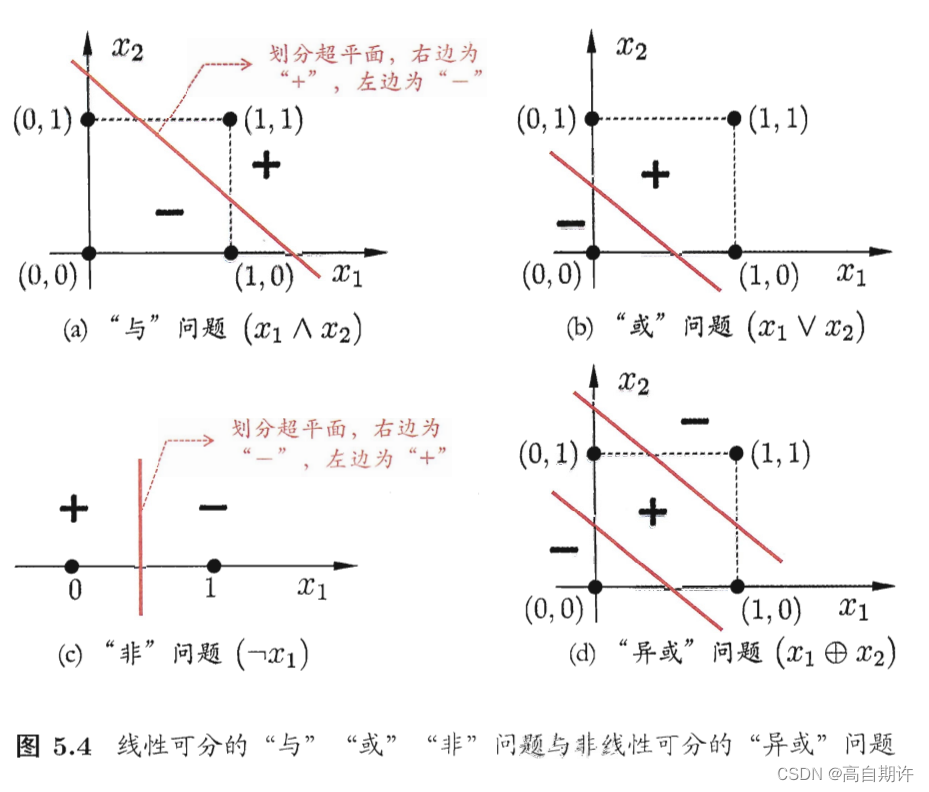
要解决非线性可分问题(例如异或问题),需考虑使用多层功能神经元。例如下图5.5中的简单两层感知机就能解决异或问题。其输出层与输入层之间的一层神经元,被称为隐层或隐含层,隐含层和输出层神经元都是拥有激活函数的功能神经元。
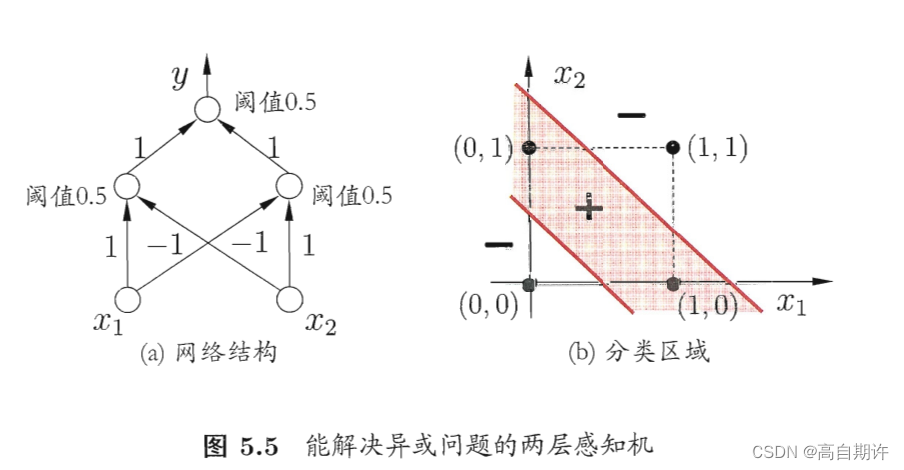
更常见的神经网络是形如下图的层级结构,每层神经元与下一层神经元全互联,神经元之间不存在同层连接也不存在跨层连接。这样的神经网络结构通常称为多层前馈前馈神经网络。
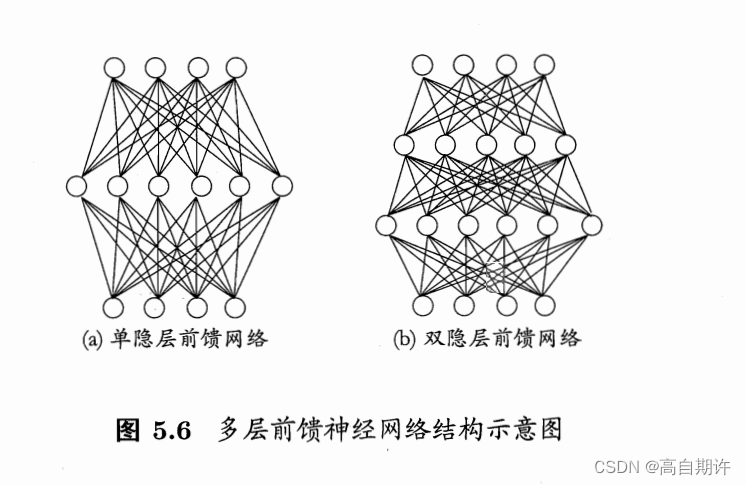
神经网络的学习过程,就是根据训练数据来调整神经元之间的连接权以及每个功能神经元的阈值;换言之,神经网络学到的东西,蕴含在连接权与阈值中。