3.6 矩阵函数求导
3.6.1 积分与求导定义
设
m
×
n
m\times n
m×n 阶矩阵
A
(
x
)
=
(
a
i
j
(
x
)
)
m
×
n
A(x)=\left(a_{ij}(x)\right)_{m\times n}
A(x)=(aij(x))m×n 中的元素都是 x 的可导函数,则
A
(
x
)
A(x)
A(x) 为关于
x
x
x 的求导为:
A
′
(
A
)
=
d
A
(
x
)
d
x
=
(
d
a
i
j
(
x
)
d
x
)
m
×
n
A'(A)=\frac{dA(x)}{dx}=\left(\frac{da_{ij}(x)}{dx}\right)_{m\times n}
A′(A)=dxdA(x)=(dxdaij(x))m×n
设
A
(
x
)
=
(
a
i
j
(
x
)
)
m
×
n
A(x)=\left(a_{ij}(x)\right)_{m\times n}
A(x)=(aij(x))m×n 的元素在区间
[
a
,
b
]
[a,b]
[a,b] 连续,在区间
[
a
,
b
]
[a,b]
[a,b] 上的积分记为
∫
a
b
A
(
x
)
d
x
=
(
a
i
j
(
x
)
d
x
)
m
×
n
\int_a^bA(x)dx=\left(a_{ij}(x)dx\right)_{m\times n}
∫abA(x)dx=(aij(x)dx)m×n
eg

3.6.2 运算性质
(1) 若 A ′ ( x ) = d A ( x ) d x ≡ 0 A'(x)=\frac{dA(x)}{dx}\equiv 0 A′(x)=dxdA(x)≡0 ⟺ \iff ⟺ A ( x ) = D ( 常 数 矩 阵 ) A(x)=D(常数矩阵) A(x)=D(常数矩阵)
(2) 求和求导:设
A
(
x
)
=
(
a
i
j
(
x
)
)
n
×
n
A(x)=(a_{ij}(x))_{n\times n}
A(x)=(aij(x))n×n ,
B
(
x
)
=
(
b
i
j
(
x
)
)
n
×
n
B(x)=(b_{ij}(x))_{n\times n}
B(x)=(bij(x))n×n 在区间
[
a
,
b
]
[a,b]
[a,b] 可到,则有
d
(
A
(
x
)
+
B
(
x
)
)
d
x
=
d
A
(
x
)
d
x
+
d
B
(
x
)
d
x
=
A
′
(
x
)
+
B
′
(
x
)
\frac{d(A(x)+B(x))}{dx}=\frac{dA(x)}{dx}+\frac{dB(x)}{dx}=A'(x)+B'(x)
dxd(A(x)+B(x))=dxdA(x)+dxdB(x)=A′(x)+B′(x)
(3) 乘积求导:
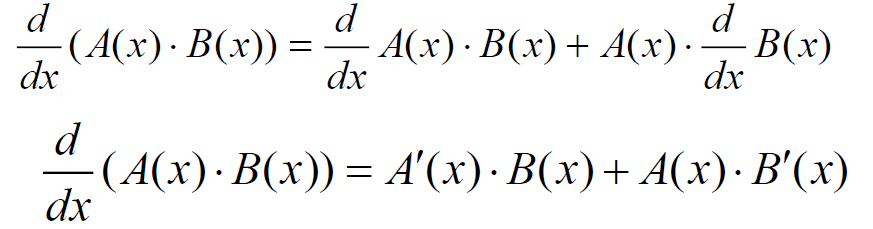
(4) 参数化:
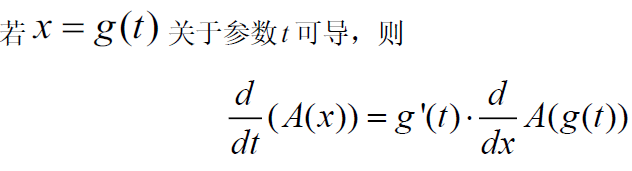
(5) 求和积分:
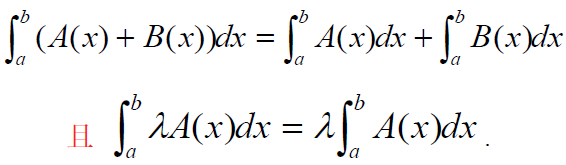
(6) 积分倍乘:
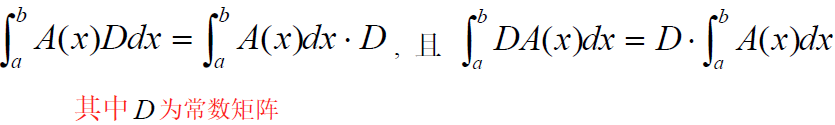
(7) 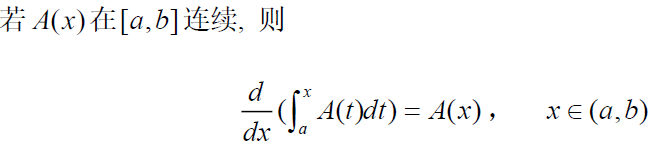
(8) N-L公式
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fGF2GRfZ-1669100960077)(10.矩阵函数/image-20221112174540714.png)]](https://img-blog.csdnimg.cn/4df9e6e59f734a6285cd3af27be570b8.png)
(9) 逆阵求导:
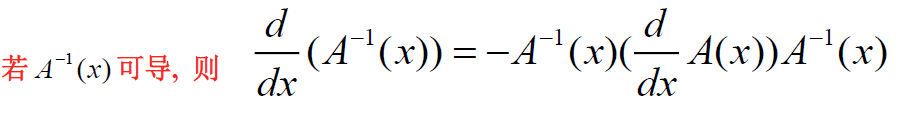
3.6.3 讨论含参阵的求导

3.6.4 3个含参矩阵函数的求导
对于三个矩阵函数
f
(
t
A
)
=
e
t
A
,
c
o
s
(
t
A
)
,
s
i
n
(
t
A
)
f(tA)=e^{tA},cos(tA),sin(tA)
f(tA)=etA,cos(tA),sin(tA) ,设方阵
A
∈
C
n
×
n
A\in C^{n\times n}
A∈Cn×n ,则有求导公式
d
e
t
A
d
t
=
A
e
t
A
d
(
s
i
n
(
t
A
)
)
d
t
=
A
c
o
s
(
t
A
)
d
c
o
s
(
t
A
)
d
t
=
−
A
s
i
n
(
t
A
)
\begin{aligned} &\frac{de^{tA}}{dt}=Ae^{tA}\\ &\frac{d(sin(tA))}{dt}=Acos(tA)\\ &\frac{dcos(tA)}{dt}=-Asin(tA) \end{aligned}
dtdetA=AetAdtd(sin(tA))=Acos(tA)dtdcos(tA)=−Asin(tA)
SP
d e − t A d t = − A e − t A d [ e − t A X ( t ) ] d t = X ′ ( t ) e − t A − A X ( t ) e − t A \begin{aligned} &\frac{de^{-tA}}{dt}=-Ae^{-tA}\\ &\frac{d[e^{-tA}X(t)]}{dt}=X'(t)e^{-tA}-AX(t)e^{-tA} \end{aligned} dtde−tA=−Ae−tAdtd[e−tAX(t)]=X′(t)e−tA−AX(t)e−tA
由欧拉公式
e t x = c o s t x + i s i n t x , e − t x = c o s t x − i s i n t x c o s ( t x ) = e i t x + e − i t x 2 , s i n ( t x ) = e i t A − e − i t A 2 i e^{tx}=costx+isintx,e^{-tx}=costx-isintx\\ cos(tx)=\frac{e^{itx}+e^{-itx}}{2},sin(tx)=\frac{e^{itA}-e^{-itA}}{2i} etx=costx+isintx,e−tx=costx−isintxcos(tx)=2eitx+e−itx,sin(tx)=2ieitA−e−itA
d c o s ( t A ) d t = 1 2 ( e i t A i A − i A e − i t A ) = i 2 2 i A ( e i t A − e − i t A ) = − e i t A − e − i t A 2 i A = − A s i n ( t A ) d s i n ( t A ) d t = 1 2 i ( e i t A i A + i A e − i t A ) = i 2 i A ( e i t A + e − i t A ) = e i t A + e − i t A 2 A = A s i n ( t A ) \frac{dcos(tA)}{dt}=\frac{1}{2}(e^{itA}iA-iAe^{-itA})=\frac{i^2}{2i}A(e^{itA}-e^{-itA})=-\frac{e^{itA}-e^{-itA}}{2i}A=-Asin(tA)\\ \frac{dsin(tA)}{dt}=\frac{1}{2i}(e^{itA}iA+iAe^{-itA})=\frac{i}{2i}A(e^{itA}+e^{-itA})=\frac{e^{itA}+e^{-itA}}{2}A=Asin(tA) dtdcos(tA)=21(eitAiA−iAe−itA)=2ii2A(eitA−e−itA)=−2ieitA−e−itAA=−Asin(tA)dtdsin(tA)=2i1(eitAiA+iAe−itA)=2iiA(eitA+e−itA)=2eitA+e−itAA=Asin(tA)
3.6.5 对于 W ( t ) = f ( t A ) W(t)=f(tA) W(t)=f(tA) 求导
若已知 W ( t ) = f ( t A ) W(t)=f(tA) W(t)=f(tA) ,两边求导 d f ( t A ) d t = d W ( t ) d t ⇒ W ′ ( t ) = A f ′ ( t A ) \frac{df(tA)}{dt}=\frac{dW(t)}{dt}\Rightarrow W'(t)=Af'(tA) dtdf(tA)=dtdW(t)⇒W′(t)=Af′(tA)
- 令 t = 0 t=0 t=0 ,可得 W ′ ( 0 ) = f ′ ( 0 ) A W'(0)=f'(0)A W′(0)=f′(0)A
若 W ( t ) = e t A W(t)=e^{tA} W(t)=etA ,两边求导 d W ( t ) d t = d ( e t A ) d t ⇒ W ′ ( t ) = A e t A \frac{dW(t)}{dt}=\frac{d(e^{tA})}{dt} \Rightarrow W'(t)=Ae^{tA} dtdW(t)=dtd(etA)⇒W′(t)=AetA
- 令 t = 0 t=0 t=0 ,可得 W ′ ( 0 ) = A W'(0)=A W′(0)=A
eg
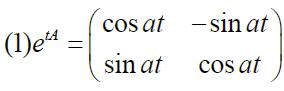
d e t A d t = ( ( c o s a t ) ′ ( − s i n a t ) ′ ( s i n a t ) ′ ( c o s a t ) ′ ) = ( − a s i n a t − a c o s a t a c o s a t − a s i n a t ) 令 t = 0 , 得 A = ( 0 − a a 0 ) \begin{aligned} &\frac{de^{tA}}{dt}=\left( \begin{matrix} (cosat)'&(-sinat)'\\(sinat)'&(cosat)' \end{matrix} \right)=\left( \begin{matrix} -asinat&-acosat\\acosat&-asinat \end{matrix} \right)\\ &令t=0,得A=\left( \begin{matrix} 0&-a\\a&0 \end{matrix} \right) \end{aligned} dtdetA=((cosat)′(sinat)′(−sinat)′(cosat)′)=(−asinatacosat−acosat−asinat)令t=0,得A=(0a−a0)
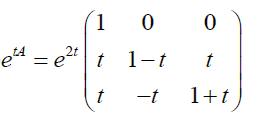
令 e t A = e 2 t B , 则 ( e t A ) ′ = ( e 2 t B ) ′ = 2 e 2 t B + e 2 t B ′ = 2 e 2 t ( 1 0 0 t 1 − t t t − t 1 + t ) + e 2 t ( 0 0 0 1 − 1 1 1 − 1 1 ) = e 2 t ( 2 0 0 2 t + 1 1 − 2 t 2 t + 1 2 t + 1 − 2 t − 1 3 + 2 t ) 由 于 ( e t A ) ′ = A e t A , 若 t = 0 , 可 得 A = ( e t A ) ′ , 代 入 的 A = ( 2 0 0 1 1 1 1 − 1 3 ) \begin{aligned} &令e^{tA}=e^{2t}B,则(e^{tA})'=(e^{2t}B)'=2e^{2t}B+e^{2t}B'=2e^{2t}\left( \begin{matrix} 1&0&0\\t&1-t&t\\t&-t&1+t \end{matrix} \right)+e^{2t}\left( \begin{matrix} 0&0&0\\1&-1&1\\1&-1&1 \end{matrix} \right)\\ &=e^{2t}\left( \begin{matrix} 2&0&0\\2t+1&1-2t&2t+1\\2t+1&-2t-1&3+2t \end{matrix} \right)\\ &由于(e^{tA})'=Ae^{tA},若t=0,可得A=(e^{tA})',代入的A=\left( \begin{matrix} 2&0&0\\1&1&1\\1&-1&3 \end{matrix} \right) \end{aligned} 令etA=e2tB,则(etA)′=(e2tB)′=2e2tB+e2tB′=2e2t⎝⎛1tt01−t−t0t1+t⎠⎞+e2t⎝⎛0110−1−1011⎠⎞=e2t⎝⎛22t+12t+101−2t−2t−102t+13+2t⎠⎞由于(etA)′=AetA,若t=0,可得A=(etA)′,代入的A=⎝⎛21101−1013⎠⎞
3.7 一阶线性常系数微分方程组
对 于 一 阶 线 性 常 系 数 微 分 方 程 , 有 { d x 1 ( t ) d t = a 11 x 1 ( t ) + ⋯ + a 1 n x n ( t ) + f 1 ( t ) ⋮ d x n ( t ) d t = a n 1 x 1 ( t ) + ⋯ + a n n x n ( t ) + f n ( t ) , 满 足 x i ( t 0 ) = c i , i = 1 , ⋯ , n 若 令 A = ( a i j ) n × n , c ⃗ = ( c 1 ⋮ c n ) , x ( t ) = ( x 1 ( t ) x 2 ( t ) ⋮ x n ( t ) ) , f ( t ) = ( f 1 ( t ) ⋮ f n ( t ) ) 可 表 示 为 { d x ( t ) d t = A x ( t ) + f ( t ) x ( t = 0 ) = c ⃗ , 其 中 f ( t ) 为 非 齐 次 项 若 f ( t ) = ( f 1 ( t ) ⋮ f n ( t ) ) = 0 ⃗ , 可 得 齐 次 微 分 方 程 , { d x ( t ) d t = A x ( t ) x ( t = 0 ) = c ⃗ \begin{aligned} &对于一阶线性常系数微分方程,有\left\{ \begin{aligned} \frac{dx_1(t)}{dt}&=a_{11}x_1(t)+\cdots+a_{1n}x_n(t)+f_1(t)\\ &\vdots\\ \frac{dx_n(t)}{dt}&=a_{n1}x_1(t)+\cdots+a_{nn}x_n(t)+f_n(t)\\ \end{aligned} \right. ,满足x_i(t_0)=c_i,i=1,\cdots,n\\ &若令A=\left(a_{ij}\right)_{n\times n},\vec{c}=\left( \begin{matrix} c_1\\\vdots\\c_n \end{matrix} \right),x(t)=\left( \begin{matrix} x_1(t)\\x_2(t)\\\vdots\\x_n(t) \end{matrix} \right),f(t)=\left( \begin{matrix} f_1(t)\\\vdots\\f_n(t) \end{matrix} \right)\\ &可表示为\left\{ \begin{aligned} &\frac{dx(t)}{dt}=Ax(t)+f(t)\\ &x(t=0)=\vec{c} \end{aligned} \right.,其中f(t)为非齐次项\\ &若f(t)=\left( \begin{matrix} f_1(t)\\\vdots\\f_n(t) \end{matrix} \right)=\vec{0},可得齐次微分方程,\left\{ \begin{aligned} &\frac{dx(t)}{dt}=Ax(t)\\ &x(t=0)=\vec{c} \end{aligned} \right. \end{aligned} 对于一阶线性常系数微分方程,有⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧dtdx1(t)dtdxn(t)=a11x1(t)+⋯+a1nxn(t)+f1(t)⋮=an1x1(t)+⋯+annxn(t)+fn(t),满足xi(t0)=ci,i=1,⋯,n若令A=(aij)n×n,c=⎝⎜⎛c1⋮cn⎠⎟⎞,x(t)=⎝⎜⎜⎜⎛x1(t)x2(t)⋮xn(t)⎠⎟⎟⎟⎞,f(t)=⎝⎜⎛f1(t)⋮fn(t)⎠⎟⎞可表示为⎩⎨⎧dtdx(t)=Ax(t)+f(t)x(t=0)=c,其中f(t)为非齐次项若f(t)=⎝⎜⎛f1(t)⋮fn(t)⎠⎟⎞=0,可得齐次微分方程,⎩⎨⎧dtdx(t)=Ax(t)x(t=0)=c
若 d A ( t ) d t = A ′ ( t ) ≡ 0 , 则 A ( t ) ≡ 0 若\frac{dA(t)}{dt}=A'(t)\equiv 0,则A(t)\equiv 0 若dtdA(t)=A′(t)≡0,则A(t)≡0
3.7.1 求解齐次方程组
a. 一阶微分
齐 次 方 程 组 d A ( t ) d t = A x 有 唯 一 解 公 式 : x = e A t c ⃗ , 即 x = e A t x ( 0 ) 齐次方程组 \frac{dA(t)}{dt}=Ax有唯一解公式:x=e^{At}\vec{c},即x=e^{At}x(0) 齐次方程组dtdA(t)=Ax有唯一解公式:x=eAtc,即x=eAtx(0)
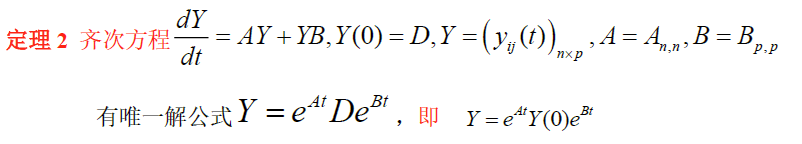
eg

( 1 ) 求 e t A A − I = ( − 4 4 2 − 2 2 1 − 2 2 1 ) = ( 2 1 1 ) ( − 2 , 2 , 1 ) , r ( A − I ) = 1 , 且 λ ( A − I ) = { − 1 , 0 , 0 } ⇒ λ ( A ) = { 0 , 1 , 1 } 对 于 2 重 根 λ 2 = 1 , 有 r ( A − I ) = 3 − 2 = 1 , 故 A 为 单 阵 A 有 谱 分 解 , A = λ 1 G 1 + λ 2 G 2 , 令 f ( x ) = e t x , f ( λ 1 ) = e 0 = 1 , f ( λ 2 ) = e t ⋅ 1 = e t , G 1 = A − λ 2 I λ 1 − λ 2 = I − A , G 2 = A − λ 1 I λ 2 − λ 1 = A e t A = f ( λ 1 ) G 1 + f ( λ 2 ) G 2 = G 1 + e t G 2 = I − A + e t A = I + ( e t − 1 ) A = ( 4 − 3 e t 4 e t − 4 2 e t − 2 2 − 2 e t 3 e t − 2 e t − 1 2 − 2 e t 2 e t − 2 2 e t − 1 ) ( 2 ) 求 齐 次 线 性 方 程 的 解 X = e t A c ⃗ = ( 4 − 3 e t 4 e t − 4 2 e t − 2 2 − 2 e t 3 e t − 2 e t − 1 2 − 2 e t 2 e t − 2 2 e t − 1 ) ( 0 1 0 ) = ( 4 e t − 4 3 e t − 2 2 e t − 2 ) ( 3 ) 代 入 t = 0 检 验 , X ( 0 ) = ( 0 1 0 ) = c ⃗ \begin{aligned} &(1)求e^{tA}\\ &A-I=\left( \begin{matrix} -4&4&2\\-2&2&1\\-2&2&1 \end{matrix} \right)=\left( \begin{matrix} 2\\1\\1 \end{matrix} \right)(-2,2,1),r(A-I)=1,且\lambda(A-I)=\{-1,0,0\}\Rightarrow \lambda(A)=\{0,1,1\}\\ &对于2重根\lambda_2=1,有r(A-I)=3-2=1,故A为单阵\\ &A有谱分解,A=\lambda_1G_1+\lambda_2G_2,令f(x)=e^{tx},f(\lambda_1)=e^{0}=1,f(\lambda_2)=e^{t\cdot1}=e^t,G_1=\frac{A-\lambda_2I}{\lambda_1-\lambda_2}=I-A,G_2=\frac{A-\lambda_1I}{\lambda_2-\lambda_1}=A\\ &e^{tA}=f(\lambda_1)G_1+f(\lambda_2)G_2=G_1+e^tG_2=I-A+e^tA=I+(e^t-1)A=\left( \begin{matrix} 4-3e^t&4e^t-4&2e^t-2\\2-2e^t&3e^t-2&e^t-1\\2-2e^t&2e^t-2&2e^t-1 \end{matrix} \right)\\ &(2)求齐次线性方程的解X=e^{tA}\vec{c}=\left( \begin{matrix} 4-3e^t&4e^t-4&2e^t-2\\2-2e^t&3e^t-2&e^t-1\\2-2e^t&2e^t-2&2e^t-1 \end{matrix} \right)\left( \begin{matrix} 0\\1\\0 \end{matrix} \right)=\left( \begin{matrix} 4e^t-4\\3e^t-2\\2e^t-2 \end{matrix} \right)\\ &(3)代入t=0检验,X(0)=\left( \begin{matrix} 0\\1\\0 \end{matrix} \right)=\vec{c} \end{aligned} (1)求etAA−I=⎝⎛−4−2−2422211⎠⎞=⎝⎛211⎠⎞(−2,2,1),r(A−I)=1,且λ(A−I)={−1,0,0}⇒λ(A)={0,1,1}对于2重根λ2=1,有r(A−I)=3−2=1,故A为单阵A有谱分解,A=λ1G1+λ2G2,令f(x)=etx,f(λ1)=e0=1,f(λ2)=et⋅1=et,G1=λ1−λ2A−λ2I=I−A,G2=λ2−λ1A−λ1I=AetA=f(λ1)G1+f(λ2)G2=G1+etG2=I−A+etA=I+(et−1)A=⎝⎛4−3et2−2et2−2et4et−43et−22et−22et−2et−12et−1⎠⎞(2)求齐次线性方程的解X=etAc=⎝⎛4−3et2−2et2−2et4et−43et−22et−22et−2et−12et−1⎠⎞⎝⎛010⎠⎞=⎝⎛4et−43et−22et−2⎠⎞(3)代入t=0检验,X(0)=⎝⎛010⎠⎞=c

令 A = ( 3 − 1 1 1 ) , X = ( x y ) , 可 写 方 程 d X d t = A X , 通 解 公 式 为 X = e t A c ⃗ , c ⃗ t = 0 = ( c 1 c 2 ) ( 1 ) A 为 行 和 矩 阵 , λ ( A ) = { 2 , t r ( A ) − 2 } = { 2 , 2 } , A − 2 I = ( 1 − 1 1 − 1 ) , r ( A − 2 I ) = 1 ≠ 2 − 2 = 0 A 不 是 单 阵 , ( A − 2 I ) 2 = 0 , 故 由 平 移 幂 0 阵 可 写 解 析 函 数 f ( x ) = f ( 2 ) + f ′ ( 2 ) ( A − 2 I ) 矩 阵 函 数 为 f ( A ) = f ( 2 ) I + f ′ ( 2 ) ( A − 2 I ) 令 f ( A ) = e t x , f ( 2 ) = e 2 t , f ′ ( 2 ) = t e 2 t , 则 e t A = e 2 t I + t e 2 t ( A − 2 I ) = e 2 t [ I + t ( A − 2 I ) ] = e 2 t [ ( 1 1 ) + ( t − t t − t ) ] = e 2 t ( 1 + t − t t 1 − t ) ( 2 ) 求 通 解 X = e t A C = e 2 t ( 1 + t − t t 1 − t ) ( c 1 c 2 ) = e 2 t ( ( 1 + t ) c 1 − t c 2 t c 1 + ( 1 − t ) c 2 ) { x = e 2 t [ ( 1 + t ) c 1 − t c 2 ] y = e 2 t [ t c 1 + ( 1 − t ) c 2 ] , c 1 , c 2 为 任 意 常 数 \begin{aligned} &令A=\left( \begin{matrix} 3&-1\\1&1 \end{matrix} \right),X=\left( \begin{matrix} x\\y \end{matrix} \right),可写方程\frac{dX}{dt}=AX,通解公式为X=e^{tA}\vec{c},\vec{c}_{t=0}=\left( \begin{matrix} c_1\\c_2 \end{matrix} \right)\\ &(1)A为行和矩阵,\lambda(A)=\{2,tr(A)-2\}=\{2,2\},A-2I=\left( \begin{matrix} 1&-1\\1&-1 \end{matrix} \right),r(A-2I)=1\neq2-2=0\\ &\quad A不是单阵,(A-2I)^2=0,故由平移幂0阵可写解析函数f(x)=f(2)+f'(2)(A-2I)\\ &\quad 矩阵函数为f(A)=f(2)I+f'(2)(A-2I)\\ &\quad 令f(A)=e^{tx},f(2)=e^{2t},f'(2)=te^{2t},则e^{tA}=e^{2t}I+te^{2t}(A-2I)=e^{2t}\left[ I+t(A-2I) \right]=e^{2t}\left[ \left( \begin{matrix} 1&\\&1 \end{matrix} \right)+\begin{aligned} \left( \begin{matrix} t&-t\\t&-t \end{matrix} \right) \end{aligned} \right]=e^{2t}\left( \begin{matrix} 1+t&-t\\t&1-t \end{matrix} \right)\\ &(2) 求通解X=e^{tA}C=e^{2t}\left( \begin{matrix} 1+t&-t\\t&1-t \end{matrix} \right)\left( \begin{matrix} c_1\\c_2 \end{matrix} \right)=e^{2t}\left( \begin{matrix} (1+t)c_1-tc_2\\tc_1+(1-t)c_2 \end{matrix} \right)\\ &\quad \left\{ \begin{aligned} &x=e^{2t}[(1+t)c_1-tc_2]\\ &y=e^{2t}[tc_1+(1-t)c_2] \end{aligned} \right.,c_1,c_2为任意常数 \end{aligned} 令A=(31−11),X=(xy),可写方程dtdX=AX,通解公式为X=etAc,ct=0=(c1c2)(1)A为行和矩阵,λ(A)={2,tr(A)−2}={2,2},A−2I=(11−1−1),r(A−2I)=1=2−2=0A不是单阵,(A−2I)2=0,故由平移幂0阵可写解析函数f(x)=f(2)+f′(2)(A−2I)矩阵函数为f(A)=f(2)I+f′(2)(A−2I)令f(A)=etx,f(2)=e2t,f′(2)=te2t,则etA=e2tI+te2t(A−2I)=e2t[I+t(A−2I)]=e2t[(11)+(tt−t−t)]=e2t(1+tt−t1−t)(2)求通解X=etAC=e2t(1+tt−t1−t)(c1c2)=e2t((1+t)c1−tc2tc1+(1−t)c2){x=e2t[(1+t)c1−tc2]y=e2t[tc1+(1−t)c2],c1,c2为任意常数
二阶微分
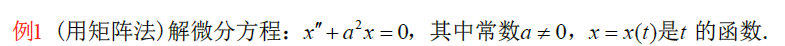
令
y
=
x
′
=
x
′
(
t
)
,
可
写
方
程
组
{
d
x
d
t
=
y
d
y
d
t
=
−
x
⟺
{
d
d
t
(
x
y
)
=
(
0
1
−
1
0
)
(
x
y
)
令
X
=
(
x
y
)
,
A
=
(
0
1
−
1
0
)
⇒
d
X
d
t
=
A
X
通
解
公
式
为
e
t
A
c
⃗
t
=
0
,
c
⃗
t
=
0
=
(
c
1
c
2
)
⇒
e
t
A
=
(
c
o
s
t
s
i
n
t
−
s
i
n
t
c
o
s
t
)
可
知
X
=
e
t
A
C
=
(
c
o
s
t
s
i
n
t
−
s
i
n
t
c
o
s
t
)
(
c
1
c
2
)
=
(
c
1
c
o
s
t
+
c
2
s
i
n
t
c
2
c
o
s
t
−
c
1
s
i
n
t
)
,
故
原
方
程
通
解
x
=
c
1
c
o
s
t
+
c
2
s
i
n
t
\begin{aligned} &令y=x'=x'(t),可写方程组\left\{ \begin{aligned} &\frac{dx}{dt}=y\\ &\frac{dy}{dt}=-x \end{aligned} \right.\iff \left\{ \frac{d}{dt}\left( \begin{matrix} x\\y \end{matrix} \right) \right.=\left( \begin{matrix} 0&1\\-1&0 \end{matrix} \right)\left( \begin{matrix} x\\y \end{matrix} \right)\\ &令X=\left( \begin{matrix} x\\y \end{matrix} \right),A=\left( \begin{matrix} 0&1\\-1&0 \end{matrix} \right)\Rightarrow \frac{dX}{dt}=AX\\ &通解公式为 e^{tA}\vec{c}_{t=0},\vec{c}_{t=0}=\left( \begin{matrix} c_1\\c_2 \end{matrix} \right)\Rightarrow e^{tA}=\left( \begin{matrix} cost&sint\\-sint&cost \end{matrix} \right)\\ &可知X=e^{tA}C=\left( \begin{matrix} cost&sint\\-sint&cost \end{matrix} \right)\left( \begin{matrix} c_1\\c_2 \end{matrix} \right)=\left( \begin{matrix} c_1cost+c_2sint\\c_2cost-c_1sint \end{matrix} \right),故原方程通解x=c_1cost+c_2sint \end{aligned}
令y=x′=x′(t),可写方程组⎩⎪⎪⎨⎪⎪⎧dtdx=ydtdy=−x⟺{dtd(xy)=(0−110)(xy)令X=(xy),A=(0−110)⇒dtdX=AX通解公式为etAct=0,ct=0=(c1c2)⇒etA=(cost−sintsintcost)可知X=etAC=(cost−sintsintcost)(c1c2)=(c1cost+c2sintc2cost−c1sint),故原方程通解x=c1cost+c2sint
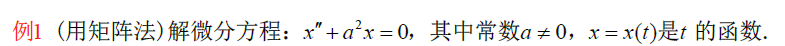
x ′ ′ = − a 2 x , 令 { x ′ = a y ( t ) y ′ ( t ) = − a x ( a y ′ ( t ) = − a 2 x = x 2 ) , 即 d X d t = A X , A = { 0 a − a 0 } , X = ( x y ) 通 解 为 X = e t A C , 其 中 e t A = e ( 0 a t − a t 0 ) = ( c o s a t s i n a t − s i n a t c o s a t ) , 设 C = ( c 1 c 2 ) X = e t A C = ( c o s a t s i n a t − s i n a t c o s a t ) ( c 1 c 2 ) = ( c 1 c o s a t + c 2 s i n a t c 2 c o s a t − c 1 s i n a t ) \begin{aligned} &x''=-a^2x,令\left\{ \begin{aligned} &x'=ay(t)\\ &y'(t)=-ax&(ay'(t)=-a^{2}x=x^2) \end{aligned} \right.,即\frac{dX}{dt}=AX,A=\left\{ \begin{matrix} 0&a\\-a&0 \end{matrix} \right\},X=\left( \begin{matrix} x\\y \end{matrix} \right)\\ &通解为 X=e^{tA}C,其中e^{tA}=e^{\left( \begin{matrix} 0&at\\-at&0 \end{matrix} \right)}=\left( \begin{matrix} cosat&sinat\\-sinat&cosat \end{matrix} \right),设C=\left( \begin{matrix} c_1\\c_2 \end{matrix} \right)\\ &X=e^{tA}C=\left( \begin{matrix} cosat&sinat\\-sinat&cosat \end{matrix} \right)\left( \begin{matrix} c_1\\c_2 \end{matrix} \right)=\left( \begin{matrix} c_1cosat+c_2sinat\\ c_2cosat-c_1sinat \end{matrix} \right) \end{aligned} x′′=−a2x,令{x′=ay(t)y′(t)=−ax(ay′(t)=−a2x=x2),即dtdX=AX,A={0−aa0},X=(xy)通解为X=etAC,其中etA=e(0−atat0)=(cosat−sinatsinatcosat),设C=(c1c2)X=etAC=(cosat−sinatsinatcosat)(c1c2)=(c1cosat+c2sinatc2cosat−c1sinat)