串、数组和广义表
顺序表和链表分别是线性表的两种存储结构。
栈和队列是操作受限的线性表。
串、数组和广义表是内容受限的线性表。
1. 串
1.1 串的概念和结构
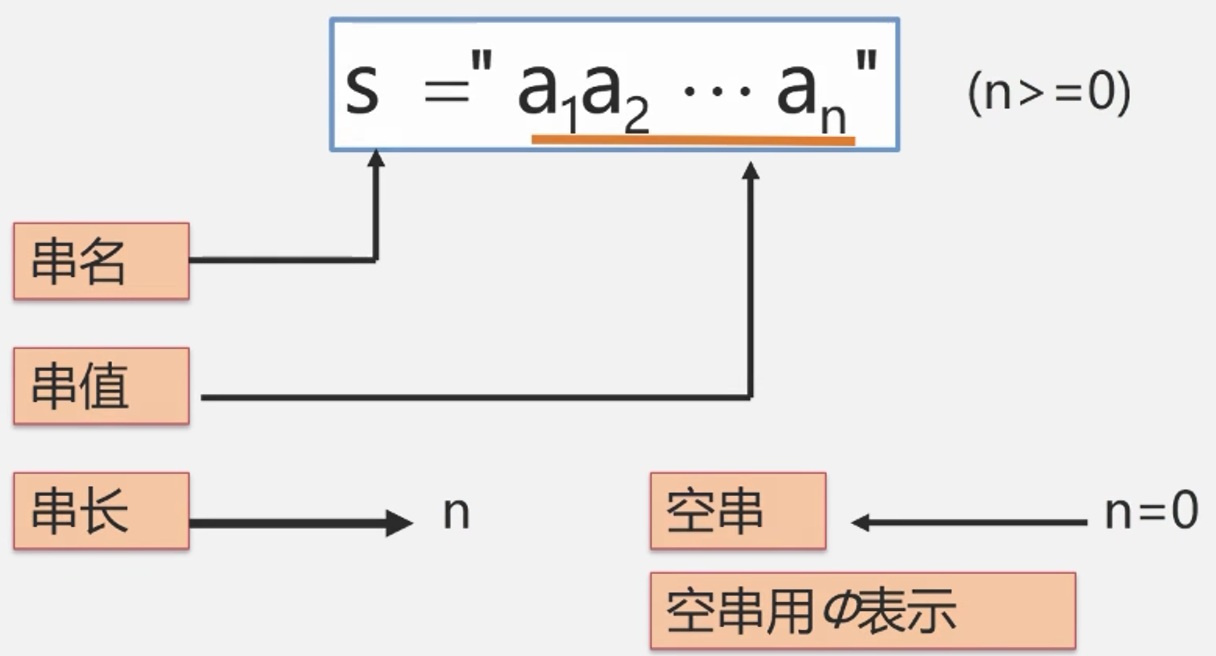
串(String)—零个或多个任意字符组成的有限序列
所谓串是内容受限的线性表。就是要求该线性表的元素类型只能是字符型,而一般的线性表元素任意。串的逻辑结构如下:
- 子串:一个串中任意个连续字符组成的子序列(含空串)称为该串的子串。
- 真子串:是指不包含自身的所有子串。
- 主串:包含子串的串称为主串
- 字符位置:字符在序列中的序号为该字符在串中的位置
- 子串位置:子串第一个字符在主串中的位置
- 空格串:有一个或多个空格组成的串,与空串不同
- 串相等:串长相等且对应位置字符相等(空串都相等)
串作为内容受限的线性表,同样有两种存储结构,串的顺序存储结构叫顺序串,串的链式存储结构叫链串。当然有顺序存储就会相应的有静态串和动态串
1.2 顺序串和链串
-
顺序串
其实就是顺序表中数据元素改成char类型,按空间分配类型可分为静态顺序串和动态顺序串,下面是静态顺序串定义:
//顺序串 #define MAXSIZE 255 struct SString { char ch[MAXSIZE+1];//下标范围0~MAXSIZE //0号下标元素默认不用,这样在一些算法中能带来简便 int length;//当前串的长度 };相比链串,由于实际中很少队串进行插入删除操作,所以顺序串的使用更加广泛。对于串的特殊运算,后面会讲解。但顺序串的一些基本操作可参考这篇文章:
[(243条消息) 【数据结构笔记】- 顺序表_Answer-2296的博客-CSDN博客_数据结构顺序表的总结](
https://blog.csdn.net/weixin_63267854/article/details/124453493?spm=1001.2014.3001.5501)
-
链串
结点数据于存储字符,指针域串联字符形成串。
使用何种类型的链表,则根据具体情况,赋予链表不同性质:单向,双向,带头,不带头,循环,非循环。
相比于顺序串,链串操作方便(优点),但存储密度较低(缺点,链式存储通病)

如果一个结点数据域只存储一个字符,存储密度就是20%,很低!如下

为了提高存储密度,一个结点数据域存储多个字符,提高存储密度的同时,保留链串操作的简便性

相应的结点中存储字符的那一部分称为“块”,相应的我们将串的链式存储结构称为块链结构
下面为块链结构的定义
//链串 #define CHUNKSIZE 80 struct Chunk { char ch[CHUNKSIZE]; Chunk* next; }; struct LString { Chunk* head, * tail;//串的头指针和尾指针 int curlen;//串当前长度 };//块链结构对于串的特殊运算,后面会讲解。但链串的一些基本操作可参考这篇文章:
(243条消息) 【数据结构笔记】- 链表 - 基础到实战-入门到应用_Answer-2296的博客-CSDN博客
1.3 BF算法–串的模式匹配法之一
串的模式匹配算法:确定主串中所含子串(模式串)第一次出现的位置(定位)。应用于搜索引擎、拼写检查等,常见的算法有BF算法和KMP算法
BF算法(Brute-Force),采用穷举法的思路。就是从主串S第一个字符一次与T的字符进行匹配。具体实现如下
//匹配成功,返回模式串p在文本串s中的位置,否则返回-1
int ViolentMatch(char* s, char* p)
{
int sLen = strlen(s);
int pLen = strlen(p);
int i = 0;
int j = 0;
while (i < sLen && j < pLen)
{
if (s[i] == p[j])
{
//如果当前字符匹配成功(即S[i] == P[j]),则i++,j++
i++;
j++;
}
else
{
//如果失配(即S[i]! = P[j]),i回溯即令i = i - (j - 1),j重新开始:j = 0
i = i - j + 1;//相当于刚才移动了j-0个字符,现在回溯就是i-j+0,但该位置比过了,所以比对i-j+1
j = 0;
}
}
//匹配成功,返回模式串p在文本串s中的位置,否则返回-1
if (j == pLen)
return i - j;
else
return -1;
}
BF算法简单,代码凝练
-
BF算法的时间复杂度
假设主串长度为n,模式串的长度为m。则BF算法的最好时间复杂度为
m,最坏时间复杂度为(n-m+1)*m。
1.5 KMP算法–串的模式匹配法之一
以下算法按照C++中的字符串string讲解(字符数组从0开始计数,有些字符数组从1开始计数,算法差异后续讲解,但实质未变)
KMP算法由Donald Knuth、Vaughan Pratt、James H. Morris三人于1977年联合发表,故取这3人的姓氏命名此算法。
KMP算法充分利用部分已经匹配的结果加快串的模式匹配。
KMP算法思路讲解:用下标i遍历主串且不回溯,比对的模式串下标j在失配是遵守next[j]数组回溯。(next[j]是一个数组,按照特定规则计算得到的模式串下标j回溯的位置)KMP算法时间复杂度为O(n+m)。
- KMP算法概述
KMP算法的核心在于数组next[j],模式串中每一个字符都在next数组中有唯一对应值,该值表示主串和模式串字符不匹配时模式串下标
j回溯的位置,具体next[j]如何的来和KMP算法为何可以这样回溯在后文有讲解,这里先接受有这样一个next数组。以下是KMP算法实现
- kmp算法和BF算法区别就在于主串i不回溯,子串j按照next[j]来回溯(后面会介绍会什么可以这样回溯!)
KMP算法实现如下:
int KmpSearch(char* s, char* p) { int i = 0; int j = 0; int sLen = strlen(s); int pLen = strlen(p); while (i < sLen && j < pLen) { //如果j = -1说明前一轮字符匹配失败主串后移,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++ if (j == -1 || s[i] == p[j]) { i++; j++; } else { //如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j] //next[j]即为j所对应的next值 j = next[j]; } } if (j == pLen)//说明匹配成功 return i - j;//返回下标 else return -1; }
了解了KMP算法,下面讲解next数组
1.5.1 next数组
首先了解串中的两个概念,对于一个串P=P1P2P3…Pj-1Pj,对于下标j而言有
- 前缀:串P中包含P1的子串,但不包括串P本身
- 后缀:串P中包含Pj的子串,但不包括串P本身
next数组的作用
KMP的next 数组相当于告诉我们:当模式串中的某个字符跟文本串中的某个字符匹配失配时,模式串下一步应该跳到哪个位置。如模式串中在j 处的字符跟文本串在i 处的字符匹配失配时,下一步用next [j] 处的字符继续跟文本串i 处的字符匹配
按步求解next数组
-
寻找模式串前缀后缀的最长公共元素长度
对于 P = P0P1 … Pj-1 Pj,寻找模式串P中长度最大且相等的前缀和后缀。如果存在 P0P1 …Pk-1Pk = Pj-kPj-k+1…Pj-1Pj,那么在包含 Pj 的模式串中有最大长度为k+1的相同前缀后缀。就是寻找寻找模式串前缀后缀的最长公共元素长度,这里以模式串“abab”为例子,得到一个数组:

-
将上一步数组整体右移一位,最右边截断,最左边补-1得到的数组就是next数组了(世界上next[j]就是P = P0P1 … Pj-1 的相等前后缀的最长长度,而对于第一个没有j-1字符,就设置为最小下标-1,其实这是个无用的值,在后续算法中只是作为一个标识而已)

-
根据next数组匹配
当主串和模式串字符失配时,模式串下标j则向左移动j-next[j],对应下标也就是j=j-(j-next[j])=next[j]。所以当主串和模式串字符失配时,j=next[j]。

按next数组回溯产生的效果
主串下标i不用回溯,模式串下标j部分回退,提高效率。
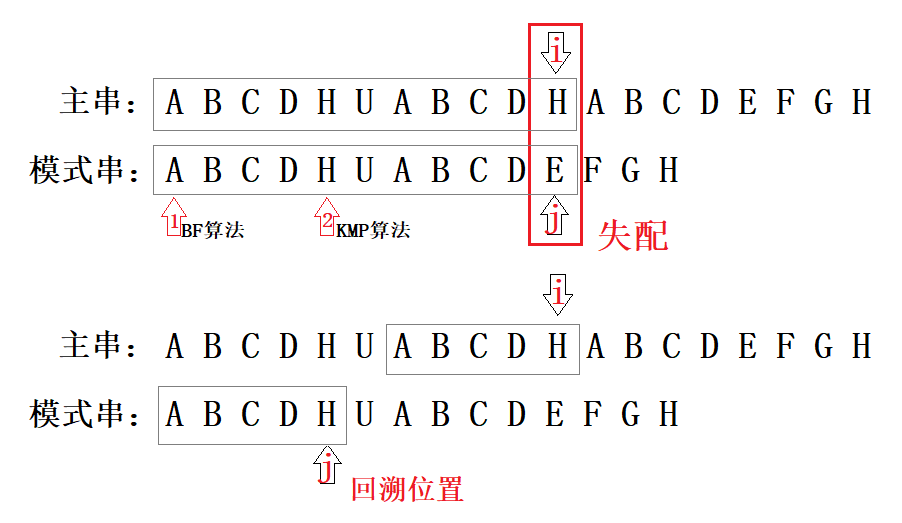
下图主串和模式串匹配好的字符时灰色框:ABCDHUABCD,但图中可以看到下一次比对中H和E失配了,那么模式串j回溯到哪?
按next数组回溯到下面那副图中也就是H。这时主串和模式串中匹配好的字符并非从零开始,而是新的灰色框:ABCD,也印证那句话:KMP算法充分利用部分已经匹配的结果加快串的模式匹配。
那么为什么next数组能产生如此效果?为什么KMP算法主串下标不用回退?
首先回答第二个问题,为什么主串下标可以不回退?担心这个问题的伙伴无非顾虑的是担心主串和模式串失配时,主串下标不回溯会不会遗漏和模式串匹配的字符?答案是不会!
因为有next数组!next数组求解的就是失配下标前的相等的前后缀最大长度,也就是失配后主串下标前能和模式串从头开始匹配多少个字符?上面的图中H和E失配后主串前面ABCD便能和模式串中的ABCD匹配,这样的工作已经在求解next数组的时候完成了,所以主串下标是无需回退的。
回到求解next数组那一步,核心时求解相等前缀后缀的最大长度!求解next[j]也就是求解模式串钱j-1个元素的相等前后缀的最大长度,这里设最大长度为length,直接next[j]=length。length对应的下标刚好就是刚才求解得到的最大前缀的下一个字符,所以主串和模式串失配时,j=next[j],下一步主串和模式串比对的字符前面的就是新的前缀和后缀了,在上图对应的新前后缀就是ABCD了,所以说KMP算法利用了已匹配字符序列,让i不回溯,j减少回溯。提高效率。
1.5.2 递推求next数组
这里先给出代码实现
void GetNext(char* p,int next[])
{
int pLen = strlen(p);
next[0] = -1;
int k = -1;
int j = 0;
while (j < pLen - 1)//只需要遍历到倒数第二个元素
{
//p[k]表示前缀,p[j]表示后缀
if (k == -1 || p[j] == p[k])
{
++k;
++j;
next[j] = k;
}
else
{
k = next[k];
}
}
}
核心:根据next[i]前面的数值求解next[i]
这里用到的两个下标,j时上一层循环的最大前缀的下一个字符的下标,i表示上一层循环得最大后缀得下一个,也就是待求得next数组下标。不理解这句话最好的解决办法就是,写出循环每一次对ij修改的情况,并观察模式串对应位置。算法种初值设置有讲究,后面会讲。初值设定:next[0] = -1; int k = -1; int j = 0;设模式串为T。
i作为遍历模式串的下标,循环中比较p[i]是否等于p[j],会分三种情况
-
当p[i] == p[j],回看这句话:j时上一层循环的最大前缀的下一个字符的下标,i表示上一层循环得最大后缀的下一个,p[i] == p[j]说明上一个前后缀往后延一个,前后缀任然相等,就直接赋值了next[i] = j;
-
当p[i] != p[j],就令j=next[j];寻找长度更短的相同前缀后缀。
为何递归前缀索引j=next[j],就能找到长度更短的相同前缀后缀呢?
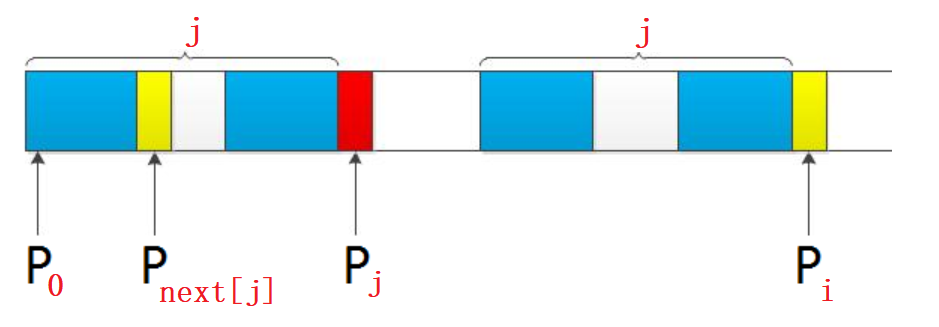
我们拿前缀 p0…pj-1 pj 去跟后缀pi-j…pi-1 pi匹配,如果pk 跟pj 失配,下一步就是用p[next[k]] 去跟pj 继续匹配,如果p[ next[k] ]跟pj还是不匹配,则需要寻找长度更短的相同前缀后缀,即下一步用p[ next[ next[k] ] ]去跟pj匹配。此过程相当于模式串的自我匹配,所以不断的递归k = next[k],直到要么找到长度更短的相同前缀后缀,要么没有长度更短的相同前缀后缀,也就是第三种情况了。
-
j == -1,出现j == -1说明已经没有字符和p[i]比较了,也就是无法找到更短的前后缀了。直接令next[i]=0或者next[i]=++j。如此一来,主串和模式串失配时,模式串回溯到next[i]也就是0,就是从头开始比对,因为没有相等得前后缀了嘛。
出现j == -1情况有两情况,一种时初值j == -1,另一种就是在循环中不断寻找更小得前后缀时(j=next[j]),所要找的前后缀不断缩小,直到没有,此时对应j == -1。
初值设定很讲究
next[0] = -1;
int j = -1;
int i = 0;
将next数组第一个元素和j均设置为next数组最小下标减1的值。i设置成next数组最小下标。为什么我这里强调是最小下标减1?因为一些串结构中的0号位置是不存储数据的!这样的串在求next数组时的初值就不能照搬了。因为串的下标的标准不一样,对应的next数组时不一样的。相同的字符对应的数组值回相差串最小下标之差。如对于串首元素下标为0和串下标首元素为1的next数组如下:
但我们在求解next数组的时候,在初值上做了区别,具体实现上使用递归,规避了求解next数组的差异性,使得不同标准的串都能用这一套算法求解!
回过来,都知道-1在数组中是无效下标,那next[0]和j初始值为什么不能设置成-5?其他无效下标呢?答案是当然可以啦,只是在kmp算法实现时需做特殊处理。解释钱
先看next[0]和j初值为1的算法
int KmpSearch(char* s, char* p)
{
int i = 0;
int j = 0;
int sLen = strlen(s);
int pLen = strlen(p);
while (i < sLen && j < pLen)
{
//如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++
if (j == -1 || s[i] == p[j])
{
i++;
j++;
}
else
{
//如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]
//next[j]即为j所对应的next值
j = next[j];
}
}
if (j == pLen)
return i - j;
else
return -1;
}
值得注意当j == -1时,也就是下标无效时,kmp算法中让主串i,j均自增,使得j回归正常的模式串最小下标了,主串字符也后移动一个了。简单的加1回归正常值,就是初值设定的妙处。如果next[0]=-5,j=-5不仅是kmp算法,而且是求解next数组的代码在j==-5时都需要单独对j和i赋值,使得下标回归正常值。所以这样的初值设定使得代码最具整洁性。
某专家博主说,next数组有些像状态机,笔者认为很有道理:
next 负责把模式串向前移动,且当第j位不匹配的时候,用第next[j]位和主串匹配,就像打了张“表”。此外,next 也可以看作有限状态自动机的状态,在已经读了多少字符的情况下,失配后,前面读的若干个字符是有用的。
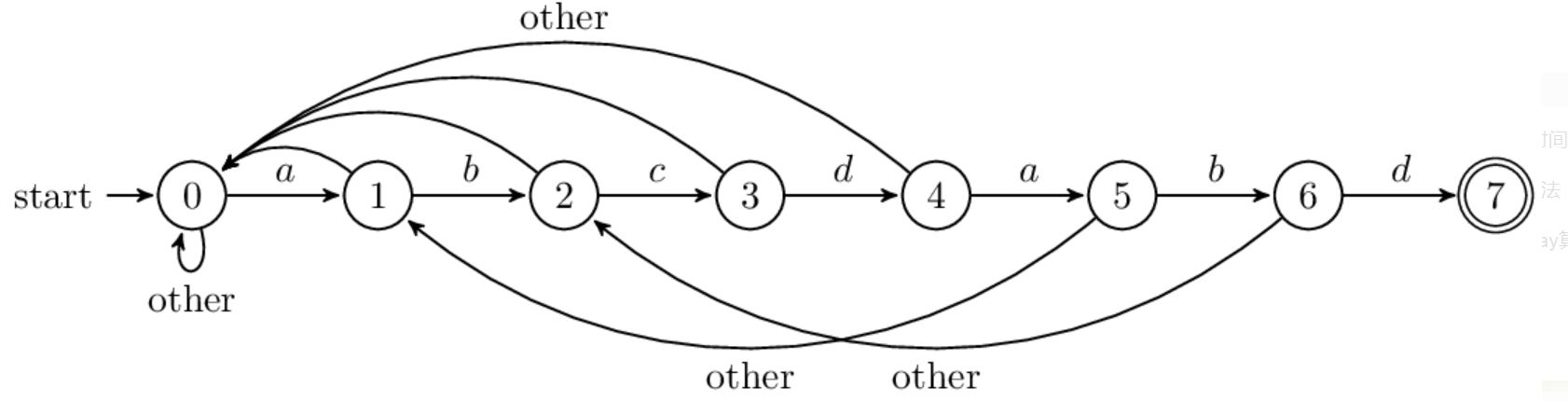
以上便是KMP算法了,不得不敬佩那三位科学家,牛掰的
KMP算法完整实现
//求next数组
void GetNext(char* p,int next[])
{
int pLen = strlen(p);
next[0] = -1;
int k = -1;
int j = 0;
while (j < pLen - 1)
{
//p[k]表示前缀,p[j]表示后缀
if (k == -1 || p[j] == p[k])
{
++k;
++j;
next[j] = k;
}
else
{
k = next[k];
}
}
}
//模式匹配
int KmpSearch(char* s, char* p)
{
int i = 0;
int j = 0;
int sLen = strlen(s);
int pLen = strlen(p);
while (i < sLen && j < pLen)
{
//如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++
if (j == -1 || s[i] == p[j])
{
i++;
j++;
}
else
{
//如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]
//next[j]即为j所对应的next值
j = next[j];
}
}
if (j == pLen)
return i - j;
else
return -1;
}
1.5.3 next数组的优化
这里引入一个串最小下标为1(前面聊过不同的串标准next数组的差异)的模式串对应的next数组:
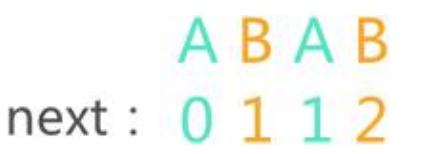
该模式串:第一个字符和第三个字符都是 ‘A’,它们对应的 next 值分别是 0 和 1;同样,第二个字符和第四个字符都是 ‘B’,它们对应的 next 值分别是 1 和 2。
第 3 个字符 ‘A’ 对应的 next 值是 1,意味着当该字符导致模拟匹配失败后,下次匹配会从模式串的第 1 个字符’A’ 开始。那么问题来了,第一次模式匹配失败说明模式串中的 ‘A’ 和主串对应的字符不相等,那么下次用第 1 个字符 ‘A’ 与该字符匹配,也绝不可能相等。
同样的道理,第 4 个字符 ‘B’ 对应的 next 值是 2,意味着当该字符导致模式匹配失败后,下次模式匹配会从模式串第 2 个字符 ‘B’ 开始,这次匹配也绝不会成功。可以说这里做了些无用功。所以我们就思考如何优化next数组?
每次给next数组赋值前,当前字符和回溯后的字符是否相等!实现如下:
//优化过后的next 数组求法
void GetNextval(char* p, int next[])
{
int pLen = strlen(p);
next[0] = -1;
int k = -1;
int j = 0;
while (j < pLen - 1)
{
//p[k]表示前缀,p[j]表示后缀
if (k == -1 || p[j] == p[k])
{
++j;
++k;
//较之前next数组求法,改动在下面4行
if (p[j] != p[k])
next[j] = k; //之前只有这一行
else
//因为不能出现p[j] = p[ next[j ]],所以当出现时需要继续递归,k = next[k] = next[next[k]]
next[j] = next[k];
}
else
{
k = next[k];
}
}
}
相同的三元组以列标做升序排序。
#include<stdio.h>
#define NUM 10
//三元组
typedef struct {
int i, j;
int data;
}triple;
//三元组顺序表
typedef struct {
triple data[NUM];
int mu, nu, tu;
}TSMatrix;
//稀疏矩阵的转置
void transposeMatrix(TSMatrix M, TSMatrix* T) {
//1.稀疏矩阵的行数和列数互换
(*T).mu = M.nu;
(*T).nu = M.mu;
(*T).tu = M.tu;
if ((*T).tu) {
int col, p;
int q = 0;
//2.遍历原表中的各个三元组
for (col = 1; col <= M.nu; col++) {
//重复遍历原表 M.m 次,将所有三元组都存放到新表中
for (p = 0; p < M.tu; p++) {
//3.每次遍历,找到 j 列值最小的三元组,将它的行、列互换后存储到新表中
if (M.data[p].j == col) {
(*T).data[q].i = M.data[p].j;
(*T).data[q].j = M.data[p].i;
(*T).data[q].data = M.data[p].data;
//为存放下一个三元组做准备
q++;
}
}
}
}
}
int main() {
int i, k;
TSMatrix M, T;
M.mu = 3;
M.nu = 2;
M.tu = 4;
M.data[0].i = 1;
M.data[0].j = 2;
M.data[0].data = 1;
M.data[1].i = 2;
M.data[1].j = 2;
M.data[1].data = 3;
M.data[2].i = 3;
M.data[2].j = 1;
M.data[2].data = 6;
M.data[3].i = 3;
M.data[3].j = 2;
M.data[3].data = 5;
for (k = 0; k < NUM; k++) {
T.data[k].i = 0;
T.data[k].j = 0;
T.data[k].data = 0;
}
transposeMatrix(M, &T);
for (i = 0; i < T.tu; i++) {
printf("(%d,%d,%d)\n", T.data[i].i, T.data[i].j, T.data[i].data);
}
return 0;
2. 数组
编程语言中都提供有数组这种数据类型,比如 C/C++、Java 等。但本节我要讲解的不是作为数据类型的数组,而是数据结构中提供的一种叫数组的存储结构
数组是相同数据类型的集合,是线性表,用于存储一对一的数据。数组最大的特点就是结构固定–定义后维数和维界不再改变。我们经常选用顺序存储结构(顺序表)来实现数组,而不用链式结构(链表)。
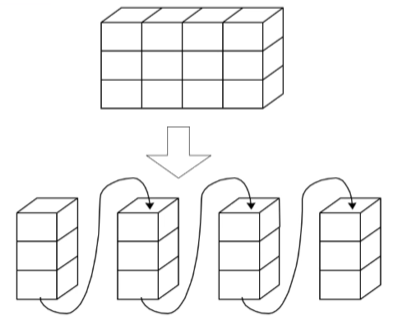
数组可以是多维的,但存储数据元素的内存单元地址是一维的。n维数组就是n-1维数组的元素任然是一维数组,由此可见多位数组实际就是一维数组不断累加而来的。
2.1 数组的内存存储
数组可以是多维的,而顺序表只能是一维的线性空间。要想将 N 维的数组存储到顺序表中,可以采用以下两种方案:
以列序为主(先列后行):按照行号从小到大的顺序,依次存储每一列的元素;
以行序为主(先行后序):按照列号从小到大的顺序,依次存储每一行的元素。
-
一维数组的内存存储
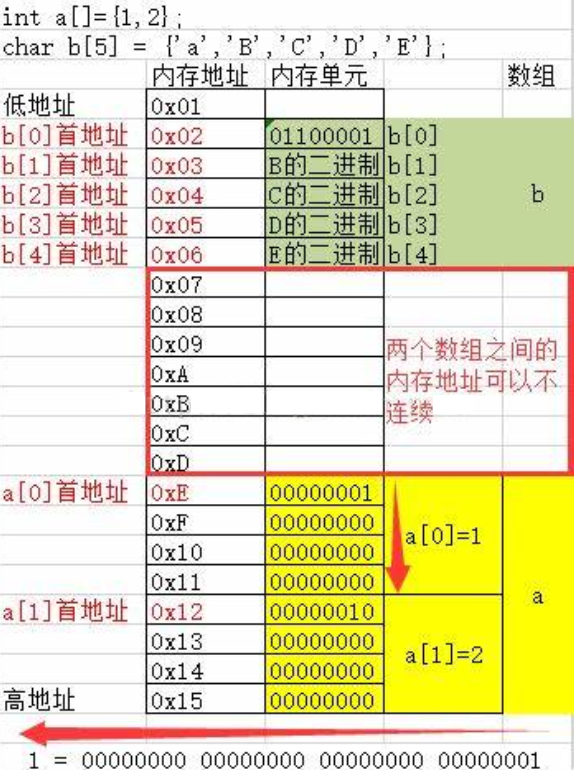
-
二维数组的内存存储
按行序为主序或列序为主序分为两种存储方式,多用行序为主序
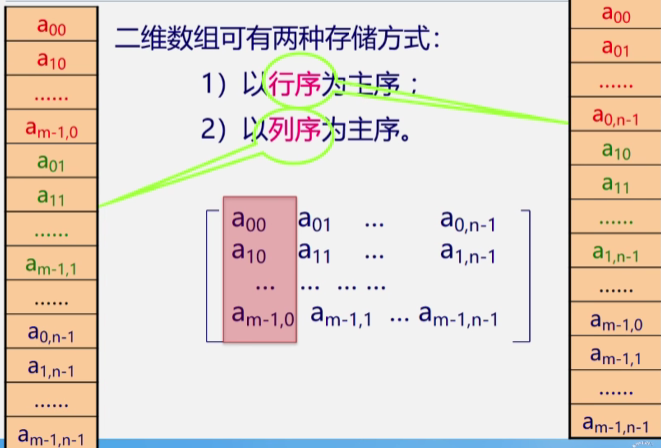
以行序为主序的数组:
设数组开始存储位置
LOC( 0,0),存储每个元素需要L个存储单元数组元素a[i][j]的存储位置是:``LOC( i , j)= LOC(o,0)+(n*i+j)*L`也就是首地址加上
a[i][j]前面所有元素个数,即为a[i][j]地址位置 -
三维数组的内存存储
按页列行存放,页优先的顺序存储
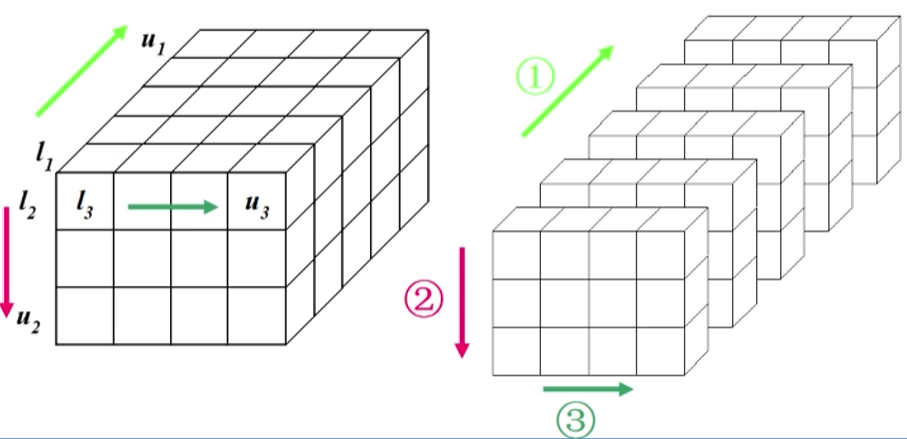
a[m1][m2] [m3]各维元素个数为m, m2, m3(页,行,列)
下标为i1, i2 i3(页,行,列)的数组元素的存储位置:

也就是首地址加上
a[i][j]前面所有元素个数,即为a[i][j]地址位置 -
n维数组的内存存储

各维数个数维m1,m2…mn的n维数组:
L O C ( i 1 , I 2 , . . . , i n ) = a + ∑ j = 1 n − 1 i j ∗ ∏ k = j + 1 n m k + i n LOC(i_1,I_2,...,i_n)=a+\sum_{j=1}^{n-1}{i_j}*{\prod_{k=j+1}^{n}{m_k}}+i_n LOC(i1,I2,...,in)=a+j=1∑n−1ij∗k=j+1∏nmk+in
理解:在n维数组中求某个元素位置:就是求该元素前面有多少个元素+首地址
2.2 特殊矩阵
矩阵对元素随机存取的特性就要求我们要用数组存储它,数组存储矩阵的存储密度为1。
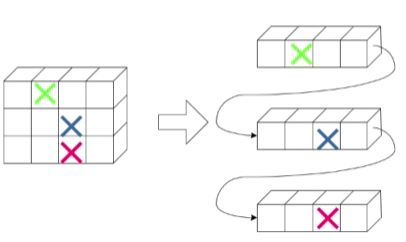
对特殊矩阵我们用一维数组存储特殊矩阵,对相同元素值只分配一个元素空间,对零元素不分配空间,达到矩阵压缩的目的。这里所说的特殊矩阵,主要分为以下两类:
含有大量相同数据元素的矩阵,比如对称矩阵;
含有大量 0 元素的矩阵,比如稀疏矩阵、上(下)三角矩阵;
2.2.1 对称矩阵
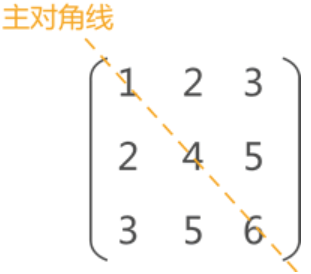
矩阵中有两条对角线,其中图 中的对角线称为主对角线,另一条从左下角到右上角的对角线为副对角线。对称矩阵指的是各数据元素沿主对角线对称的矩阵。
结合数据结构压缩存储的思想,我们可以使用一维数组存储对称矩阵。由于矩阵中沿对角线两侧的数据相等,因此数组中只需存储对角线一侧(包含对角线)的数据即可。
对于n维数组,二维数组存储需n2个存储空间,但矩阵压缩用一维数组只需要n(n+1)/2个元素空间。
对称矩阵压缩:将对称矩阵的下三角矩阵(或上三角矩阵)以行序为主序展开存在一维数组中

原对称矩阵中下三角矩阵元素a[i][j]在一维数组中位置(以下三角为例):
k
=
i
(
i
−
1
)
2
+
j
+
a
/
/
a
是
一
维
数
组
首
地
址
k=\frac{i(i-1)}{2}+j+a//a是一维数组首地址
k=2i(i−1)+j+a//a是一维数组首地址
而原上三角矩阵元素a[i][j]在一维数组中的位置(对应到下三角矩阵的元素即为a[j][i],高中知识)
k
=
j
(
j
−
1
)
2
+
i
+
a
/
/
a
是
一
维
数
组
首
地
址
k=\frac{j(j-1)}{2}+i+a//a是一维数组首地址
k=2j(j−1)+i+a//a是一维数组首地址
就是首地址加上a[i][j]前面所有元素个数,即为a[i][j]地址位置
2.2.2 上(下)三角矩阵
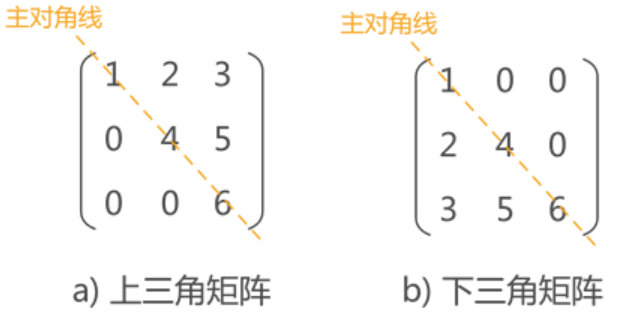
主对角线下的数据元素全部相同的矩阵为上三角矩阵(图 a),主对角线上元素全部相同的矩阵为下三角矩阵(图 4b)。
矩阵压缩的方式类似对称矩阵,不在此赘述了。重复元素c单独共享一个元素存储空间,其余的,将对称矩阵的下三角矩阵(或上三角矩阵)以行序为主序展开存在一维数组中,所以n维数组存储上下三角矩阵需要n(n+1)/2+1个元素空间
2.2.3 对角矩阵
[特点]在n阶的方阵中,所有非零元素都集中在以主对角线为中心的带状区域中,区域外的值全为0,则称为对角矩阵。常见的有三对角矩阵、五对角矩阵、七对角矩阵等。(数字代表对角矩阵的对角线数量)
按对角线来存储
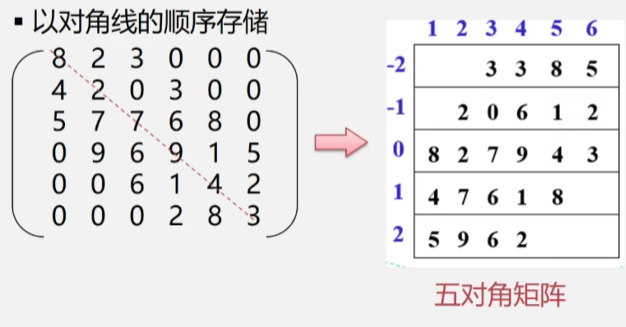
坐标对应关系:原矩阵a[i][j]映射到五对角矩阵中为a[j-i][j]。
2.2.4 稀疏矩阵
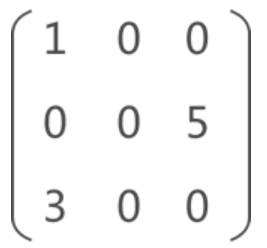
如果矩阵中分布有大量的元素 0,即非 0 元素非常少,这类矩阵称为稀疏矩阵。(当非零元素比所有元素小于等于0.05)
压缩存储稀疏矩阵的方法是:只存储矩阵中的非 0 元素,与前面的存储方法不同,稀疏矩阵非 0 元素的存储需同时存储该元素所在矩阵中的行标和列标。
2.2.4.1 三元组顺序表存储稀疏矩阵
用一个顺序表存储稀疏矩阵,顺组表的元素是一个三元组,分别记录非零元素的横坐标、纵坐标、和数值。为了矩阵的还原,通常会在顺序表表头加上矩阵信息,记录总行数、总列数、非零元素总个数。对于矩阵
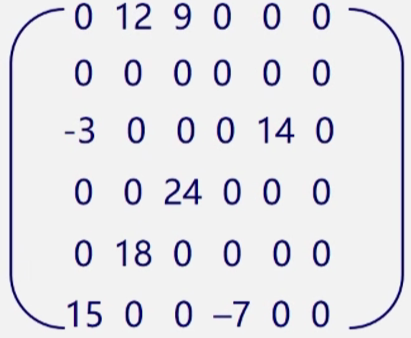
其三元顺序表为:
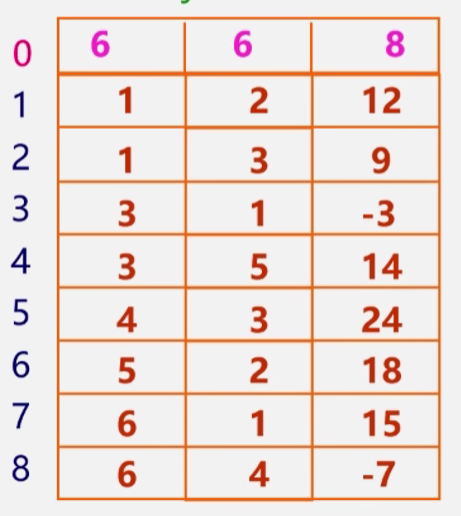
反过来我们也可以根据稀疏矩阵的三元顺序表得到系数矩阵
三元组顺序表优点:非零元在表中按行序有序存储,因此便于进行依行顺序处理的矩阵运算。
三元顺序表的缺点:不能随机存取,若按行号存取某一行的非零元则需从头开始进行查找。如三元顺序表因矩阵运算可能导致增加或减少零元素,三元组顺序表插入删除操作需要遍历或移动大量数据。
2.2.4.2 十字链表存储稀疏矩阵
十字链表中,矩阵非零元素用结点表示,节点存储矩阵位置及数值(row,col,value),此外还有right和down两个域
- right:用于链接同一行中的下一个非零元素;
- down:用以链接同一列中的下一个非零元素。
十字链表存储矩阵结点示意图
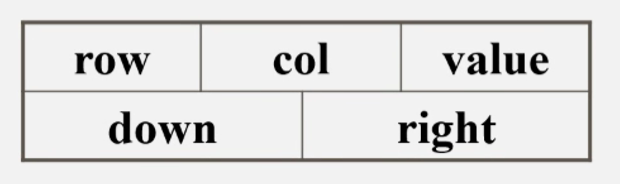
对于矩阵:
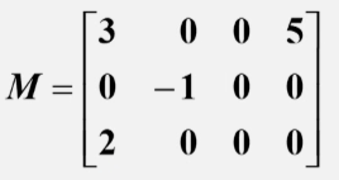
十字链表对应

十字链表会用到两数组:行数组和列数组。(方便随机存取,也能用链表)
行数组记录每一行第一个非零元素地址,列数组记录每一列第一个非零元素地址。
将非零元素封装在结点中,记录行坐标,列坐标,元素数值,当前行下一个非零元素,当前列下一个非零元素。
简述十字链表代码实现:先开辟好行数组和列数组,数组初值均为null。然后遍历稀疏矩阵,遇到非零元素就将非零元素封装在结点中(down和right初值均为零),封装好后就链接到行列数组中,若行列数组对应位置为null,则直接链接上;若行列数组非空就依次找到行列中相应的down和right域为空的位置,链接上,如此往复就能实现十字链表的存储。
下面是代码实现:
//用于存储非零元素的结点
typedef struct OLNode{
int i,j;//元素的行标和列标
int data;//元素的值
struct OLNode * right,*down;//两个指针域
//当前行写个非零元素,当前列下个非零元素
}OLNode, *OLink;
//表示十字链表的结构体:行列数组
typedef struct
{
OLink *rhead, *chead; //行和列链表头指针
int mu, nu, tu; //矩阵的行数,列数和非零元的个数
}CrossList;
//稀疏矩阵转化为十字链表
void CreateMatrix_OL(CrossList* M);
//输出十字链表
void display(CrossList M);
int main()
{
CrossList M;
M.rhead = NULL;
M.chead = NULL;
CreateMatrix_OL(&M);
printf("输出矩阵M:\n");
display(M);
return 0;
}
//稀疏矩阵转化为十字链表代码实现
void CreateMatrix_OL(CrossList* M)
{
int m, n, t;
int num = 0;
int i, j, e;
OLNode* p = NULL, * q = NULL;
printf("输入矩阵的行数、列数和非0元素个数:");
scanf("%d%d%d", &m, &n, &t);
(*M).mu = m;
(*M).nu = n;
(*M).tu = t;
if (!((*M).rhead = (OLink*)malloc((m + 1) * sizeof(OLink))) || !((*M).chead = (OLink*)malloc((n + 1) * sizeof(OLink))))
{
printf("初始化矩阵失败");
exit(0);
}
for (i = 0; i <= m; i++)
{
(*M).rhead[i] = NULL;
}
for (j = 0; j <= n; j++)
{
(*M).chead[j] = NULL;
}
while (num < t) {
scanf("%d%d%d", &i, &j, &e);
num++;
if (!(p = (OLNode*)malloc(sizeof(OLNode))))
{
printf("初始化三元组失败");
exit(0);
}
p->i = i;
p->j = j;
p->e = e;
//链接到行的指定位置
//如果第 i 行没有非 0 元素,或者第 i 行首个非 0 元素位于当前元素的右侧,直接将该元素放置到第 i 行的开头
if (NULL == (*M).rhead[i] || (*M).rhead[i]->j > j)
{
p->right = (*M).rhead[i];
(*M).rhead[i] = p;
}
else
{
//找到当前元素的位置
for (q = (*M).rhead[i]; (q->right) && q->right->j < j; q = q->right);
//将新非 0 元素插入 q 之后
p->right = q->right;
q->right = p;
}
//链接到列的指定位置
//如果第 j 列没有非 0 元素,或者第 j 列首个非 0 元素位于当前元素的下方,直接将该元素放置到第 j 列的开头
if (NULL == (*M).chead[j] || (*M).chead[j]->i > i)
{
p->down = (*M).chead[j];
(*M).chead[j] = p;
}
else
{
//找到当前元素要插入的位置
for (q = (*M).chead[j]; (q->down) && q->down->i < i; q = q->down);
//将当前元素插入到 q 指针下方
p->down = q->down;
q->down = p;
}
}
}
2.2.4.3 稀疏矩阵逆置
举证的转置,对于二维数组存储的矩阵,就是将a[i][j]换到a[j][i]的位置。很简单,但是对于稀疏矩阵,0元素很多,赋值没有什么意义,而且数组的存储有些浪费空间。所以我们讨论的是三元组法存储的稀疏矩阵
稀疏矩阵转置思路
- 将稀疏矩阵的行数和列数互换;
- 将三元组表(存储矩阵)中的 i 列和 j 列互换,实现矩阵的转置;
- 以 j 列为序,重新排列三元组表中存储各三元组的先后顺序;
三元组顺序表中,各个三元组会以行标做升序排序,行标相同的三元组以列标做升序排序。
#include<stdio.h>
#define NUM 10
//三元组
typedef struct {
int i, j;
int data;
}triple;
//三元组顺序表
typedef struct {
triple data[NUM];
int mu, nu, tu;
}TSMatrix;
//稀疏矩阵的转置
void transposeMatrix(TSMatrix M, TSMatrix* T) {
//1.稀疏矩阵的行数和列数互换
(*T).mu = M.nu;
(*T).nu = M.mu;
(*T).tu = M.tu;
if ((*T).tu) {
int col, p;
int q = 0;
//2.遍历原表中的各个三元组
for (col = 1; col <= M.nu; col++) {
//重复遍历原表 M.m 次,将所有三元组都存放到新表中
for (p = 0; p < M.tu; p++) {
//3.每次遍历,找到 j 列值最小的三元组,将它的行、列互换后存储到新表中
if (M.data[p].j == col) {
(*T).data[q].i = M.data[p].j;
(*T).data[q].j = M.data[p].i;
(*T).data[q].data = M.data[p].data;
//为存放下一个三元组做准备
q++;
}
}
}
}
}
int main() {
int i, k;
TSMatrix M, T;
M.mu = 3;
M.nu = 2;
M.tu = 4;
M.data[0].i = 1;
M.data[0].j = 2;
M.data[0].data = 1;
M.data[1].i = 2;
M.data[1].j = 2;
M.data[1].data = 3;
M.data[2].i = 3;
M.data[2].j = 1;
M.data[2].data = 6;
M.data[3].i = 3;
M.data[3].j = 2;
M.data[3].data = 5;
for (k = 0; k < NUM; k++) {
T.data[k].i = 0;
T.data[k].j = 0;
T.data[k].data = 0;
}
transposeMatrix(M, &T);
for (i = 0; i < T.tu; i++) {
printf("(%d,%d,%d)\n", T.data[i].i, T.data[i].j, T.data[i].data);
}
return 0;
}
3.广义表
3.1 广义表的概念及性质
广义表是线性表的推广,也称列表。
广义表记作:LS=(a1, … , an)
在线性表中ai只限于单个元素,广义表中ai可以是单个元素也可以是广义表。习惯上用大写字母表示广义表,小写字母表示原子。
广义表常见形式
- A = ():A 空表,长度为0
- B = (e):广义表 B 中只有一个原子 e,长度为1。
- C = (a,(b,c,d)) :广义表 C 中有两个元素,原子 a 和子表 (b,c,d),长度为2。
- D = (A,B,C):广义表 D 中存有 3 个子表,分别是A、B和C。这种表示方式等同于 D = ((),(e),(b,c,d)) 。
- E = (a,E):广义表 E 中有两个元素,原子 a 和它本身。这是一个递归广义表,等同于:E = (a,(a,(a,…)))。
- 注意,A = () 和 A = (()) 是不一样的。前者是空表,而后者是包含一个子表的广义表,只不过这个子表是空表。
具上推出重要结论:
-
广义表的元素可以是子表,子表的元素还可以是子表…所以广义表是一个多层次结构可以用图形象的表示,如:A = (),B = (e),C = (a,(b,c,d)) ,D = (A,B,C)
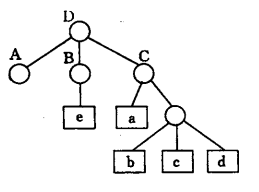
-
广义表可以为其他广义表所共享;如:广义表B共享表A,在B中不必列出A的值,而是通过名称来引用:B=(A)
-
广义表可以是一个递归的表,即广义表也可以是其本身的一个子表。如:E=(a,E)
广义表的表头和表尾:
当广义表不是空表时,称第一个数据(原子或子表)为"表头",剩下的数据构成子表则为"表尾"。所以非空广义表的表尾一定是一个广义表
广义表的性质:
-
广义表中的数据元素有相对次序:一个直接前驱和一个直接后继
-
广义表的长度:最外层所包含的数据元素的个数
如:C=(a,(b,c))是一个长度为2的广义表
-
广义表的深度:广义表完全展开后所包含括号的重数:
A = ()深度为1,B = (e)深度为1,C = (a,(b,c,d))深度为2,D = (A,B,C)深度为3
3.2 广义表的存储结构
广义表中的数据元素可以由不同的结构(或原子或列表),所以难以用顺序存储结构,通常用链式存储结构。常用的链式存储结构由两种,头尾链表的存储结构和扩展线性表的存储结构
3.2.1 头尾链表的存储结构
广义表中的数据元素可能为原子或列表,由此需要两种结构的结点:
- 一种是表结点,用以表示列表
- 一种是原子结点,用以表示原子。
前面说过,若列表不空,则可分解成表头和表尾。反之,一对确定的表头和表尾可惟一确定列表。
- 表结点可由3个域组成:标志域、指示表头的指针域和指示表尾的指针域
- 原子结点只需两个 域:标志域和值域(如图5.8所示)。其形式定义说明如下:
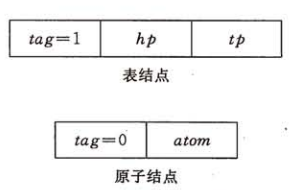
typedef struct GLNode {
int tag;//标志域区分原子结点还是表结点
union {
AtomType atom;//原子结点的值域,Atom是原子结点类型
struct {
struct Node* hp, * tp;
}ptr;//表结点的指针域,hp指向表头;tp指向表尾
};
}* Glist;
对应的A = (),B = (e),C = (a,(b,c,d)) ,D = (A,B,C),该广义表的存储结构如下:
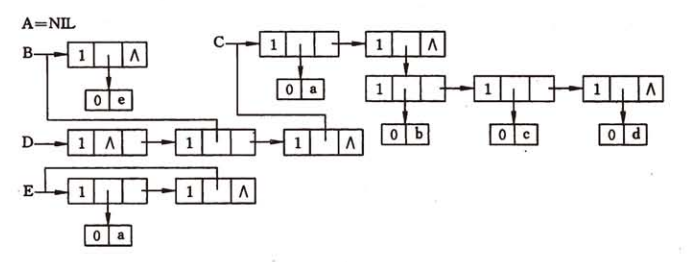
而具体代码实现则需要一个个手写,就不在此赘述了
头尾链表的存储结构有如下性质:
- 除空表的表头指针为空外,对任何非空列表,其表头指针均指向一个表结点,且该结点中的hp域指示列表表头(或为原子结点,或为表结点), tp域指向列表表尾(除非表尾为空,则指针为空,否则必为表结点)
- 容易分清列表中原子和子表所在层次。如在列表D中,原子a和e在同一层次上,而b、c和d在同一层次且比a和e低一层,B和C是同-层的子表
- 最高层的表结点个数即为列表的长度。
以上3个特点在某种程度上给列表的操作带来方便。也可采用另一种结点结构的链表表示列表
![[ 常用工具篇 ] 解决kali英文操作不方便的问题 -- kali 设置中文界面](https://img-blog.csdnimg.cn/a6669034d40146a0b8b4493c88384275.png)