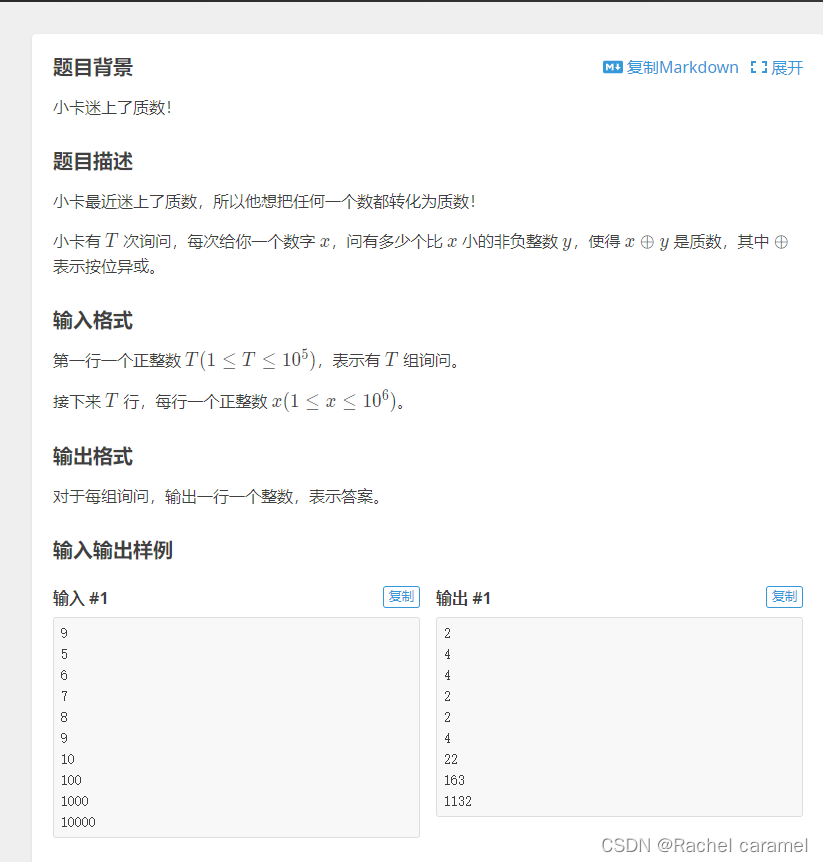
题目：

思路：
首先排除比较每一个比X小的数去看结果，因为一定会tle
然后考虑去和每一个比X小的数去看结果，去判定是否比它小，看起来是优秀了一些，但是 n以内的质数比例大约是$$\frac{1}{ln(n)}$$
不妨设x异或y=z，易得x异或z=y
逆向思维考虑x和什么样的质数z异或后得到的y会比x小，经过找规律可以发现
不妨设x的第i位为1，若x和y的前i-1位相同，这时第i位也相同，得到的数必然比x小（前i位相同，异或结果均得0），此时可以得出z的范围。
代码：

#include <bits/stdc++.h>
using namespace std;
const int maxn=2e6*+11;
int t,cnt,isprime[maxn],prime[maxn],sum[maxn];
void getprime()
{
	for(int i=1;i<=2e6;i++) isprime[i]=1;
	isprime[1]=0;
	for(int i=2;i<=2e6;i++)
	{
		if(isprime[i])
		{
			prime[++cnt]=i;
			if((long long)i*i<=2e6)
			{
				for(int j=i*i;j<=2e6;j+=i) isprime[j]=0;
			}
		}
	}
	//for(int i=1;i<=20;i++) cout<<prime[i]<<endl;
	for(int i=1;i<=2e6;i++)
	{
		sum[i]=sum[i-1];
		if(isprime[i]==1) sum[i]++;
	}
}
void handle(int x)
{
	int ans=0;
	for(int i=31;i>=0;i--) 
	{
		if((x>>i)&1)
		{
			int a=1<<i,b=(1<<(i+1))-1;
			ans+=sum[b]-sum[a-1];  
		}
		}
	printf("%d\n",ans);
}
int main()
{
	scanf("%d",&t);
	getprime();
	for(int i=1;i<=t;i++)
	{
		int x;
		scanf("%d",&x);
		handle(x);
	}
	return 0;
}