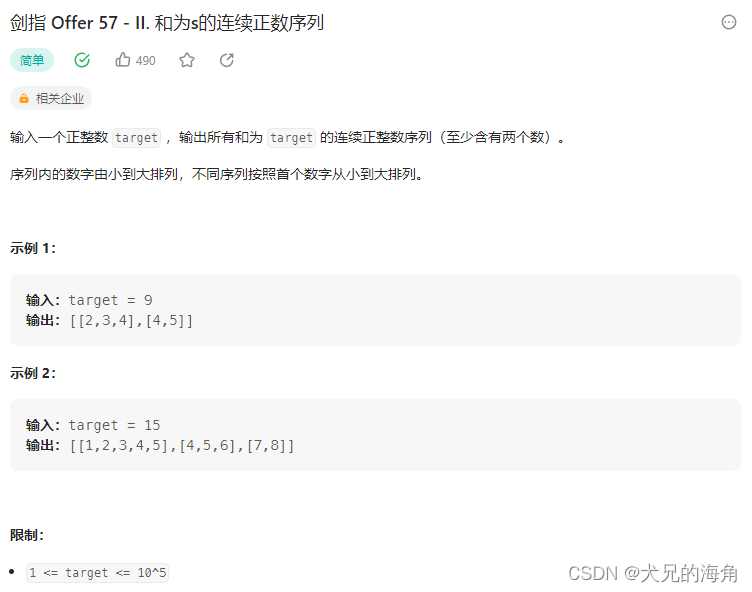
1、循环

我们可以一次循环每一个数，在 $\left \lfloor \frac{n}{2} \right \rfloor$ 的范围内循环检查添加新的数字后形成的数组和是否为target，若是则将当前数组加入结果当中；否则继续进行循环或跳出循环。

class Solution {
public:
    vector<vector<int>> findContinuousSequence(int target) {
        vector<vector<int>> vec;
        vector<int> res;
        int sum = 0, limit = (target - 1) / 2;
        for (int i = 1; i <= limit; ++i) {
            for (int j = i;; ++j) {
                sum += j;
                if (sum > target) {
                    sum = 0;
                    break;
                } else if (sum == target) {
                    res.clear();
                    for (int k = i; k <= j; ++k) {
                        res.emplace_back(k);
                    }
                    vec.emplace_back(res);
                    sum = 0;
                    break;
                }
            }
        }
        return vec;
    }
};

2、循环优化

我们可以利用求和公式对累加进行优化，在我们已经则是target的前提下，我们可以使用公式直接反向求得区间上限。因此我们只需要满足区间上限为整数即可。

class Solution {
public:
    vector<vector<int>> findContinuousSequence(int target) {
        vector<vector<int>> vec;
        vector<int> res;
        int sum = 0, limit = (target - 1) / 2;
        for (int x = 1; x <= limit; ++x) {
            long long delta = 1 - 4 * (x - 1ll * x * x - 2 * target);
            if (delta < 0) {
                continue;
            }
            int delta_sqrt = (int)sqrt(delta + 0.5);
            if (1ll * delta_sqrt * delta_sqrt == delta && (delta_sqrt - 1) % 2 == 0) {
                int y = (-1 + delta_sqrt) / 2;
                if (x < y) {
                    res.clear();
                    for (int i = x; i <= y; ++i) {
                        res.emplace_back(i);
                    }
                    vec.emplace_back(res);
                }
            }
        }
        return vec;
    }
};

3、双指针

我们可以使用左右指针来控制当前区间的范围：1、当 $s u m < t a r g e t$ 时，说明当前区间过小，我们需要右移右指针；2、当 $s u m = t a r g e t$ 时，说明当前区间就是我们需要的区间，将其加入结果当中并将左指针右移寻找下一个区间；3、当 $s u m > t a r g e t$ 时，说明当前区间超过范围，我们不需要继续查询，将左指针右移查找下一个可能的区间。循环在左指针超过总区间的一半时停止循环。

class Solution {
public:
    vector<vector<int>> findContinuousSequence(int target) {
        vector<vector<int>>vec;
        vector<int> res;
        for (int l = 1, r = 2; l < r;){
            int sum = (l + r) * (r - l + 1) / 2;
            if (sum == target) {
                res.clear();
                for (int i = l; i <= r; ++i) {
                    res.emplace_back(i);
                }
                vec.emplace_back(res);
                l++;
            } else if (sum < target) {
                r++;
            } else {
                l++;
            }
        }
        return vec;
    }
};