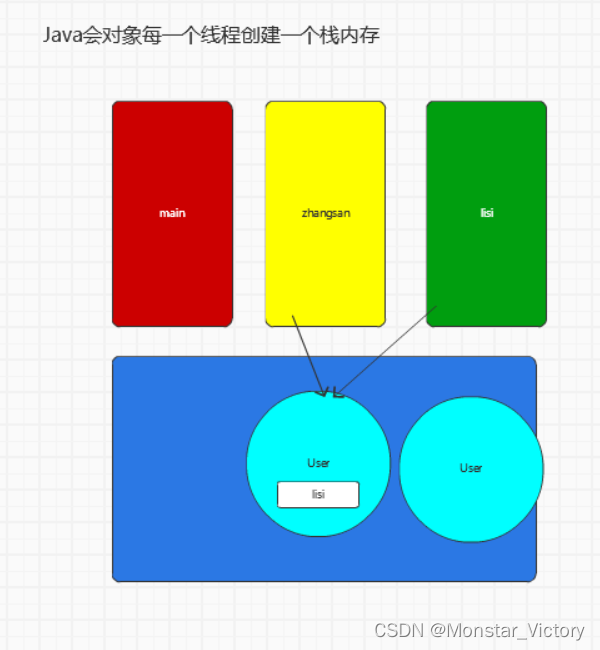
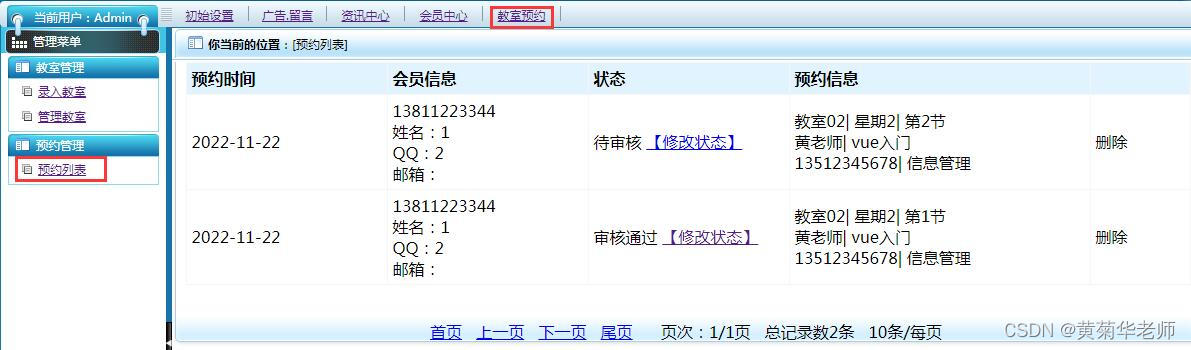
文章目录
- 一、Mahony算法的控制系统特征多项式
- 二、Kp, Ki参数调节方法
- 三、其他自适应调参法
我在之前的博客AHRS互补滤波(Mahony)算法及开源代码中曾提及Mahony算法的难点在于如何调节PI参数。
最近看到参考文献[1],提出了基于无阻尼自由频率设计设置Kp, Ki参数;以及严恭敏老师的文章Mahony航姿算法的参数调节方法,提出了基于时间常数或者无阻尼自由频率来设置Kp, Ki参数。这篇博客主要是对这两篇文章内容的整理与理解。
一、Mahony算法的控制系统特征多项式
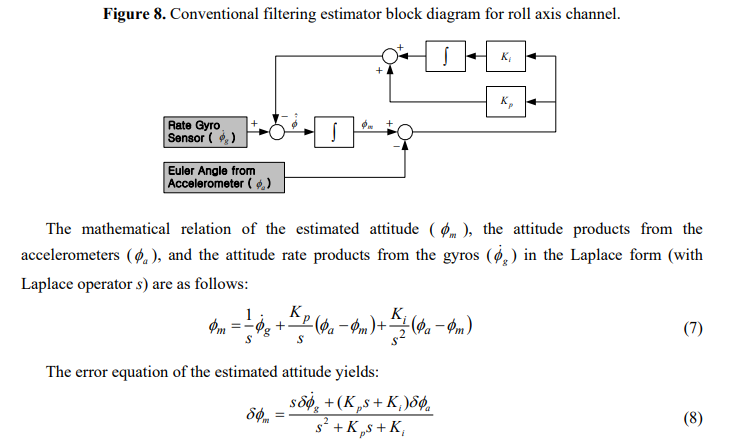
参考文献[1]中给出了Mahony算法的控制系统方程,如下图中公式(7)所示。把 ϕ m \phi{_m} ϕm整理出来就是它的传递函数,形式和公式(8)基本长一样,特征多项式为 s 2 + K p s + K i s^2+K_p{s}+K_i s2+Kps+Ki。这也是严老师“捷联惯导算法与组合导航原理-附录练习题”第49题的第一问的答案了,验证Mahony算法控制系统特征多项式为 s 2 + K p s + K i s^2+K_p{s}+K_i s2+Kps+Ki。
二、Kp, Ki参数调节方法
(1)文献1:
如下图所示,根据特征多项式,文献1认为当阻尼比为0.707时稳态响应最好,所以采用公式(10)和(11)来设置Kp和Ki,其实只需要设置一个参数,也就是无阻尼自由频率。

(2)严恭敏老师在文章中提及:

严老师所说的设置阻尼比的方法和文献1中的方法一致。关于为什么beta=2.146/tau,2.146的来源如下:


三、其他自适应调参法
在参考[3]中提到:
“关于这一块,现在研究的比较多就是如何实现自适应调参。固定的参数不能获得所有情况下的最优运动姿态角,可以设计参数可调的自适应算法在不同运动状态下进行调节参数的大小。其参数调节规则为:正常运动状态情况下,Kp和Ki值取为系统初始化值;当运动体具有较大运动加速度或姿态变化剧烈时,应选择较小的Kp值(可取其初始化值的0.1倍),而Ki值应在同一数量级内适当取大一点。具体取值需根据实际应用系统选取。”
参考文献
[1] Gain-Scheduled Complementary Filter Design for a MEMS Based Attitude and Heading Reference System
[2] Mahony航姿算法的参数调节方法
[3] 基于AHRS的三类姿态解算算法对比(含代码)-基于手机端惯性传感器的航迹推算算法(下)