一、字典树（trie）

引入

假设我们编写一个程序来实现一个词典，那么这个词典的所需要实现的两个功能就是插入和搜索。插入的话，我们最容易想到的就是创建一个字符指针数组，然后让这个数组去记录每一个单词的地址。但是当我们去搜索某个单词的时候，时间复杂度是O（N²），效率是非常低下的，因此为了优化这个问题，就出现了我们今天介绍的字典树。

1、什么是字典树？

我们在查字典的时候，先按照首字母去查，然后再去找剩下的字母。因此我们就知道字典树是一种搜索的算法，他是一种用来搜索的算法。

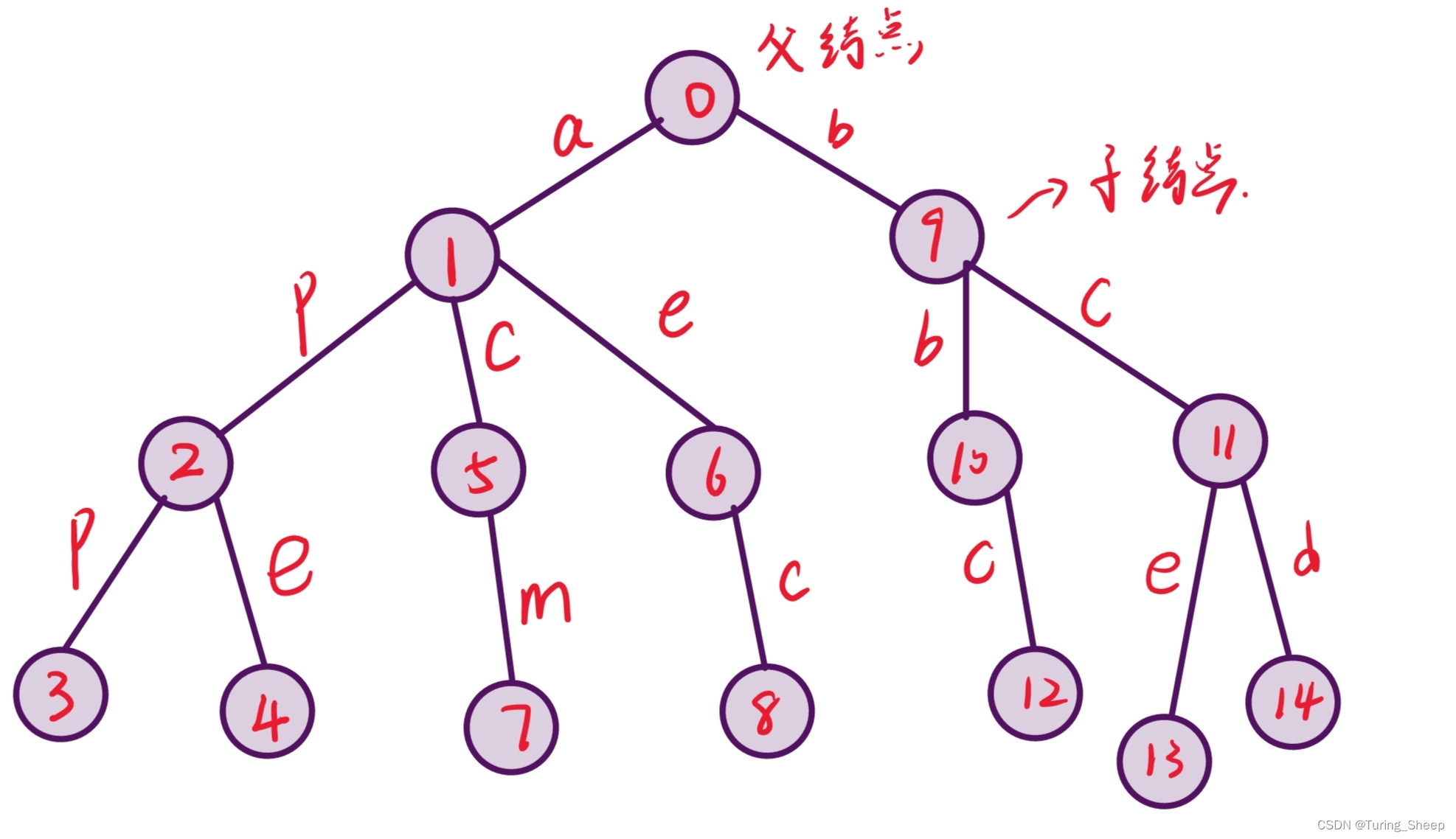
其逻辑结构如下图所示：

2、思路分析

我们继续看上面的图，这些图组成了一棵“树”（倒立的），这棵树又节点和边组成。那么我们的字符串中的字符就记录在这些边中，也就是说，我们从父节点0出发，沿着一条名字为“a”的边找到了节点1，然后再从节点1出发沿着一条名字为“p”的边找到了第二个节点，以此类推…假设我们想要查找一个字符串，其实本质上就是给出了一条路，按照这条路上的各个边，我们都能找到节点，那就说明这个字符串是存在的。假设我们按照字符串所指出的路，去找节点，我们发现沿着这条路中的边去走的时候，找不到节点了，那就说明这个字符串是不存在的。

3、复杂度分析

我们利用这个搜索算法主要执行两种操作：一种是完善我们的字典，即插入字符串，另外一种是去搜索。

插入操作：其实就是一个搭建节点的过程，时间复杂度是O（N）

搜索操作：搜索的时间复杂度是O（N）

4、模板

（1）问题：

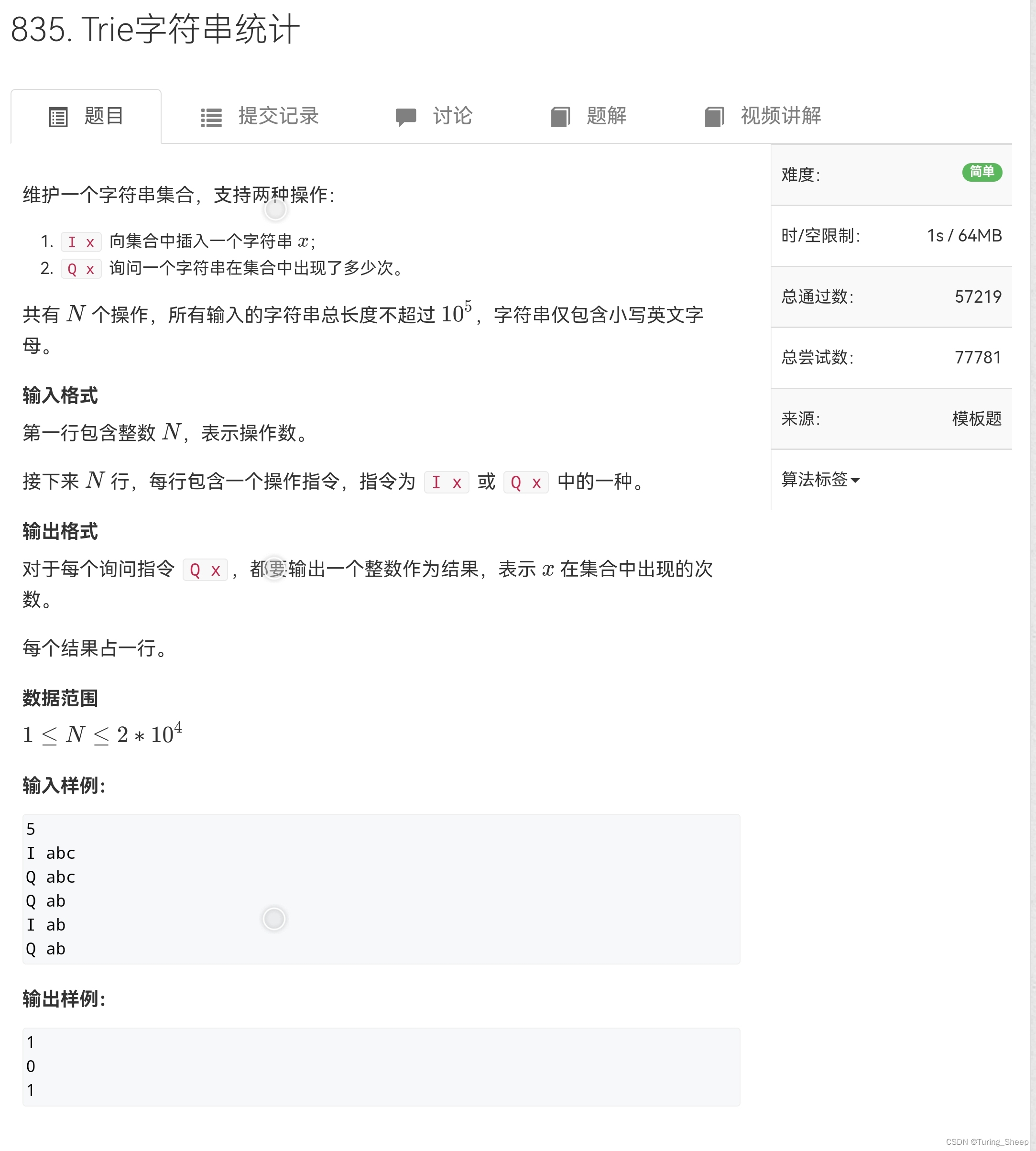
（2）模板：

#include<iostream>
using namespace std;
const int N=200010;
char str[100010];
int cnt[N],son[N][26],idx;
void insert(char*str)
{
    int p=0;
    for(int i=0;str[i];i++)
    {
        int u=str[i]-'a';
        if(!son[p][u])son[p][u]=++idx;
        p=son[p][u];
    }
    cnt[p]++;
}
int quary(char*str)
{
    int p=0;
    for(int i=0;str[i];i++)
    {
        int u=str[i]-'a';
        if(!son[p][u])return 0;
        p=son[p][u];
    }
    return cnt[p];
}

int main()
{
    int n;
    cin>>n;

    while(n--)
    {
        char op;
        cin>>op>>str;
        if(op=='I')
        {
            insert(str);
        }
        else
        {
            printf("%d\n",quary(str));
        }
    }
    return 0;
}

（3）模板代码解释：

变量解释：

son[x][r]=y：这个变量的意思是我们通过当前的节点x，沿着r这条路线到达节点y。
借此我们就能够理解son[N][26]，节点个数的最大值是N，由于我们的路线是通过26个字母来说明的，所以从当前节点到下一个节点之间最多有26条路线。

idx : idx是给用来给节点编号的，因为我们每一个节点是不同的，所以我们通过++idx来给每次创建的子节点来编号。

cnt[p]：这里的p指的是我们当前的节点，当我们有一个单词在p节点处结束的时候，我们就在这里做一个标记，为什么要这么做呢？假设我们存储一个单词：apple,但是我们查询的是app，app仅仅是apple的一个前缀，但是在字典树中并不存在这个单词，仅仅是存在app这条路。因此，我们需要走到这条路的末尾的时候，通过cnt[p]来判断一下，是否真的存在这个单词。简单的来说，idx就是来给每个单词的末尾打上一个标记。

插入函数解释：

我们先把字母转化成0到25的整形数据。
接着我们从根节点出发，通过单词的路线去寻找节点，如果不存在我们就创建一个子节点，然后通过idx给新的节点编号。最后在这个单词末尾节点处，通过cnt来打上标记。

搜索函数解释：

一个单词存在，必须满足两个条件，按照单词的路线，能够找到每一个节点。并切在末尾节点处存在标记。

我们先利用所查单词去寻找节点，如果一个节点不存在，即：son[p][u]==0，说明这里没有节点，那么这个单词必定是不存在的。假设按照单词所说的路线去寻找，我们能够找到每个节点，我们在通过cnt[p]判断一下，这个单词是真的存在，还是说这个单词仅仅是其他单词的前缀。

二、并查集（找祖宗算法）

1、什么是并查集

并查集是一个树形的数据结构，那么其作用其实就是并和查。并的意思就是合并两个树，查的意思就是判断某个节点否属于这棵树。

2、思路分析

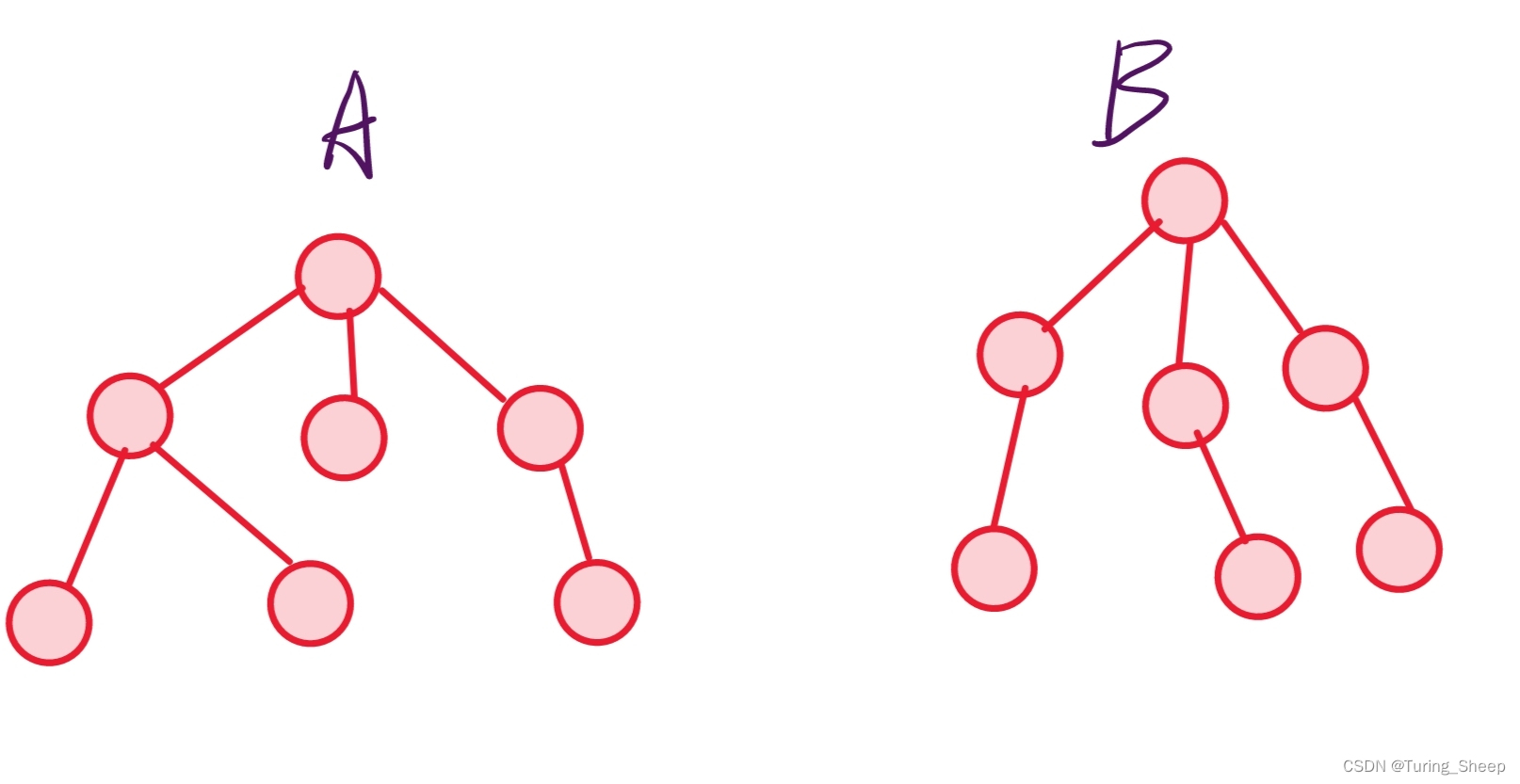
其实就类似于家族的概念，合并就是将两个家族合并，我们只需要将让B家族的祖宗认A家族的祖宗为祖宗，那么A和B家族就都属于A家族了。

假设我们想判断一个人是否属于这个家族，我们可以去查这个人的祖宗是不是这个家族的创始人，即可判断。

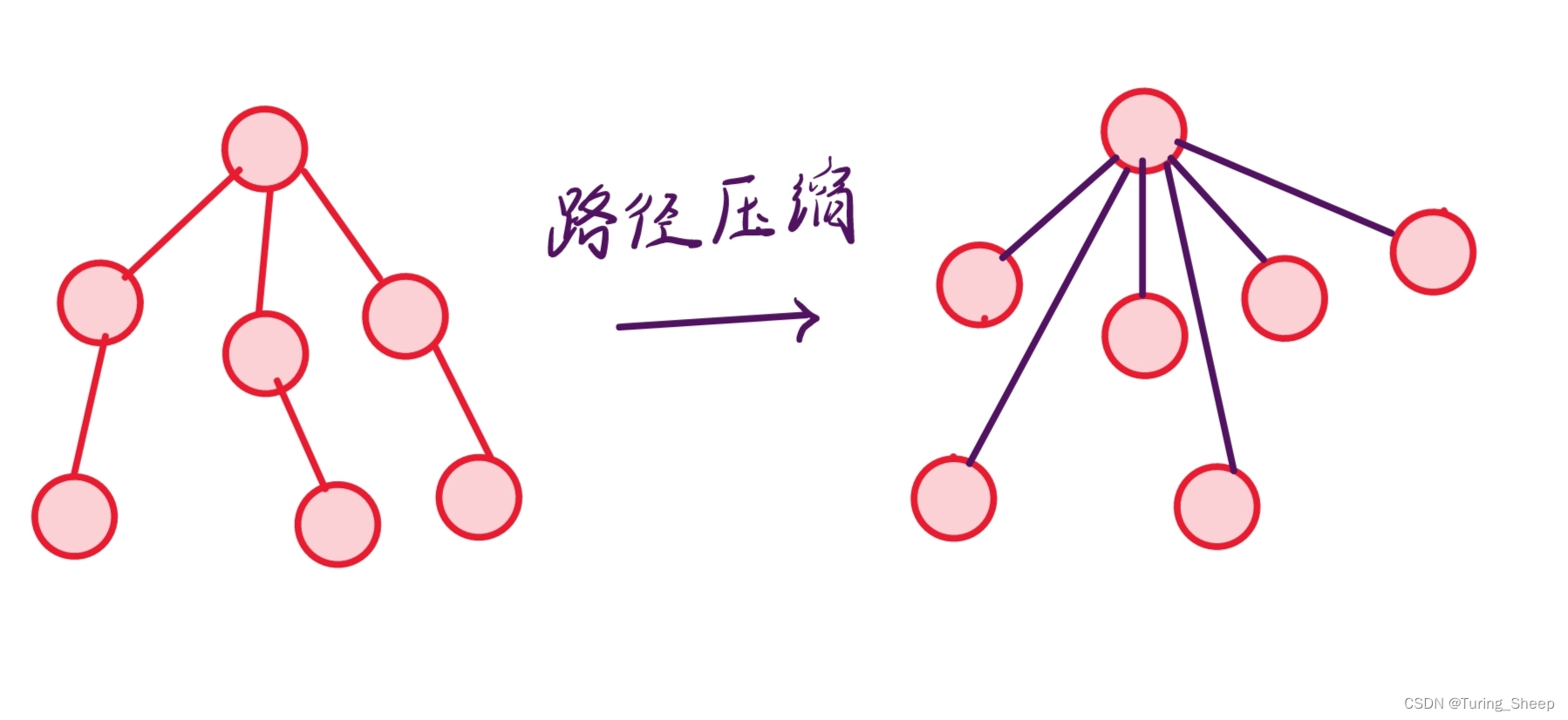
3、算法优化——路径压缩

当我们想判断一个子节点是否属于该树的时候，我们需要去找他的祖宗，随着树的层数越多，我们需要回溯的次数也就越多。因此，为了高效地判断，我们可以在找找到一个数的祖宗后，直接将其父节点该成祖宗节点，这样我们的查找算法的时间复杂度就近似于O（1）

4、模板

（1）问题：

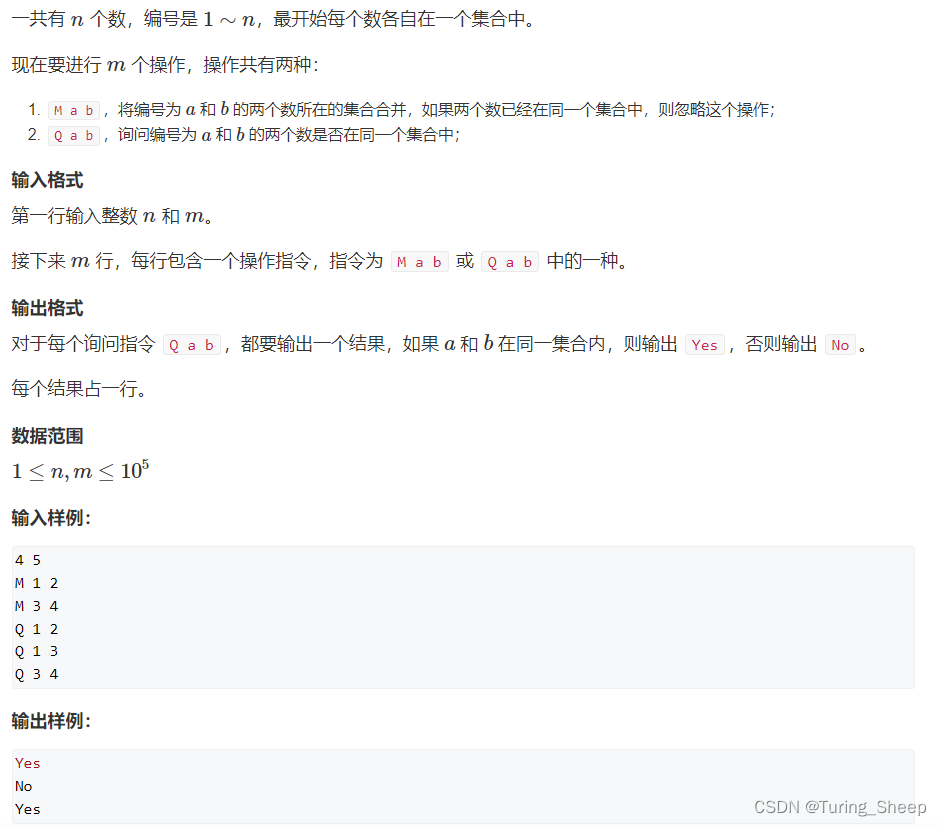
（2）模板：

#include<iostream>
using namespace std;
const int N=1e5+10;
int p[N];

int find(int x)
{
    if(p[x]!=x)return p[x]=find(p[x]);
    return p[x];
}

int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)p[i]=i;
    while(m--)
    {
        char op[2];
        int x,y;
        scanf("%s%d%d",op,&x,&y);
        if(op[0]=='M')
        {
            p[find(x)]=find(y);
        }
        else
        {
            if(find(x)==find(y))puts("Yes");
            else puts("No");
        }
    }
    return 0;
}

（3）模板解释：

变量解释：

int p[N] ：我们假设写一个p[1]=2，这一行代码的意思就是，节点1的父节点是2。那么祖宗节点怎么办呢？我们可以将祖宗节点的父节点设置为自身。即p[x]=x，这也是我们对所有节点初始化的操作。

find函数解释：

find函数是用来找祖宗用的。我们采用了一个递归的写法。同时，我们再递归的同时还写了这样一行语句：p(x)=find(x)，就是将x的父节点设置为祖宗。这样的话就完成了路径压缩的优化。