【机器学习】SVM入门-硬间隔模型

news2024/10/7 18:31:05

本站原创文章，转载请说明来自《老饼讲解-机器学习》ml.bbbdata.com

一. SVM的目标和思想

1.1 SVM硬间隔模型的原始目的

1.2 SVM的直接目标

1.3 什么是支持向量

二. SVM的支持平面的表示方式

2.1 支持面表示方式的初步思路

2.2 初步思路的缺陷与改进

2.3 支持面的最终表示方式

三. SVM模型表达式

3.1 SVM模型表达式

3.2 wx+b的意义

四. SVM模型损失函数

4.1 损失函数

4.2 损失函数解说

本文解说SVM的硬间隔损失函数的定义和思想，以及硬间隔损失函数的推导

一. SVM的目标和思想

本节先大概了解SVM模型的主要思想和目标

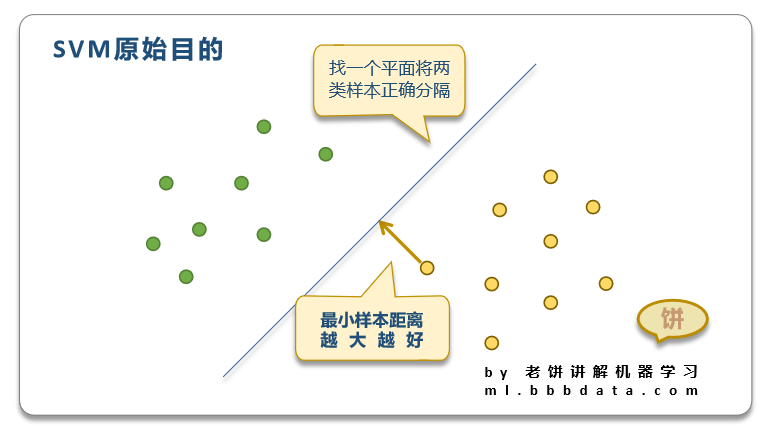
1.1 SVM硬间隔模型的原始目的

SVM硬间隔模型用于样本线性可分的二分类，

它的原始目的是找出一个判别面，让样本离判断面的最小距离最大化，

这样的判别面称为SVM的最优判别面

声明
本文所说的SVM都是指硬间隔模型，它基于样本线性可分，
硬间隔是相对软间隔模型而言，软间隔不要求样本线性可分

1.2 SVM的直接目标

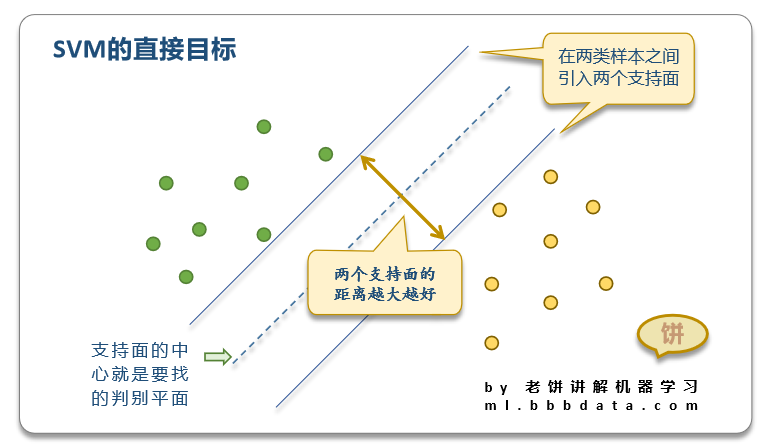
直接找最优判别面较难找，SVM并不是直接找最优判别面，
而是在两类样本之间，引入两个平行的支持面(支持面之间不能有样本)
然后让支持平面尽量撑开，

当两个支持平面的距离最大化时，
两个支持平面的中心，就是要找的最优判别面
所以，
SVM的直接目标是找出距离最大化的两个支持面
从而曲线救国达到找出最优判别面的原始目的

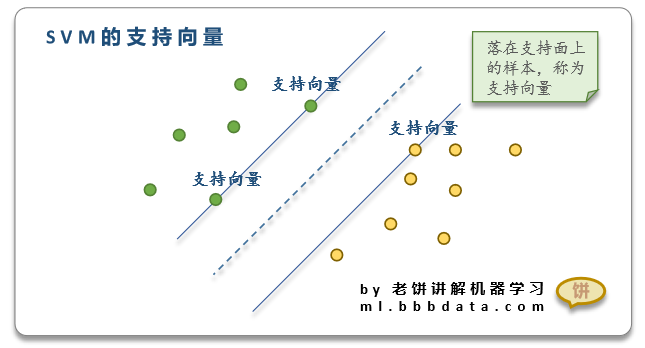
1.3 什么是支持向量

落在支持面上的样本，称为支持向量，
它们是模型的关键样本

也就是说，看起来用很多样本训练模型，但最关键的样本其实并不多

二. SVM的支持平面的表示方式

本节说明SVM支持平面的表示方法，是后面讲述模型和损失函数的基础和前提

2.1 支持面表示方式的初步思路

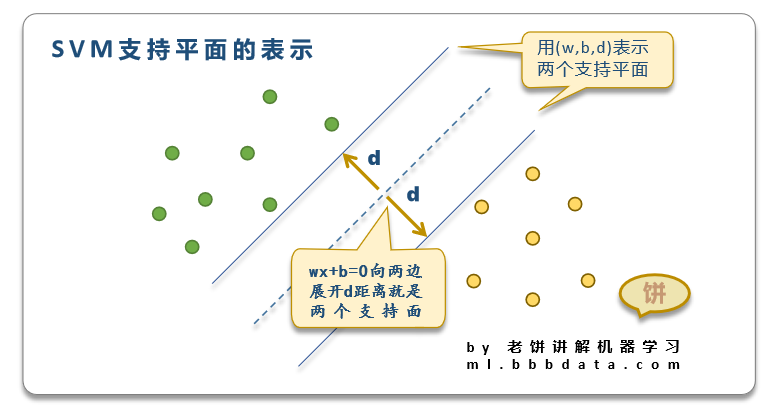
一组支持面可以由(w,b,d)指定，

（w,b)代表两个支持面的中心平面wx+b =0，
中心平面向两边展开d距离，就是两个支持面
注： wx+b =0 同时也就是判别面

2.2 初步思路的缺陷与改进

初步思路中的缺陷
初步思路中，用(w,b,d)来表示支持面
这种表述最大的问题是，
由于wx+b=0与k(wx+b)=0表示的是同一个平面，
虽然最优支持面只有一组，假设为(w,b,d)
但对所有k>0, (kw,kb,d)都能表示这组最优支持平面，
即最后的解(的表述)存在无限多个

改进思路
注意到d的取值范围为 $(0,+\infty )$
对平面wx+b=0， $\dfrac{1}{\left \| w \right \| }$ 的取值范围也是 $(0,+\infty )$ ，

不妨用 $\dfrac{1}{\left \| w \right \| }$ 来替代d,这样可以消去d，
这样的表示能让解的表述较为唯一，
如下

（w,b）表示的是以Wx+b=0为中心面两边展开 $\dfrac{1}{\left \| w \right \| }$ 距离的一组支持面

而（kw,kb）虽然与(W,b)的中心面一致，但撑开的距离为 $\dfrac{1}{\left \| kw \right \| }$ ,
所以两者表示的不是同一组支持面（k=-1除外）

2.3 支持面的最终表示方式

SVM对支持面的表示最终设计如下，
👉支持面的表示方法：(w,b)
其中，
wx+b=0是两个支持面的中心
$d=\dfrac{1}{\left \| w \right \| }$
是支持面离中面心的距离
即由wx+b=0两边展开 $\dfrac{1}{\left \| w \right \| }$
距离，就得到了两个支持面

注：同时，wx+b=0也就是最后需要得到的判别面

三. SVM模型表达式

本节展示SVM模型的表达式，和讲解模型表达式的意义

3.1 SVM模型表达式

SVM模型数学表达式为
$\text{y} = \text{sign}(wx+b)$
也就是判断样本是在判别面的正侧还是负侧，
从而决定模型是正样本还是负样本

特别说明

光看表达式很容易让人误解，以为SVM是一个平面的模型
但其实它是一个“三个平面”的模型：
以wx+b=0为判别平面， $\dfrac{1}{\left \| w \right \|}$ 为支持距离生成两个支持平面，

共三个平面，如图：

这家伙是带翅膀的！

虽然最后的判断核心是依靠判别面，

但支持面提供了样本可信程度的一个参考

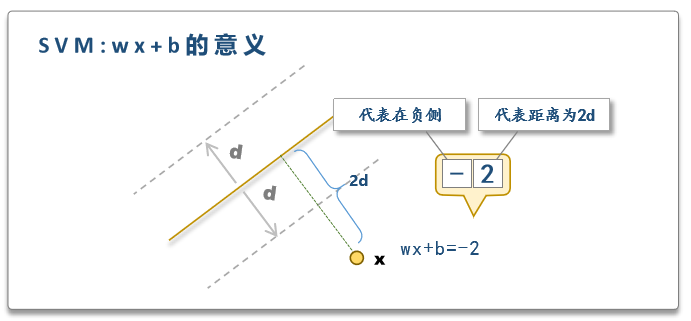
3.2 wx+b的意义

由几何关系可知，样本到判别面的距离为
$d(x) = \left | \dfrac{wx+b}{\left \| w \right \| } \right |$

如果保留距离的正负号，则有
$d_{\pm }(x) = \dfrac{wx_i+b}{\left \| w \right \| }$

即有：
$\begin{aligned} &d_{\pm }(x) = \dfrac{wx+b}{\left \| w \right \| } \\ \Rightarrow &d_{\pm }(x) = d*(wx+b) \\ \Rightarrow & \dfrac{ d_{\pm }(x)}{d} = wx+b \end{aligned}$

其中 $d=\dfrac{1}{\left \| w \right \| }$ 是支持平面到判别平面的距离，
所以，wx+b的意义，是带符号的样本距离与支持距离的比值，
这样比较绕，不妨如下理解：

wx+b就是样本与判别平面的距离，
但这个距离是带正负号的，且它以支持距离为单位

四. SVM模型损失函数

本节讲解SVM模型(硬间隔)的损失函数和解读损失函数的意义

4.1 损失函数

SVM硬间隔损失函数如下

损失函数
$L(w,b) = \dfrac{1}{2} \left \| w \right \|^2$
约束条件：
$\text{y}_i\left ( w x_i +b\right ) -1\geqslant 0$

4.2 损失函数解说

损失函数的优化目标
损失函数的优化目标 $L(w,b) = \dfrac{1}{2} \left \| w \right \|^2$ 的本质是最小化 $\left \| w \right \|$ ，
又 $\left \| w \right \|=\dfrac{1}{d}$ ，所以本质是最大化两个支持面平间的距离(2d)
将 $\left \| w \right \|$ 改成 $\dfrac{1}{2} \left \| w \right \|^2$ ，
加平方是为了可以去掉2范数里的根号，同时乘以 $\dfrac{1}{2}$ ，
进一步方便损失函数求导后的简洁

损失函数的约束条件
下面我们分析约束条件 $\text{y}_i\left ( w x_i +b\right ) \geqslant 1$ ，
将它拆成 $\text{y}_i=1$ 和 $\text{y}_i=-1$ 两种场景：
$\begin{cases} w x_i +b \geqslant 1, & \text{y}_i=+1 \\ w x_i +b \leqslant -1, & \text{y}_i=-1 \end{cases}$

上面已经分析过，
wx+b 的意义就是样本与判别平面的距离(带符号，以支持距离为单位)，
所以约束条件就是，
y=+1 时，即正样本，不能在正支持面的负侧
y= -1时，即负样本，不能在负支持面的正侧

损失函数意义总结
损失函数总的意思，
就是约束两个支持面必须在正负样本之间，
且两个支持面之间不能有样本，
然后最大化两个支持面之间的距离

笔者小故事

辨析清楚判别面、支持面、支持向量这些概念非常重要，
笔者最初学习时，因为不清晰这些概念，常常被误导
例如，
笔者误以为SVM要搞的是判别面，
在理解算法时，所有符号都往判别面上挂，
特别是损失函数中的 $\dfrac{1}{2} \left \| w \right \|^2$ ，百思不得其解，
其实SVM一切一切一切都是在搞支持面，
符号的含义、函数的目标等等，都应该往支持面上挂。
损失函数 $\dfrac{1}{2} \left \| w \right \|^2$ 中的w在这里就不应理解成判别面的权重
而是支持面之间的距离,这才是它在损失函数中所要代表的对象
又例如，
笔者以为支持向量构成了支持面，
在看到支持面上只有一个样本时就疑惑了，
一个样本怎么能构成面呢？
其实不然，支持向量只是一个定义，说明这些样本是关键样本
SVM一直在找的只有支持面，支持向量和判别面是顺带出来的东西
认识到这点对笔者来说非常重要，
对SVM的理解方向正确了，一切也就简单合理了~