文章目录
- 红黑树
- 性质
- 红黑树的插入
- 前言
- 寻找插入位置
- 情况 1.0
- 情况 1.1
- 情况 1.2
- 情况 1.3
- 情况 2.0
- 情况 2.1
- 情况 2.2
- 情况 2.3
- 完整代码
- 红黑树的检验
- 验证代码和用例
红黑树
上篇文章我们说到 AVL 树在新增 / 减少结点的时候会进行旋转以保持 AVL 树的高度平衡, 但是实际上在需要 频繁加入 / 删除结点的场景中, AVL 树在旋转上开销会很大, 总体效率也会较为低下。
故而有这样一个数据结构——红黑树, 这里我们不再讨论平衡因子, 而是维护结点中的颜色（只有红或黑）来间接地调整树的「相对平衡」，也就是说红黑树的平衡并没有 AVL 树那样严格，所以相比 AVL 树，红黑树有的旋转次数会显著减少，我们来具体看看：
性质
如果一棵树是红黑树，它必然有如下性质：（这几条性质建议多熟悉一下）
- 结点只有红，黑两种属性（显而易见对吧，红黑树嘛）
- 根节点为黑色
- 叶子结点视为黑色，这里的叶子结点指的是最底层的空节点
- 不能存在两个连续的红色节点
- 从「任意节点开始到其后代叶子节点」的简单路径上，有「相同数量的黑色节点」
具备了以上几条性质，我们就能保证：红黑树最长路径是最短路径的两倍
因为在「从任意结点开始到叶子结点具有相同数量的黑色结点」和「不能连续存在两个红色结点」的限制，最短路径就是路径上 N 个点全是 黑色的，最长路径就是这 N 个黑色结点和 N 个红色结点交替出现，长度最多是2 N，故而具备了这个特点。
然后对于红黑树的节点，我们定义为：
private static class RBTreeNode {
private RBTreeNode parent;
private RBTreeNode left;
private RBTreeNode right;
private COLOR color; // 结点颜色
int val ;
}
// 在另一个 Java 文件中
public enum COLOR {
BLACK, RED
}
红黑树的插入
前言
首先对于一个新节点的插入，这个新节点我们需要先默认设置为红色，那为什么不设置成黑色呢？
- 在插入新节点之前，这棵树肯定已经是红黑树了，那么它就满足性质4（任意结点节点到叶子结点路径上黑色节点个数相等），而如果这时候插入一个黑色的节点，那肯定会破坏这个性质。
- 而我们设定新节点为红色的，那只是可能会破坏性质3（不存在连续两红），但是我们可以通过修改结点颜色或者树的结构来纠正这棵红黑树
寻找插入位置
接下来开始我们的红黑树插入阶段：
如果红黑树的根节点为空，那么这个新节点设置为根节点即可，再将这个点的颜色设为黑色（因为新节点默认是红色, 且根节点为黑）
否则：
我们就要寻找新节点的插入位置了，这和 AVL 树对应的代码是一样的（二分，然后连接新节点），这里直接上代码
public boolean insert(int val) {
RBTreeNode newNode = new RBTreeNode(val);
if (root == null) {
root = newNode;
root.color = BLACK; // 根节点颜色为 黑
return true;
}
// 寻找插入位置
RBTreeNode parent = null;
RBTreeNode cur = root;
while (cur != null) {
if (cur.val < val) {
parent = cur;
cur = cur.right;
} else if (cur.val > val) {
parent = cur;
cur = cur.left;
} else {
return true; // 重复节点
}
}
// 至此 cur 为空，parent 为 cur 的父节点
// 完成节点的插入
if (parent.val > val) {
parent.left = newNode;
} else {
parent.right = newNode;
}
newNode.parent = parent; // 双向连接
}
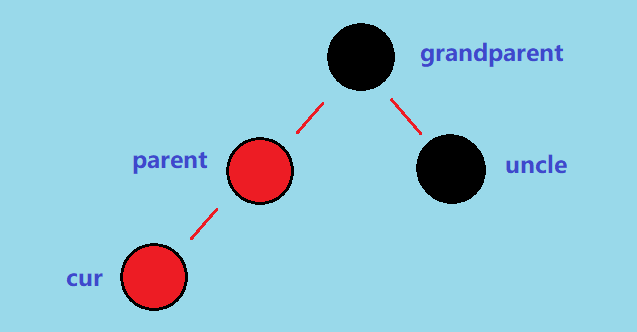
接着，我们来熟悉一下这几个结点 👇，接下来需要频繁用到
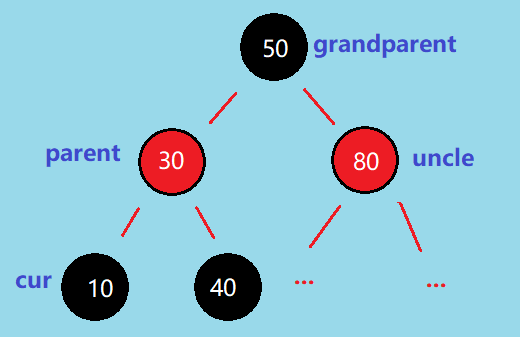
因为插入新元素之前树就是红黑树了，而我们新插入的结点（下文简称为 newNode）都是默认红色的，所以当 newNode 的 parent 是黑色的时候，这时候是不会破坏红黑树的性质的，直接插入即可。
所以只有当 cur.parent 的颜色为红色的时候 ，我们需要从 cur 结点开始往根节点「检查并调整树的颜色或者结构」，于是就有这样的 while 循环
while (parent != null && parent.color == RED)
然后由于接下来的情况需要基于 grandparent 而定，所以我们再随手定义一个 祖父结点
RBTreeNode grandparent = parent.parent
（需要注意：只有 parent.color = RED 的时候，才会进入循环，而又因为根节点是黑色的，所以 parent 不可能为根节点，因而进入循环后，祖父结点必然存在不为空）
情况 1.0
第一大情况，如下，也就是 parent 是「左树」
if (parent == grandparent.left)
然后基于这个条件下，还需要定义叔叔结点
RBTreeNode uncle = grandparent.right;
然后就有了以下三种情况
情况 1.1
if (uncle != null && uncle.color = RED)
也就是这种情况：
原树是棵红黑树，现在插入了一个新节点，以至于连续出现两个红结点，而我们如果改变 cur 的颜色也是行不通的，这样的话从 parent 通向叶子节点的黑色结点数就不相等了。
所以首先我们需要将 parent 和 uncle 改成黑色
parent.color = BLACK; uncle.color = BLACK;，这样就满足红黑树的性质了。如下：
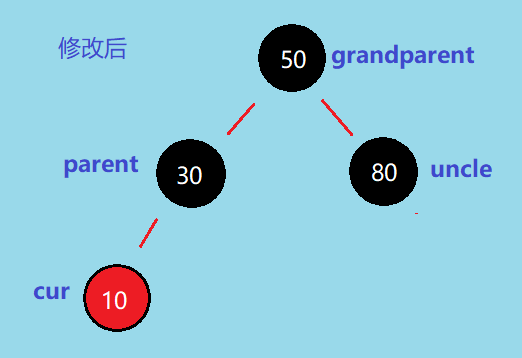
但是 grandparent 有可能是有父亲结点的，并且父亲结点可能是红，也可能是黑
首先，如果 grandparent.parent 是黑色，那么各路径的黑色结点数就不相等了，如下图
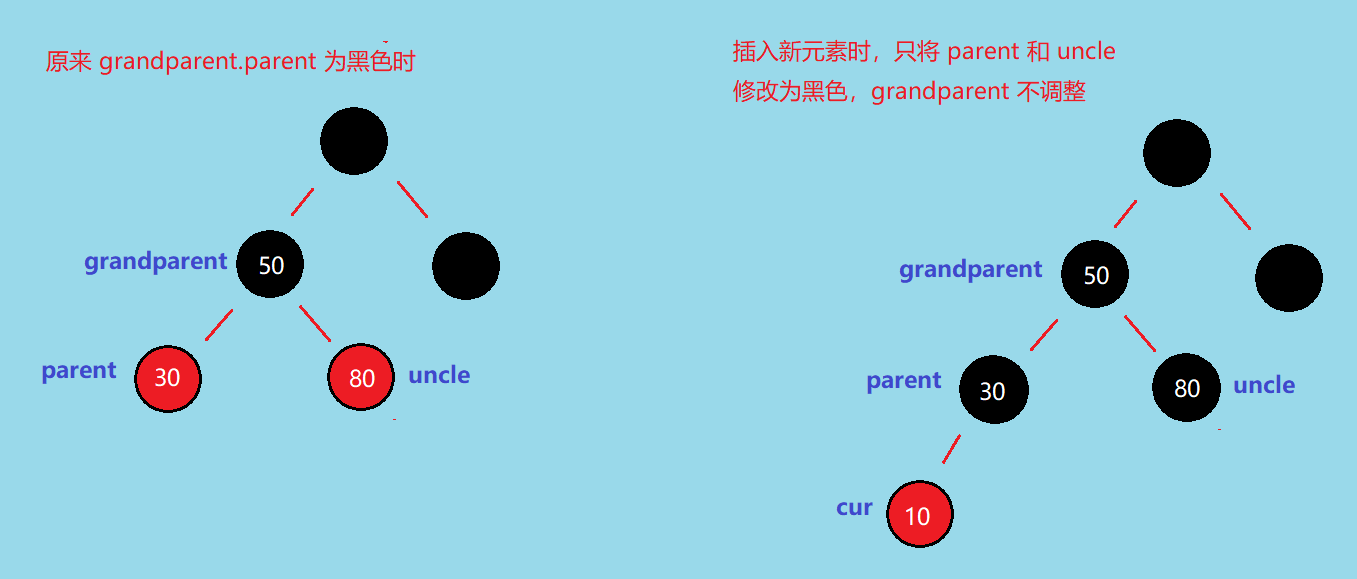
这时候如果我们将 grandparent 改成红色，那可以解决这种情况
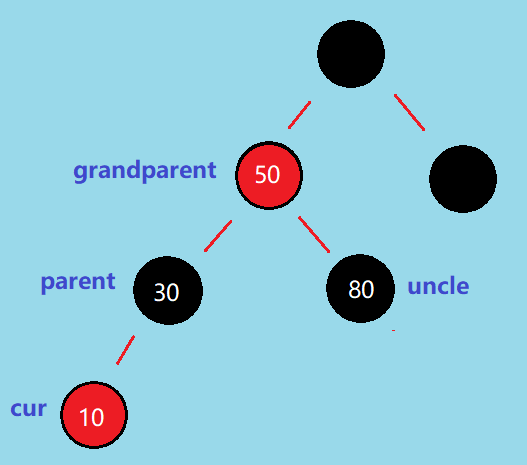
而 如果 grandparent.parent 是红色的，只将 parent 和 uncle 改成黑色还是会出现「路径黑色个数不等」的情况
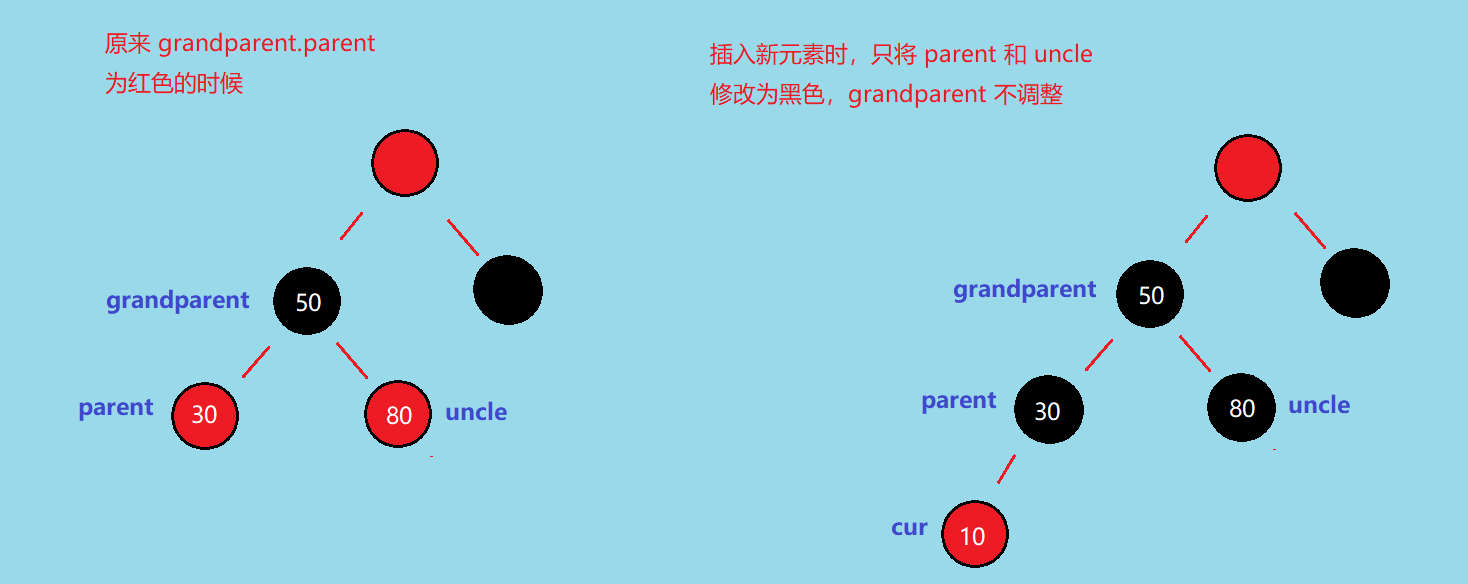
将 grandparent 改成红色，也会出现「连续两红」的问题，如下
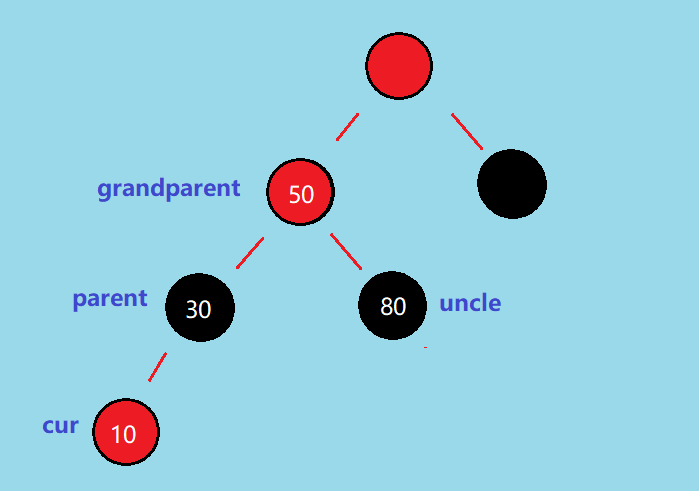
因此，正确的做法是：将 parent 和 uncle 改成黑色，grandparent 直接改成红色, 等到插入操作即将结束时再将 root 改为黑色
如下图，我们将 parent 和 uncle 改成黑色，再将 grandparent 改成红色，但是有可能grandparent上面的结点也都还需要调整，我们我们要重新调整 cur 的指向，让 cur = grandparent，于是当轮调整结束，再进入一次 while 循环，但是这次 parent 不为红色了，于是退出 while，调整结束，但是由于刚刚将 grandparent 改成了红色（也就是下图中根节点被我们改成了红色），所以我们在调整过程结束时再让 root 变成黑色。
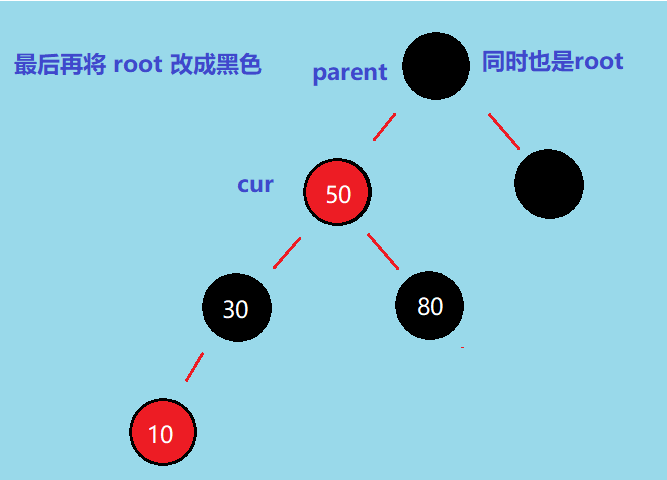
情况 1.1执行完后，别忘了 有可能上面的结点也需要进行调整，所以我们也需要更新 cur 和 parent 的位置：
cur = grandparent;
parent = cur.parent;
综上所述情况 1.1 代码如下
if (uncle != null && uncle.color == RED) {
parent.color = BLACK;
uncle.color = BLACK;
grandparent.color = RED; // 修改颜色
cur = grandparent; // 调整 cur 引用位置
parent = cur.parent;
// grandparent 先统一改红，调整结束再做处理
}
情况 1.2
1.1 的情况是 uncle 存在且为红色，那么剩下的情况就是 uncle 不存在，或 uncle 为黑色
并且 cur 为 parent 的左孩子（这个条件暂时不用太关注，后面会讲到）
进入 else 语句， 也就是(uncle == null || uncle.color == BLACK)
这种情况下普通的直接插入是无法达成这种状态的，这种状态只会出现在调整的过程中，因为 uncle 为黑色，为了保证黑色结点数量，parent 也得是黑色的结点(因为新插入的 cur 为红色)，而 parent 硬要是红色的话那么这棵树也就不是红黑树了
我们拿这个图举一个👇需要进行情况 1.2 进行调整的例子，针对下图：现在我们插入了 cur 这个新节点
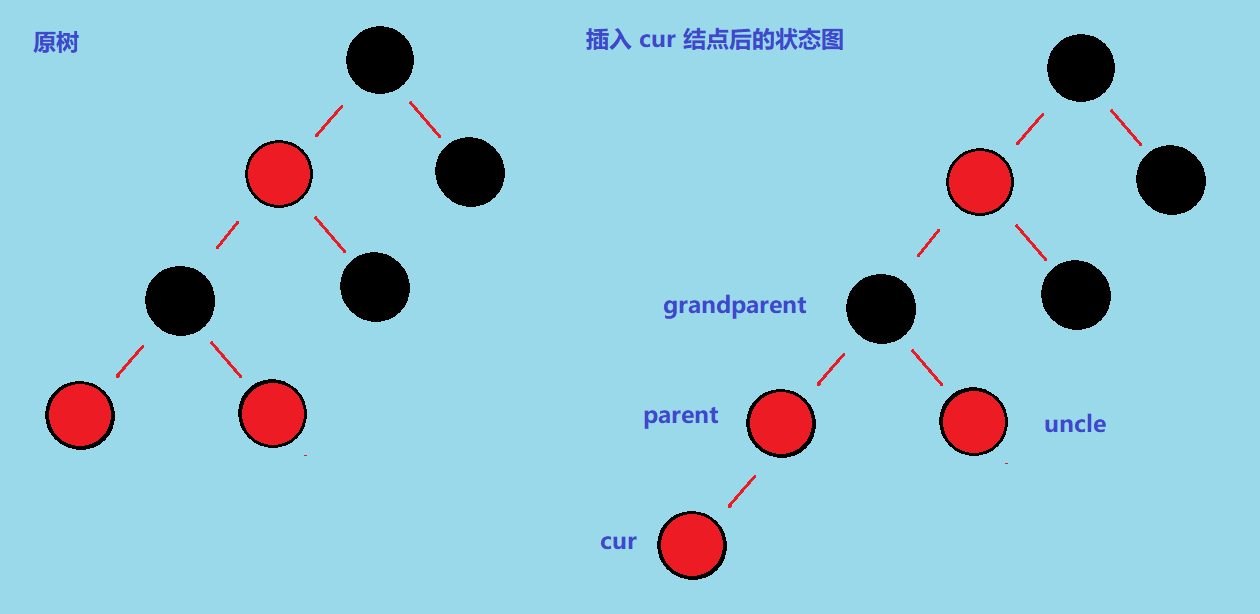很明显这触发了状态 1.1，我们需要调整 parent.color = BLACK; uncle.color = BLACK; grandparent.color = RED;然后再调整 cur 和 parent 的引用位置，方便继续向上调整： cur = grandparent; parent = cur.parent ，就是下面这种情况
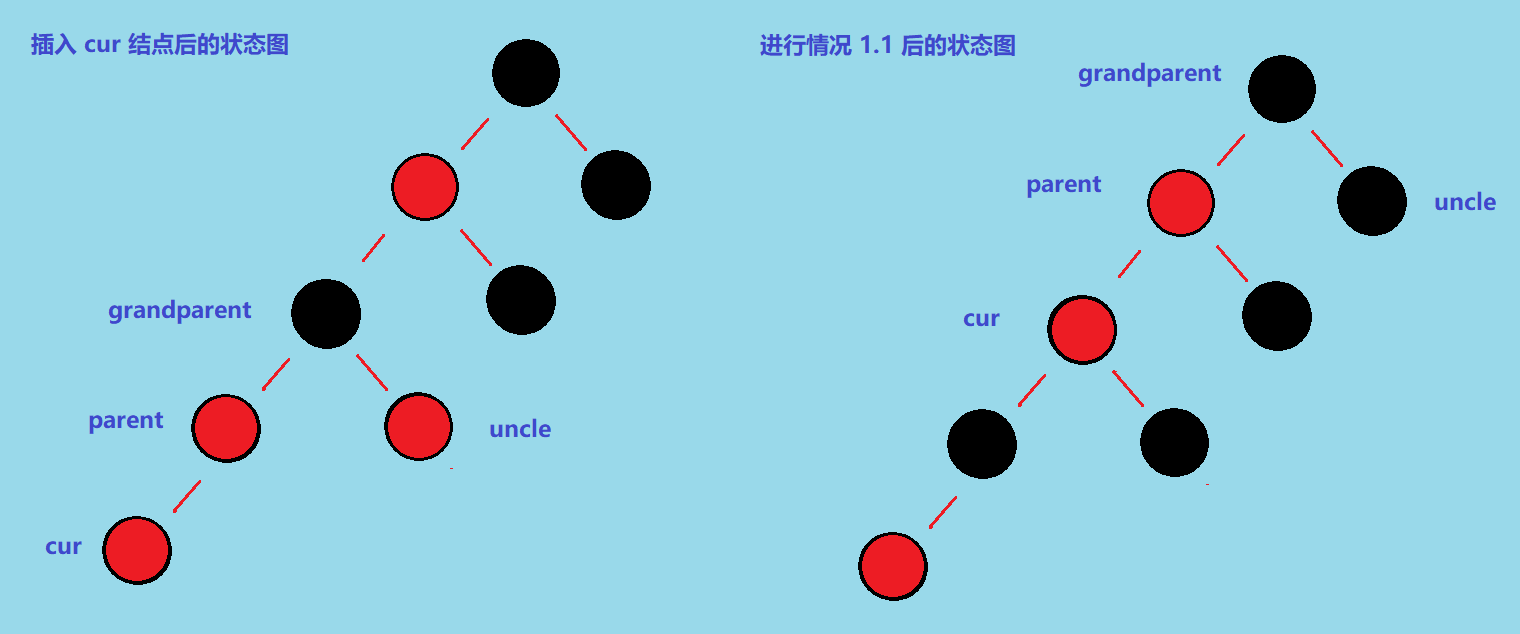
这就是「调整红黑树过程中出现的情况 1.2」
情况 1.2: uncle == null || uncle.color == BLACK, 并且 cur == parent.left
（这里需要用到右旋，不了解右旋的建议先学一下 AVL 树，可以参考我上一篇博客AVL的旋转）
这种情况下我们就要对 grandparent 进行右旋，然后将 grandparent 变为红色，parent 变为黑色，如下
情况 1.3
这种情况也是建立在上一情况的 else 语句中的 —— uncle == null || uncle.color = BLACK，这也是出现在调整过程中的
但是情况 1.3 中， cur 是 parent 的右孩子，这种情况可以通过左旋转换成情况 1.2，我们来具体看看
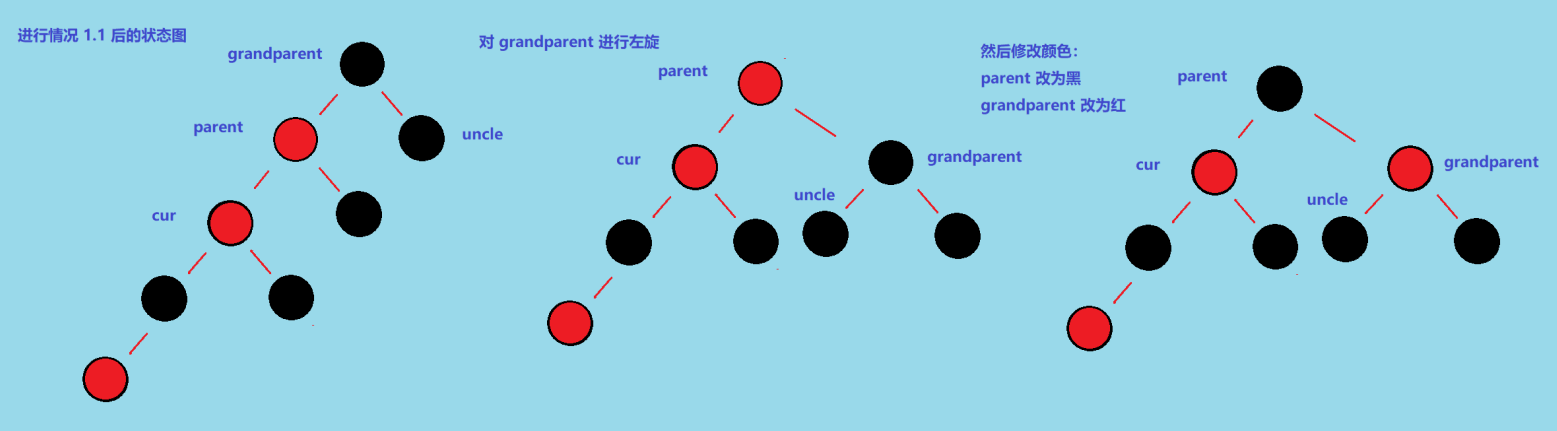
例如下图是情况 1.3
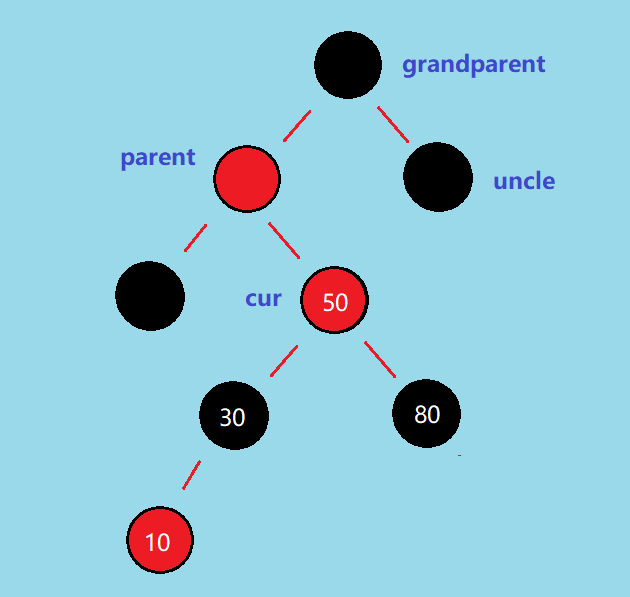
首先需要对 parent 进行左旋 👇：
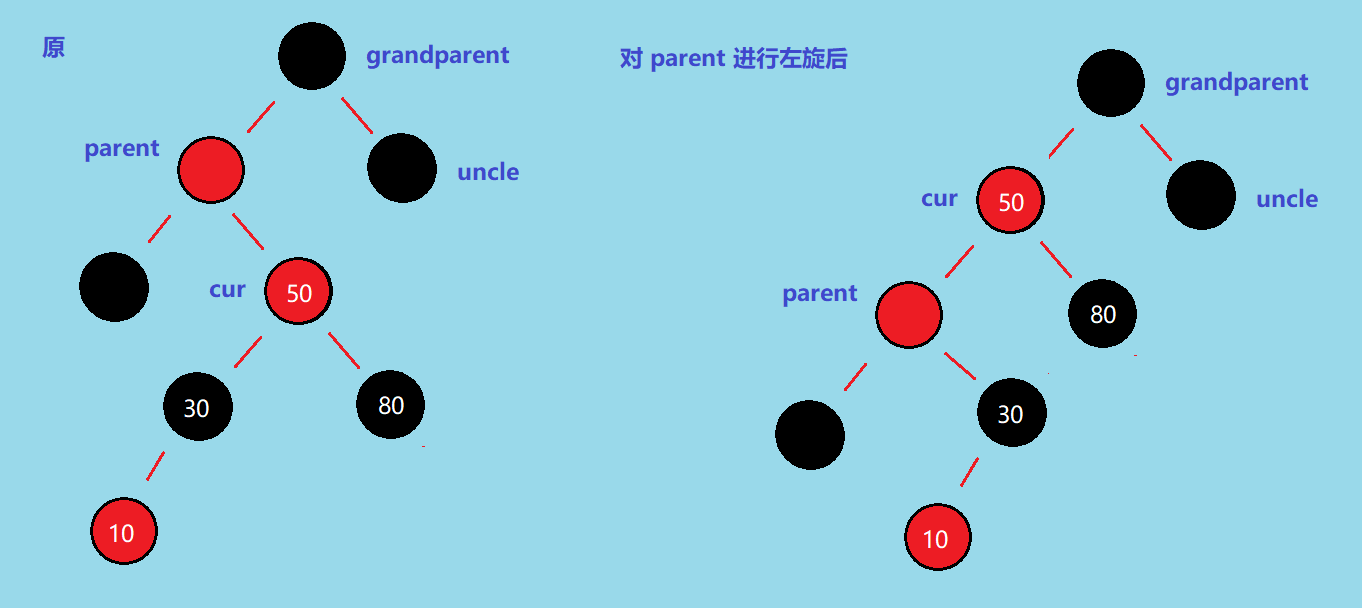好，现在我们将这个左旋后的图和情况 1.2 的图对比一下 👇，除了最下方的孩子结点位置不太一样之外，还有 cur 和 parent 的引用反了，所以这里我们将左图中的 parent 和 cur 交换一下引用就可以变成需要进行情况 1.2 操作的状态
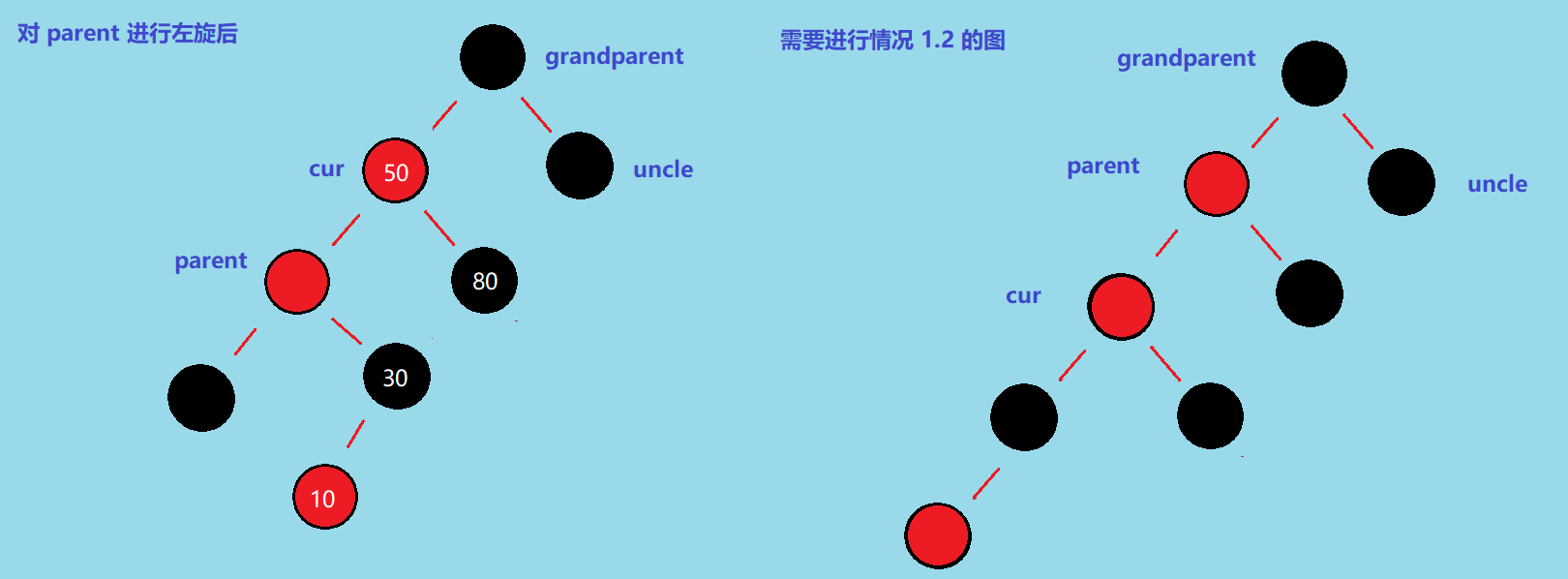
所以对于情况 1.3 我们只需要进行左旋 + 交换 cur 和 parent 引用就可以变成情况 1.2 了 ！，于是再交给 情况 1.2 处理即可
至此就是情况 1 的全部情况了, 以下是情况 1 的代码
// 插入一个新节点
public boolean insert(int val) {
RBTreeNode newNode = new RBTreeNode(val);
if (root == null) {
root = newNode;
root.color = BLACK; // 根节点颜色为 黑
return true;
}
// 寻找插入位置
RBTreeNode parent = null;
RBTreeNode cur = root;
while (cur != null) {
if (cur.val < val) {
parent = cur;
cur = cur.right;
} else if (cur.val > val) {
parent = cur;
cur = cur.left;
} else {
return true; // 重复节点
}
}
// 至此 cur 为空，parent 为 cur 的父节点
// 完成节点的插入
if (parent.val > val) {
parent.left = newNode;
} else {
parent.right = newNode;
}
newNode.parent = parent; // 双向连接
// parent = cur.parent;
cur = newNode;
// 至此开始「向上调整颜色」
// 新插入的结点是红色的, 如果父亲结点还是红色的, 就需要调整颜色
while (parent != null && parent.color == RED) {
// 定义祖父结点
RBTreeNode grandparent = parent.parent; // 因为根节点必须是黑色, 所以祖父结点不可能为空
// 第一种情况, parent 是 grandparent 的 左孩子
if (parent == grandparent.left) {
RBTreeNode uncle = grandparent.right;
// 情况 1.1: parent 红色, uncle 不为空, 并且红色
if (uncle != null && uncle.color == RED) {
parent.color = BLACK;
uncle.color = BLACK;
grandparent.color = RED; // 修改颜色
cur = grandparent;
parent = cur.parent;
} else {
// 这里有还有两种情况
// 情况 1.3: cur 是 parent 的右孩子, 并且 uncle 为空, 或者 uncle 为黑色
// 左旋后交换引用就可以变成情况 1.2
if (cur == parent.right) {
// 这时候需要先左旋
rotateLeft(parent);
RBTreeNode temp = parent;
parent = cur;
cur = temp;
}
// 情况 1.2: cur 是 parent 的左孩子, 并且 uncle 为空, 或者 uncle 为黑色
// 需要 向右旋转
rotateRight(grandparent);
// 再修改颜色
grandparent.color = RED;
parent.color = BLACK;
}
} else {
// 情况 2
}
}
root.color = BLACK;// 插入操作结束前再将 root 改为黑色
}
情况 2.0
情况 2.0 和 情况 1.0 是很像的, 基本上改个方向就对了, 我们再简单过一次
既然进入了 2.0 情况, 那么就是进入了 else 语句了，也就是这种情况
parent == grandparent.right
情况 2.1
和 1.1 一样， 也就是当：
if (uncle != null && uncle.color == RED)
对应着这种情况
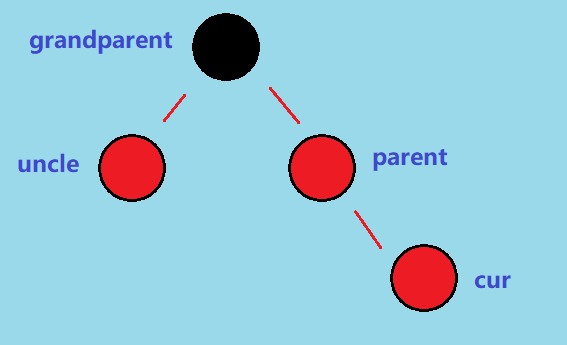
此时我们需要将 uncle 和 parent 都改成黑色，并且由于 grandparent 可能是有父亲的，而且不知道是黑色还是红色，如果父亲结点是 黑色，那么我们再将 grandparent 改成红色就可以了。但是如果是红色，将 grandparent 改成红色虽然可能没法直接符合黑红树的性质，但是这样能够通过触发其他情况来解决。
所以做法是：将 parent 和 uncle 改成黑色，将 grandparent 改成红色，等到插入即将结束的时候，再将 grandparent 改成黑色（防止根节点是红色）
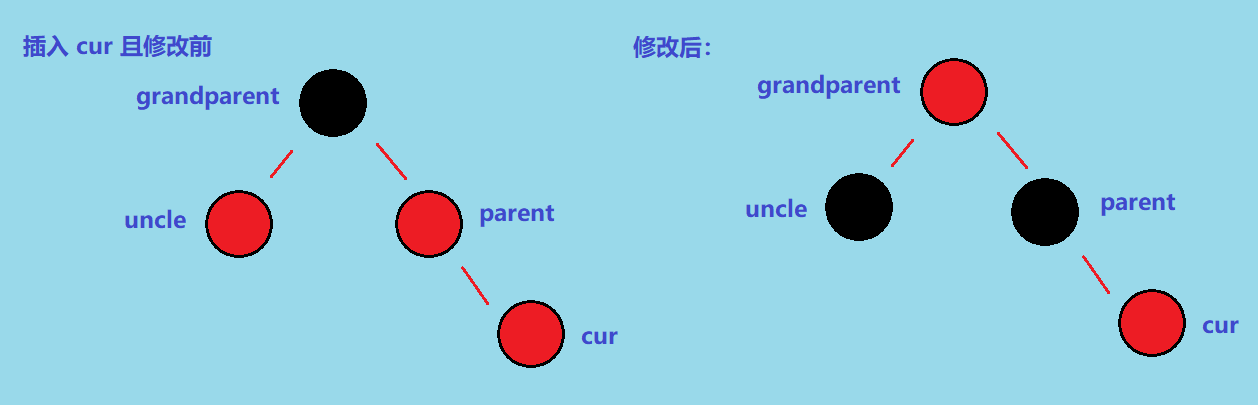
情况 2.2
if (uncle == null || uncle.color == BLACK)
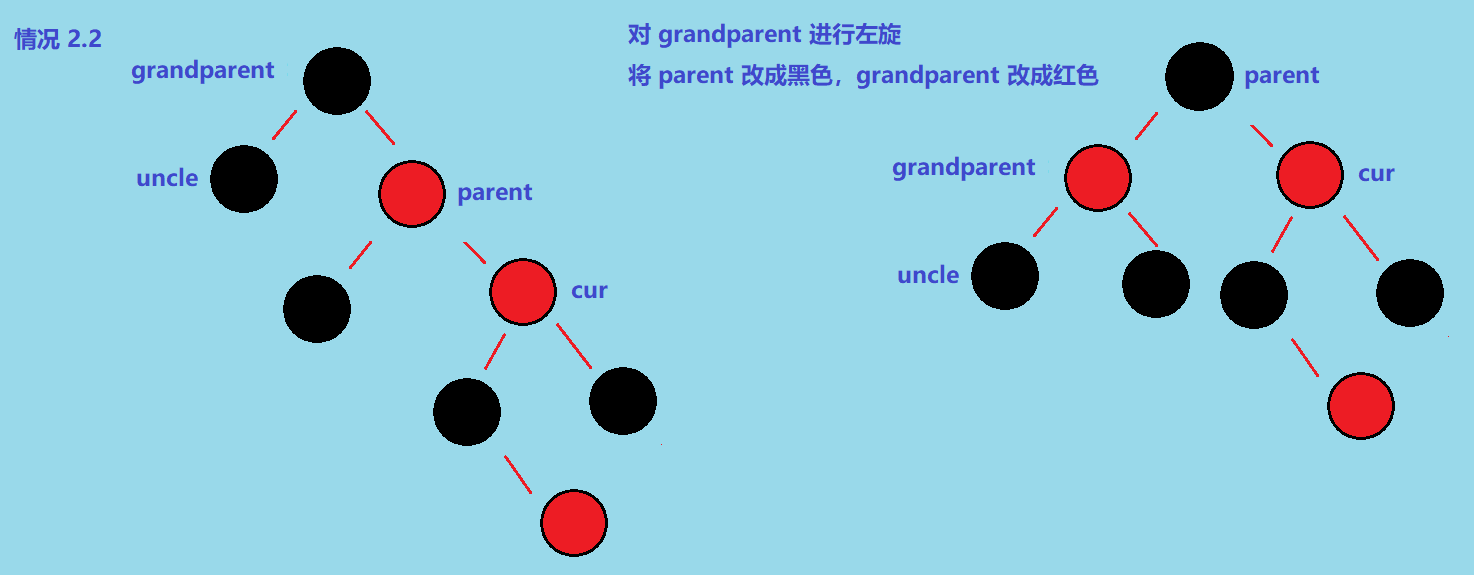
该情况状态图和 2.2 也很像，直接给出需要进行情况 2.2 的图 👇
操作步骤是：左旋后修改 grandparent 和 parent 的颜色
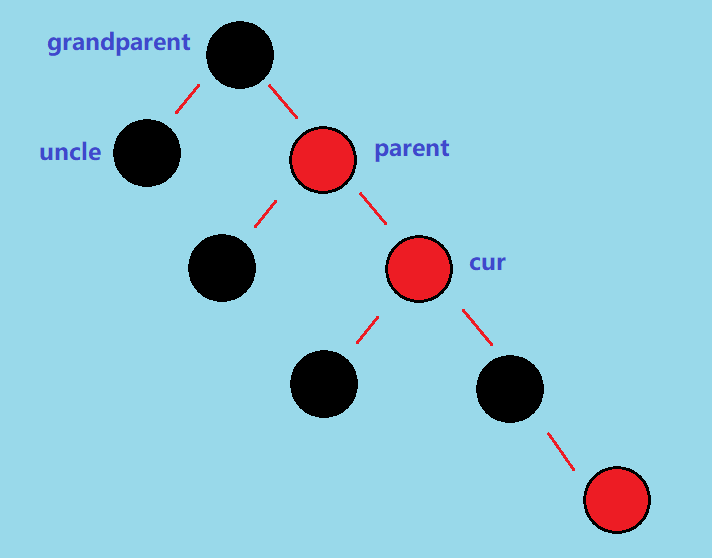
具体操作如下：
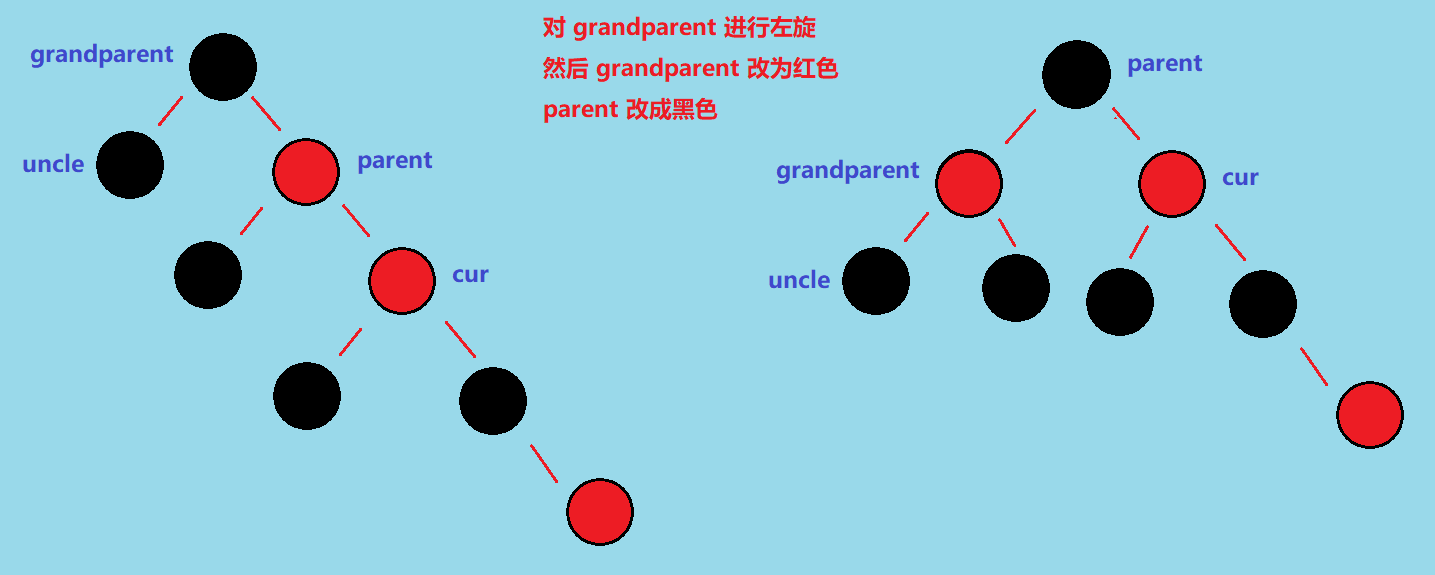
情况 2.3
这个情况的触发条件和 2.2 很像，但是 cur 还需要是 parent 的左孩子，这样的话可以通过其他操作再触发 2.2 的状态
if (cur == parent.left)
if (uncle == null || uncle.color == BLACK)
状态图如下：
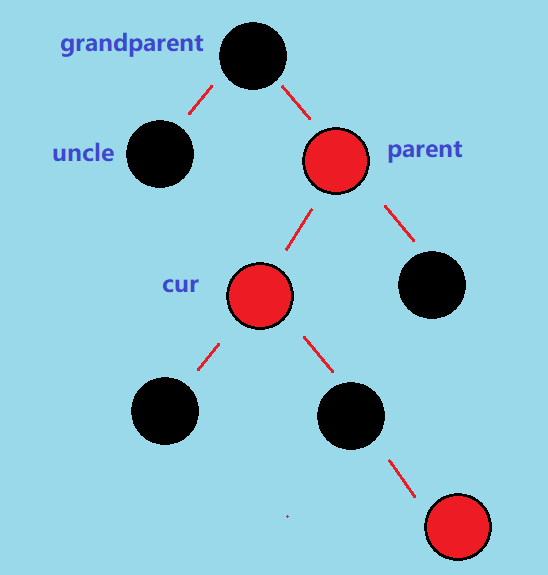
操作步骤：先对 parent 进行右旋，然后交换 parent 和 cur 引用，就可以变成情况 2.2 了
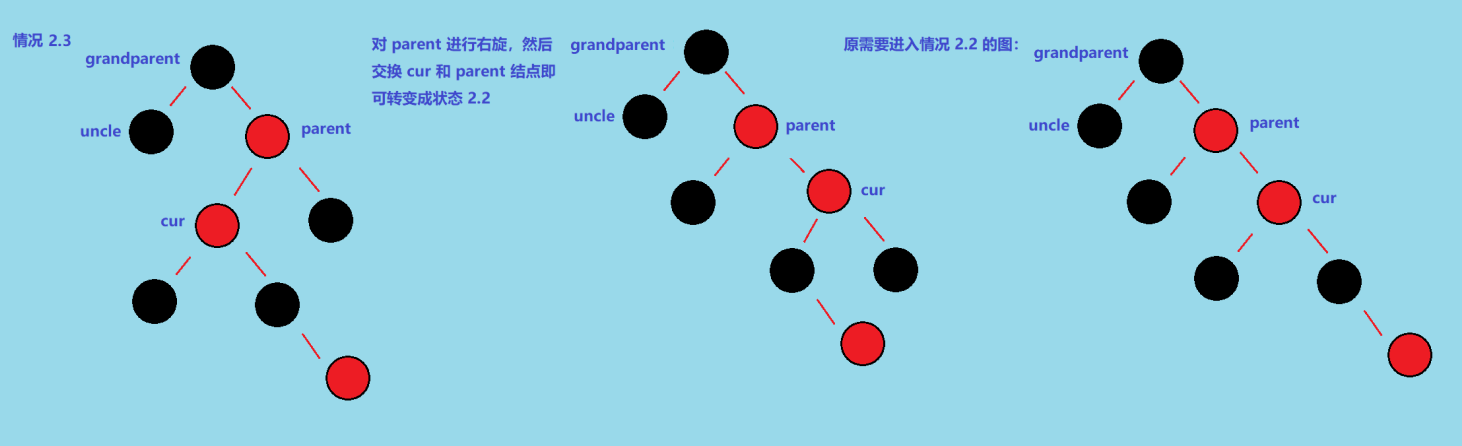
再进行 情况 2.2 要进行的操作即可
至此情况 2.0 也结束了
情况 2.0 的代码：
else {
// parent = grandparent.right;
RBTreeNode uncle = grandparent.left;
if (uncle != null && uncle.color == RED) {
parent.color = BLACK;
uncle.color = BLACK;
grandparent.color = RED; // 先变为 红色, 方便后续操作, 最后再统一变成 黑色
} else {
if (cur == parent.left) {
rotateRight(parent);
RBTreeNode temp = parent;
parent = cur;
cur = temp;
}
rotateLeft(grandparent);
grandparent.color = RED;
parent.color = BLACK;
}
}
插入过程完整代码如下：
完整代码
public class RBTree {
private static class RBTreeNode {
private RBTreeNode parent;
private RBTreeNode left;
private RBTreeNode right;
private COLOR color;
int val ;
public RBTreeNode(int val) {
this.val = val;
// 新节点默认都为 红色
this.color = RED;
}
}
public RBTreeNode root ;
// 插入一个新节点
public boolean insert(int val) {
RBTreeNode newNode = new RBTreeNode(val);
if (root == null) {
root = newNode;
root.color = BLACK; // 根节点颜色为 黑
return true;
}
// 寻找插入位置
RBTreeNode parent = null;
RBTreeNode cur = root;
while (cur != null) {
if (cur.val < val) {
parent = cur;
cur = cur.right;
} else if (cur.val > val) {
parent = cur;
cur = cur.left;
} else {
return true; // 重复节点
}
}
// 至此 cur 为空，parent 为 cur 的父节点
// 完成节点的插入
if (parent.val > val) {
parent.left = newNode;
} else {
parent.right = newNode;
}
newNode.parent = parent; // 双向连接
// parent = cur.parent;
cur = newNode;
// 至此开始「向上调整颜色」
// 新插入的结点是红色的, 如果父亲结点还是红色的, 就需要调整颜色
while (parent != null && parent.color == RED) {
// 定义祖父结点
RBTreeNode grandparent = parent.parent; // 因为根节点必须是黑色, 所以祖父结点不可能为空
// 第一种情况, parent 是 grandparent 的 左孩子
if (parent == grandparent.left) {
RBTreeNode uncle = grandparent.right;
// 情况 1.1: parent 红色, uncle 不为空, 并且红色
if (uncle != null && uncle.color == RED) {
parent.color = BLACK;
uncle.color = BLACK;
grandparent.color = RED; // 修改颜色
cur = grandparent;
parent = cur.parent;
} else {
// 这里有还有两种情况
// 情况 1.3: cur 是 parent 的右孩子, 并且 uncle 为空, 或者 uncle 为黑色
if (cur == parent.right) {
// 这时候需要先左旋
rotateLeft(parent);
RBTreeNode temp = parent;
parent = cur;
cur = temp;
}
// 情况 1.2: cur 是 parent 的左孩子, 并且 uncle 为空, 或者 uncle 为黑色
// 需要 向右旋转
rotateRight(grandparent);
// 再修改颜色
grandparent.color = RED;
parent.color = BLACK;
}
} else {
// parent = grandparent.right;
RBTreeNode uncle = grandparent.left;
if (uncle != null && uncle.color == RED) {
parent.color = BLACK;
uncle.color = BLACK;
grandparent.color = RED; // 先变为 红色, 方便后续操作, 最后再统一变成 黑色
} else {
if (cur == parent.left) {
rotateRight(parent);
RBTreeNode temp = parent;
parent = cur;
cur = temp;
}
rotateLeft(grandparent);
grandparent.color = RED;
parent.color = BLACK;
}
}
}
// 最后再将根节点统一修改为 黑色
root.color = BLACK;
return true;
}
// 左旋
private void rotateLeft(RBTreeNode parent) {
RBTreeNode rson = parent.right;
RBTreeNode rsonLeft = rson.left;
RBTreeNode grandparent = parent.parent;
parent.right = rsonLeft;
if (rsonLeft != null) {
rsonLeft.parent = parent;
}
parent.parent = rson;
rson.left = parent;
if (root == parent) {
root = rson;
rson.parent = null;
} else {
if (grandparent.right == parent) {
grandparent.right = rson;
} else {
grandparent.left = rson;
}
rson.parent = grandparent;
}
}
// 右旋
private void rotateRight(RBTreeNode parent) {
RBTreeNode lson = parent.left;
RBTreeNode lsonRight = lson.right;
RBTreeNode grandparent = parent.parent;
parent.left = lsonRight;
if (lsonRight != null) {
lsonRight.parent = parent;
}
lson.right = parent;
parent.parent = lson;
if (root == parent) {
root = lson;
lson.parent = null;
} else {
if (grandparent.left == parent) {
grandparent.left = lson;
} else {
grandparent.right = lson;
}
lson.parent = grandparent;
}
}
}
红黑树的检验
要检验一棵树是不是红黑树，我们就判断这棵树是不是符合红黑树的所有性质就好了
- 结点只有红，黑两种属性（显而易见对吧，红黑树嘛）
- 根节点为黑色
- 叶子结点视为黑色，这里的叶子结点指的是最底层的空节点
- 不能存在两个连续的红色节点
- 从「任意节点开始到其后代叶子节点」简单的路径上，有「相同数量的黑色节点」
根节点为黑色
只需要在函数开头特殊判断一下即可
不能存在两个连续的结点
通过递归实现即可，如果当前结点为红色，那就判断一下父亲结点是不是红色，如果是，那就返回 false
// 判断有没有 两个连续 的红色节点
public boolean checkRedNode(RBTreeNode root) {
if (root == null) return true;
if (root.color == RED) {
if (root.parent != null && root.parent.color == RED) {
return false;
}
}
return checkRedNode(root.left) && checkRedNode(root.right);
}
从「任意节点开始到其后代叶子节点」简单的路径上，有「相同数量的黑色节点」
我们依旧可以递归实现这个验证，这个递归的方法体为：
public boolean checkBlackNode(RBTreeNode root, int pathBlackNum, int neededBlackNum)
pathBlackNum 是当前路径上黑色结点个数，neededBlackNum 是以某一条路径为准的黑色结点个数，如果某条路径上的 pathBlackNum != neededBlackNum ，那就不是红黑树。
如何计算 neededBlackNum ? 我们可以以这棵红黑树最左边的那条路径为准，这样的话就有多种计算方法
- 我们可以在进入这个函数之前，再把最左边的那条路径上的黑色结点算出来，然后把这个值传参传给 neededBlackNum
- 也可以直接将 -1 传给 neededBlackNum，如果某条路径走完了，neededBlackNum 还是 -1，那就说明这个路径是第一次达到的，就将
neededBlackNum = pathBlackNum，而 needBlackNum 不为 -1了，说明已经有一条路径上的黑色结点数被算出来了，以这个值为基准进行比较即可
/**
* 检查黑色的结点符不符合要求
* @param pathBlackNum 当前路径的 黑色结点数, 刚开始默认是 -1, 第一次到达更结点的时候更新 neededBlackNum
* @param neededBlackNum 总共需要的黑色结点数量
*/
public boolean checkBlackNode(RBTreeNode root, int pathBlackNum, int neededBlackNum) {
if (root == null) return true;
if (root.color == BLACK) {
pathBlackNum ++;
}
// 到达根节点的时候检查一下
if (root.left == null && root.right == null) {
if (neededBlackNum == -1) { // 第一次走完一条完整路径的时候, 更新一下 neededBlackNum
neededBlackNum = pathBlackNum;
} else { // pathBlackNum 更新完了
if (neededBlackNum != pathBlackNum) { // 不相等就不是了
return false;
}
}
}
// 左子树和右子树都要满足题意
return checkBlackNode(root.left, pathBlackNum, neededBlackNum) && checkBlackNode(root.right, pathBlackNum, neededBlackNum);
}
验证代码和用例
这里先提供一个用例
int[] array = {4, 2, 6, 1, 3, 5, 15, 7, 16,14};
RBTree rbTree = new RBTree();
for (int i = 0; i < array.length; i++) {
rbTree.insert(array[i]);
}
除此之外，我们也可以中序遍历一下，看一下是不是有序的。上总代码：
// 判断一棵树 是不是 红黑树
public boolean isRBTree() {
if (root == null) return true;
if (root.color != BLACK) { // 根节点必须为 黑色
return false;
}
// 分别检查红色 和 黑色结点合不合格
return checkRedNode(root) && checkBlackNode(root, 0, -1);
}
// 判断有没有 两个连续 的红色节点
public boolean checkRedNode(RBTreeNode root) {
if (root == null) return true;
if (root.color == RED) {
if (root.parent != null && root.parent.color == RED) {
return false;
}
}
return checkRedNode(root.left) && checkRedNode(root.right);
}
/**
* 检查黑色的结点符不符合要求
* @param pathBlackNum 当前路径的 黑色结点数, 刚开始默认是 -1, 第一次到达更结点的时候更新 neededBlackNum
* @param neededBlackNum 总共需要的黑色结点数量
*/
public boolean checkBlackNode(RBTreeNode root, int pathBlackNum, int neededBlackNum) {
if (root == null) return true;
if (root.color == BLACK) {
pathBlackNum ++;
}
// 到达叶子节点的时候检查一下
if (root.left == null && root.right == null) {
if (neededBlackNum == -1) { // 第一次走完一条完整路径的时候, 更新一下 neededBlackNum
neededBlackNum = pathBlackNum;
} else { // 否则已经有某一条路径走完了
if (neededBlackNum != pathBlackNum) {
return false;
}
}
}
return checkBlackNode(root.left, pathBlackNum, neededBlackNum) && checkBlackNode(root.right, pathBlackNum, neededBlackNum);
}
// 中序遍历观察是否是有序的
public void inorder(RBTreeNode root) {
if(root == null) {
return;
}
inorder(root.left);
System.out.print(root.val + " ");
inorder(root.right);
}
完
