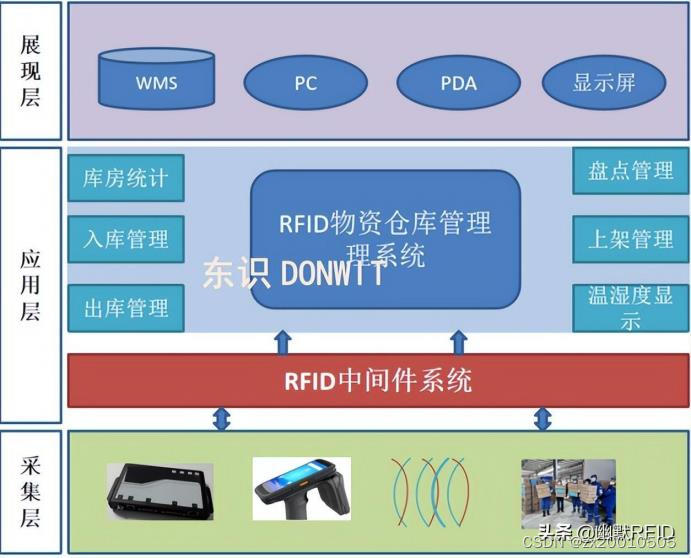
前向传播Forward propagation

前向传播算法就是： 将上一层的输出作为下一层的输入，并计算下一层的输出，一直到运算到输出层为止

在正式介绍前向传播前，先简单介绍计算图（Computational Graph）的概念。

$$\mathrm{y}=\mathrm{w}\ast \mathrm{x}+\mathrm{b}$$

可以用下面的有向无环图表示。

假设一个三层的神经网络，有两个输入和一个输出，每一个层都是全连接层和激活函数层

第一层输入为

$$Y^{(1)}=X^{(1)}{W}^{(1)}+b^{(1)}$$

$$\left[\begin{array}{llll}{y}_{1,1}^{(1)}& y_{1,2}^{(1)}& y_{1,3}^{(1)}& y_{1,4}^{(1)}\end{array}\right]=\left[\begin{array}{ll}{x}_{1,1}^{(1)}& x_{1,2}^{(1)}\end{array}\right]\left[\begin{array}{llll}{w}_{1,1}^{(1)}& w_{1,2}^{(1)}& w_{1,3}^{(1)}& w_{1,4}^{(1)}\\ w_{2,1}^{(1)}& w_{2,2}^{(1)}& w_{2,3}^{(1)}& w_{2,4}^{(1)}\end{array}\right]+\left[\begin{array}{llll}{b}_{1,1}^{(1)}& b_{1,2}^{(1)}& b_{1,3}^{(1)}& b_{1,4}^{(1)}\end{array}\right]$$

其中w和b的数值是神经网络通过学习得到的

之后我们可以得到第一层的输出，第一全连接层的运算过程

$$\left[\begin{array}{llll}1.12& 1.28& 0.32& -0.36\end{array}\right]=\left[\begin{array}{ll}0.4& 0.6\end{array}\right]\left[\begin{array}{cccc}1.1& -0.3& -0.1& -0.6\\ -0.2& 0.5& 1.1& -0.2\end{array}\right]+\left[\begin{array}{llll}0.8& 1.1& -0.3& 0.0\end{array}\right]$$

接着是激活函数层，激活函数用于提供非线性性，我们以ReLU函数为例

https://baike.baidu.com/item/ReLU 函数/22689567

$$y=\mathrm{ReLU}(x)=\{\begin{array}{ll}0,& x<0\\ x,& x⩾0\end{array}$$

ReLU函数相当于保留正值,将负值强制置0

第二层输出为

$$Y^{(2)}=X^{(2)}{W}^{(2)}+b^{(2)}$$

$$\left[\begin{array}{llll}{y}_{1,1}^{(2)}& y_{1,2}^{(2)}& y_{1,3}^{(2)}& y_{1,4}^{(2)}\end{array}\right]=\left[\begin{array}{llll}{x}_{1,1}^{(2)}& x_{1,2}^{(2)}& x_{1,3}^{(2)}& x_{1,4}^{(2)}\end{array}\right]\left[\begin{array}{cccc}{w}_{1,1}^{(2)}& w_{1,2}^{(2)}& w_{1,3}^{(2)}& w_{1,4}^{(2)}\\ w_{2,1}^{(2)}& w_{2,2}^{(2)}& w_{2,3}^{(2)}& w_{2,4}^{(2)}\\ w_{3,1}^{(2)}& w_{3,2}^{(2)}& w_{3,3}^{(2)}& w_{3,4}^{(2)}\\ w_{4,1}^{(2)}& w_{4,2}^{(2)}& w_{4,3}^{(2)}& w_{4,4}^{(2)}\end{array}\right]+\left[\begin{array}{llll}{b}_{1,1}^{(2)}& b_{1,2}^{(2)}& b_{1,3}^{(2)}& b_{1,4}^{(2)}\end{array}\right]$$

x2的值由上一层的输出得到，最后得到第二全连接层的输出

在经过激活函数层

最后一层为输出层

$$\left[\begin{array}{l}{y}_{1,1}^{(3)}\end{array}\right]=\left[\begin{array}{llll}{x}_{1,1}^{(3)}& x_{1,2}^{(3)}& x_{1,3}^{(3)}& x_{1,4}^{(3)}\end{array}\right]\left[\begin{array}{l}{w}_{1,1}^{(3)}\\ w_{2,1}^{(3)}\\ w_{3,1}^{(3)}\\ w_{4,1}^{(3)}\end{array}\right]+\left[b_{1,1}^{(3)}\right]$$

最终输出为

这就是整个网络的前向传播过程