通过公钥加密系统,可以对传输于两个通信单位之间的消息进行加密,即使窃听者窃听到加密之后的消息,也不能对其破译。
1、RSA公钥加密原理
1.1 几个核心概念
- 公钥P与公钥函数P()
- 密钥S与密钥函数S()
可以简单理解,一个公钥对应一个公钥函数,知道了公钥也就知道了公钥函数。一个密钥也是对应一个密钥函数。我们要传输的信息M,经过公钥函数P()之后,就成了密文C,然后密文C经过密钥函数S()解密之后,就可以还原成密文M。
由于公钥、公钥函数以及密钥、密钥函数是一一对应的,后续叙述中不再区分,即默认知道公钥,也就知道了公钥函数。
加密系统中,每个参与者,都有自己的公钥和密钥,公钥(公钥函数)是对外公开的,密钥是不对外公开的(这是加密的前提)。
公钥函数和密钥函数互为反函数,即对于任意一条消息M,有:
M = S(P(M))
M = P(S(M))
也就是说,无论哪种顺序,运用两把钥匙P和S对消息M进行变换之后,可以还原消息M。这是加密的基本原理。
1.2 RSA公钥加密系统中遵守的原则和假设
- 系统每个参与者都有自己的公钥和密钥
- 公钥对外公开,密钥只有自己知道
- 其他人不能根据公钥P推断除密钥S
1.3 公钥加密信息传输过程
在公钥加密系统中,信息的接受方(假设为Alice),需要给信息的发送方(假设为Bob)提供公钥。右一般来说,在一个公钥加密系统中,每个参与者的公钥都是公开的(放在一个公开的目录)。记住一个关键点:
公钥加密消息传递中,接受方提供公钥,发送方使用接受方提供的公钥进行加密,然后发送。
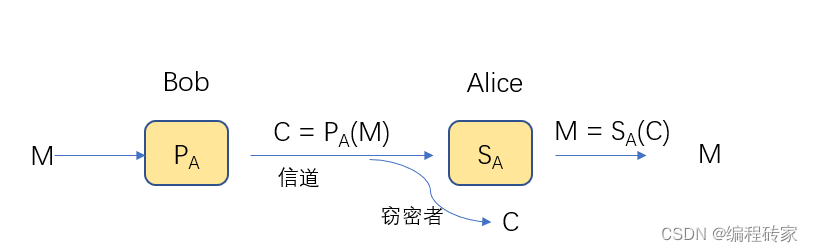
假如Bob需要给Alice发送加密消息,那么Bob需要先获取Alice的公钥PA。然后使用公约PA对消息M进行加密,然后将加密的消息发送给Alice,然后Alice使用自己的密钥SA进行解密,然后就可以获得消息M了。由于密钥SA只有Alice自己知道,因此即使窃密者获取了密文C,由于不知道密钥SA,也无法对获取的密文C解密。
1.4 数字签名实现的原理与过程
在公钥系统的设想中,很容易实现数字签名。假如现在Alice希望把一个数字签署的答复M’发送给Bob。
- Alice运用自己的密钥对签名进行加密
- Alice将加密后的信息,即数字签名以及消息M‘一同发送给Bob
- Bob收到数字签名之后,运用Alice的公钥进行解密,判断得到的消息是否来自Alice(假如消息M‘包含Alice的名字,那么Bob就知道该使用谁的公钥)
- 如果等式成立,那么Bob就知道M’确实是来自Alice,否则就认为是伪造的签名。
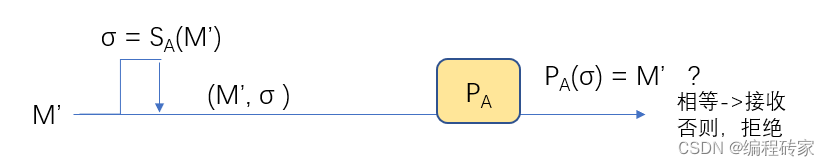
这里判断的一个基本逻辑就是,只有数字签名是通过Alice的密钥加密得到的,那么对数字签名运用Alice的公钥PA解密之后,才能得到消息M’。
那么想象一下,有没有可能一个伪造的签名,运用Alice的公钥解密之后也能得到消息M‘呢?
– – 这是不可能的,因为能够通过一种方法F伪造一个数字签名Q,并且签名Q经过Alice的公钥运算之后还能得到M’,那么有如下关系:

说明F就是PA的反函数,那么PA的反函数为SA,说明F就是SA,根据1.3中假设,是不能通过公钥P得到密钥S的,因此这就保证了不能产生伪造的签名。
1.5 数字签名和公钥加密的异同
同:
- 使用同一套加密系统,都是信息发送者对信息进行加密,然后接受者对信息进行解密。
异:
从目的上来讲,公钥加密是为了保证发送信息的私密性,即信息只有接受者可以获取正确信息,其他人不能获取。而数字签名,主要目的是别人验证这个信息来源是否正确,签名的内容可以是公开的(没有私密性), 也可不公开。
从加密过程来讲,公钥加密使用的接受方的公钥和密钥,而数字签名使用的发送方的公钥和密钥。
公钥加密是发送者运用信息接收方的公钥进行加密,然后接受者用自己的密钥解密。数字签名,是发送者用自己的密钥加密,接收者(需要验证信息的人)运用发送方的公钥进行加密。
1.6 公钥加密与数字签名结合使用
1.4中签属的信息是公开的、没有加密受到保护的。如果把公钥加密与数字签名结合起来使用,就可以创造出同时被签属和加密的信息:
- 只有接收者才能接受到消息签署的消息
- 接收者可以验证签属的信息来源是否正确
具体做法如下:
- 签属者(发送方)运用自己的密钥(发送方密钥)对消息M’进行运算得到签名Q,
- 发送方将消息M‘以及得到的签名Q一起作为整体消息M,使用接受方的公钥进行加密,得到密文C
- 发送方将密文C发送给接受方
- 接受方队密文C,运用自己的密钥(接收方密钥)进行解密,得到消息M(包含M’以及Q)
- 接受方对解密后的消息Q使用发送方公钥进行运算,判断结果是否等于M’, 若等于则接受,否则拒绝
2 RSA加密系统的具体实现
通过上面的内容可以发现,要实现一个RSA加密系统,其实就是需要给参与者创建一对公钥和密钥。
由于RAS加密系统在创建公钥和密钥的过程中,涉及到很多一些数论概念,推导过程也需要用到一些数论中的结论,有些麻烦和晦涩。这里仅给出创建过程和结论:
- 公钥P = (e, n), 对外公开,作为参与者的RSA公钥
- 密钥S = (d, n), 保密,作为参与者的RSA密钥
一对公钥密钥涉及到三个参数e、d、n。
其中获得过程如下:
1、选取两个很大素数p和q, pq很多可能上千位
2、计算 n = pq
3、选取一个与k = (p-1)(q-1) 互质的小jing奇数e
4、对模k,计算e的乘法逆元d的值
知道公钥和密钥之后,对应的公钥方法和密钥方法也就确定了:

解密的原理(证明过程省略。。。):

上面的式子说明,无论说明顺序,一条消息经过公钥和密钥变换之后,可以将加密后的消息还原(解密)。