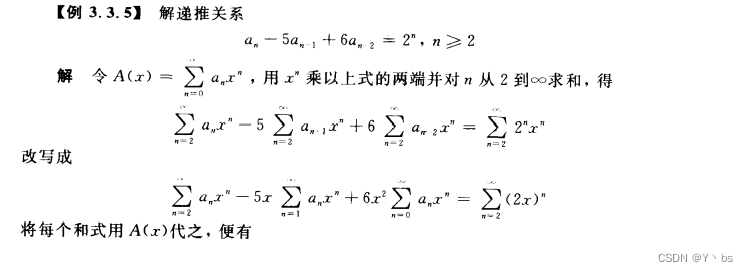文章目录
- 三、递推关系
- 3.1 常系数线性递推关系
- 特征根法
- 1.齐次递推关系
- 2.非齐次方程
- 母函数方法
三、递推关系
3.1 常系数线性递推关系
k 阶 齐 次 递 推 关 系 : a n + c 1 a n − 1 + c 2 a n − 2 + . . . + c k a n − k = 0 , c k ≠ 0 ( 3.1.1 ) k 阶 非 齐 次 递 推 关 系 : a n + c 1 a n − 1 + c 2 a n − 2 + . . . + c k a n − k = f ( n ) , c k ≠ 0 ( 3.1.2 ) k阶齐次递推关系: \quad a_n+c_1a_{n-1}+c_2a_{n-2}+...+c_ka_{n-k}=0,c_k≠0 \quad \quad(3.1.1)\\ \\ k阶非齐次递推关系: a_n+c_1a_{n-1}+c_2a_{n-2}+...+c_ka_{n-k}=f(n),c_k≠0 \quad \quad (3.1.2)\\ k阶齐次递推关系:an+c1an−1+c2an−2+...+ckan−k=0,ck=0(3.1.1)k阶非齐次递推关系:an+c1an−1+c2an−2+...+ckan−k=f(n),ck=0(3.1.2)
特征根法
1.齐次递推关系
1.1. 特征根为单根
设q1,q2,…,qn是式(3.1.1)的互不相同的特征根,则式(3.1.1)的通解为
a
n
=
A
1
q
1
n
+
A
2
q
2
n
+
.
.
.
+
A
k
q
k
n
a_n=A_1q_1^n+A_2q_2^n+...+A_kq_k^n \quad\quad
an=A1q1n+A2q2n+...+Akqkn
例题

1.2. 重根情况
一般情况下,设q是式(3.2.1)的k重解,则,式(3.1.1)的通解为
a
n
=
(
A
1
+
A
2
n
+
.
.
.
+
A
k
n
k
−
1
)
q
n
a_n=(A_1+A_2n+...+A_kn^{k-1})q^n
an=(A1+A2n+...+Aknk−1)qn
1.3. 复根情况
一般情况,设q是m重复根,自然q’也是m重复根,则通解为
ρ
n
[
(
A
1
+
A
2
n
+
.
.
.
+
A
m
n
m
−
1
)
c
o
s
(
n
θ
)
+
(
B
1
+
B
2
n
+
.
.
.
+
B
m
n
m
−
1
)
s
i
n
(
n
θ
)
]
ρ^n[(A_1+A_2n+...+A_mn^{m-1})cos(nθ)+(B_1+B_2n+...+B_mn^{m-1})sin(nθ)]
ρn[(A1+A2n+...+Amnm−1)cos(nθ)+(B1+B2n+...+Bmnm−1)sin(nθ)]
例题

2.非齐次方程
设a*是式(3.1.2)的一个特解,a’n是式(3.1.1)的通解,则式(3.1.2)的通解为
a
n
=
a
n
∗
+
a
^
n
a_n=a_n^*+\hat{a}_n
an=an∗+a^n
2.1. f(n) = b (b为常数)
a
n
∗
=
A
n
m
a_n^*=An^m
an∗=Anm
其中,m表示1是式(3.1.1)的m重特征根(0≤m≤k),若1不是特征根(即m=0)
a
n
∗
=
A
a_n^*=A
an∗=A
例题

2.2. f(n) = b^n (b为常数)
a
n
∗
=
A
n
m
n
n
a_n^*=An^mn^n
an∗=Anmnn
其中m表示b是式(3.1.1)的m重特征根(0≤m≤k), 若b不是特征根(即m=0)
a
n
∗
=
A
b
n
a_n^*=Ab^n
an∗=Abn
例题

2.3. f(n) = b^n Pr(n) (其中Pr(n)为关于n的r次多项式,b为常数)
a
n
∗
=
n
m
b
n
Q
r
(
n
)
a_n^*=n^mb^nQ_r(n)
an∗=nmbnQr(n)
其中Qr(n) 是与Pr(n)同次的多项式,b是式(3.1.1)的m重特征根(0≤m≤k), 若b不是特征根(即m=0)
a
n
∗
=
b
n
Q
r
(
n
)
a_n^*=b^nQ_r(n)
an∗=bnQr(n)
例题

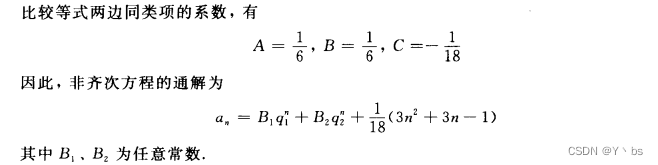
母函数方法
对于一些复杂的递推关系,利用母函数方法求解很有效,当用它求解数列{an}的递推关系时,首先作出{an}的母函数
G
(
x
)
=
∑
n
=
0
o
o
G(x)=\sum_{n=0}^{oo}
G(x)=n=0∑oo
并以他为媒介,将给定的递推关系转化为关于G(x)的方程,然后解出G(x),再将G(x)展开成x的幂级数,x^n的系数便是an
例题