文章目录
- 定义
- 转移概率 & 发射概率
- 损失函数
- 单条路径的求解
- viterbi解码
- 贪婪算法
- 维特比算法
参考解读
定义
CRF:condition random field
解决序列预测问题。比如TTS的前端分词,实体命名识别等。
转移概率 & 发射概率
-
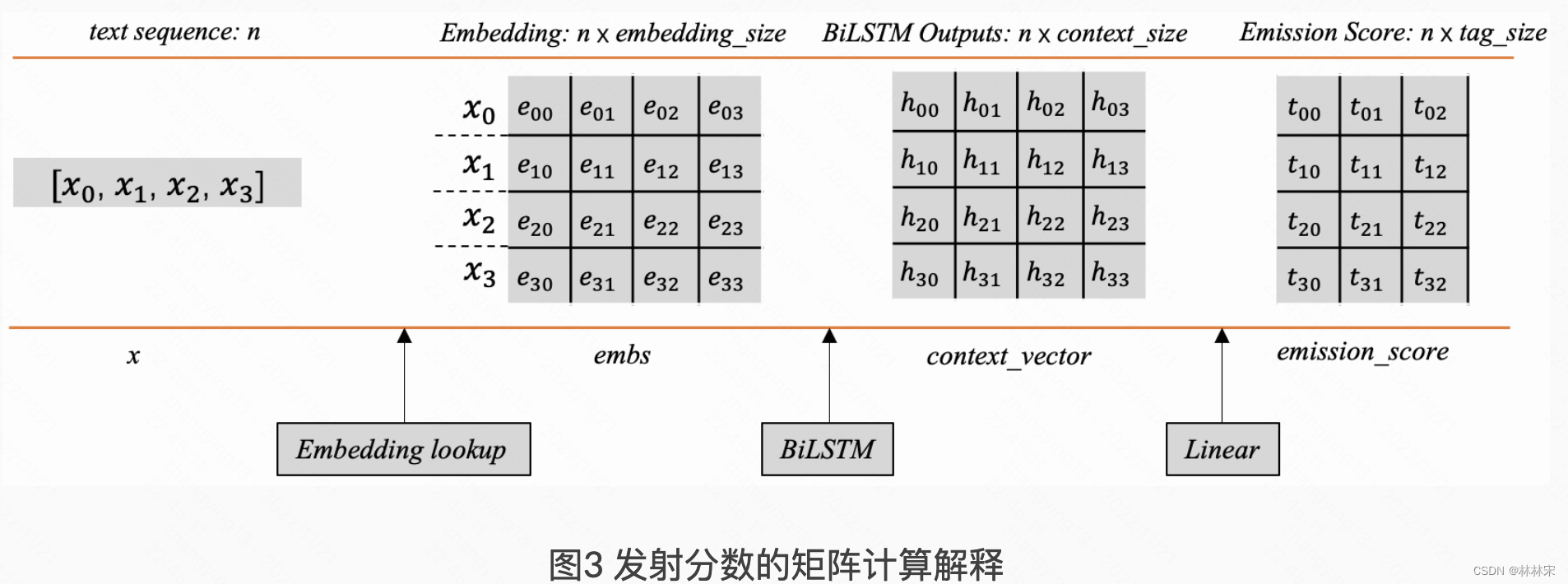
发射分数:将输入预测到不同的tag上,对应不同的分数。如下图所示, t 02 t02 t02表示输入 x 0 x_0 x0预测为tag2。
-
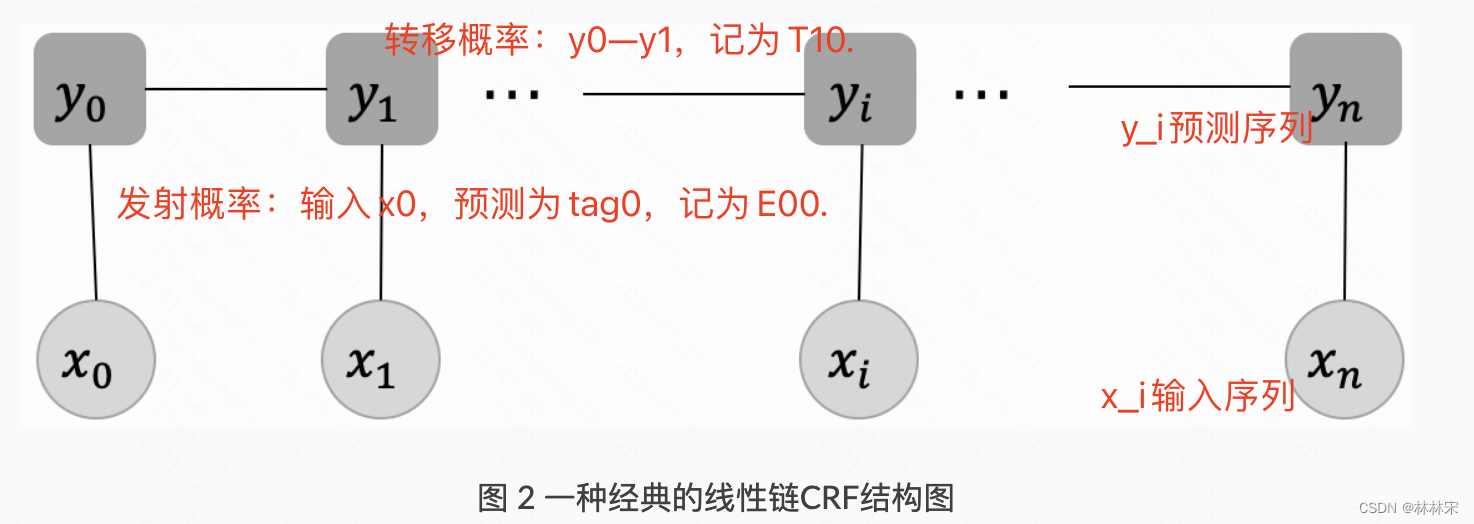
转移分数:表示一个标签向另一个标签转移的分数,分数越高,转移概率就越大。
损失函数
CRF的建模过程可以表示为
(
y
∣
x
)
=
p
(
y
n
,
.
.
.
,
y
2
,
y
1
∣
x
n
,
.
.
.
,
x
2
,
x
1
)
(y|x) = p(y_n,...,y_2,y_1|x_n,...,x_2,x_1)
(y∣x)=p(yn,...,y2,y1∣xn,...,x2,x1)
CRF的解码策略就是在所有可能的路径中,找出一条概率最大、分数最大的路径。假设标签数量是
k
k
k,文本长度为
n
n
n,则会有
N
=
k
n
N=k^n
N=kn条路径。则第
i
i
i条路径出现的概率为,其中
S
i
S_i
Si表示第
i
i
i条路径的分数。
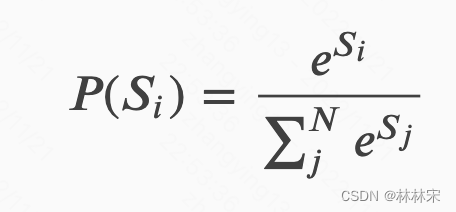
S
r
e
a
l
S_{real}
Sreal为真实最优路径的分数。对应的损失函数(
S
r
e
a
l
S_{real}
Sreal越大,loss越小)
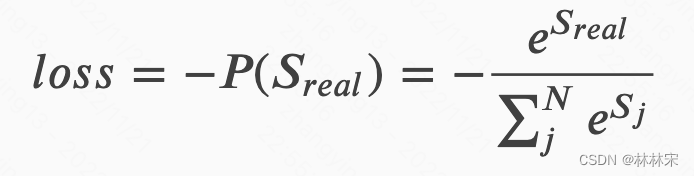
放到对数域内求解,得到
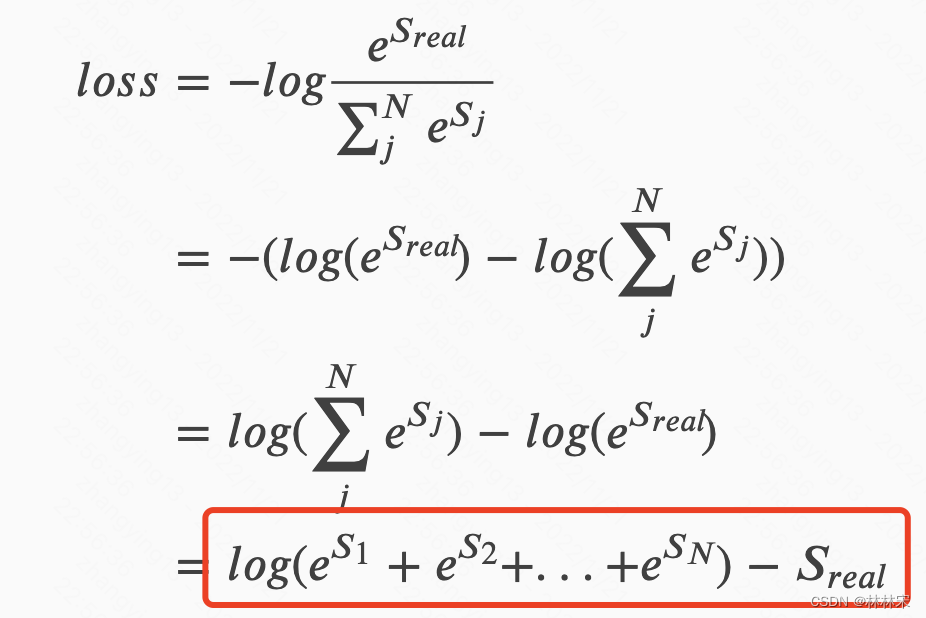
单条路径的求解
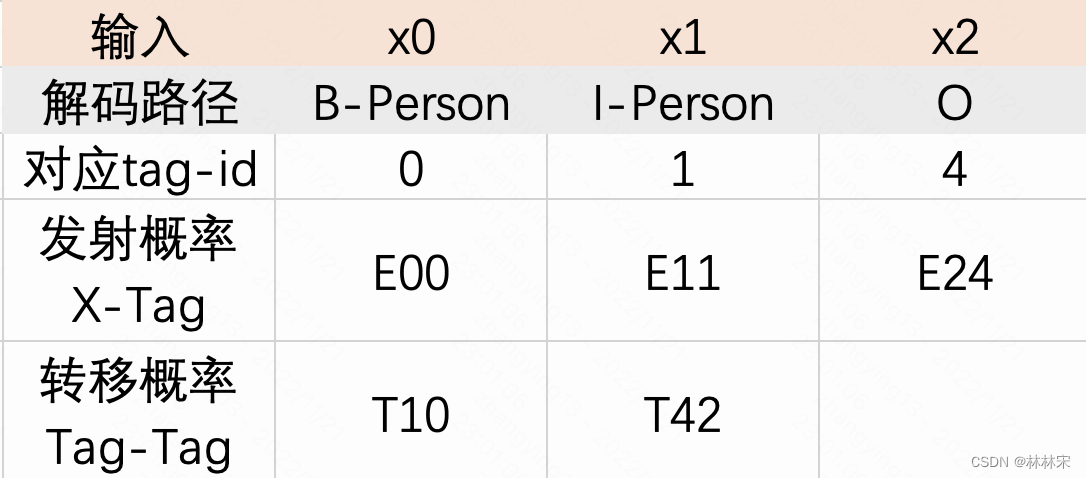
S
=
E
00
+
E
11
+
E
24
+
T
10
+
T
42
S=E_{00}+E_{11}+E_{24}+T_{10}+T_{42}
S=E00+E11+E24+T10+T42
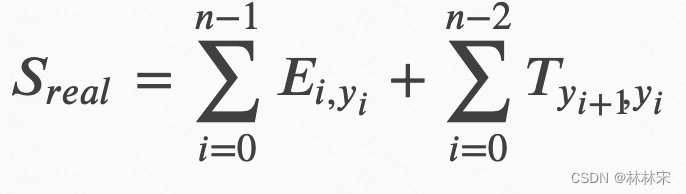
viterbi解码
最优路径算法:贪婪/集束/维特比/动态规划
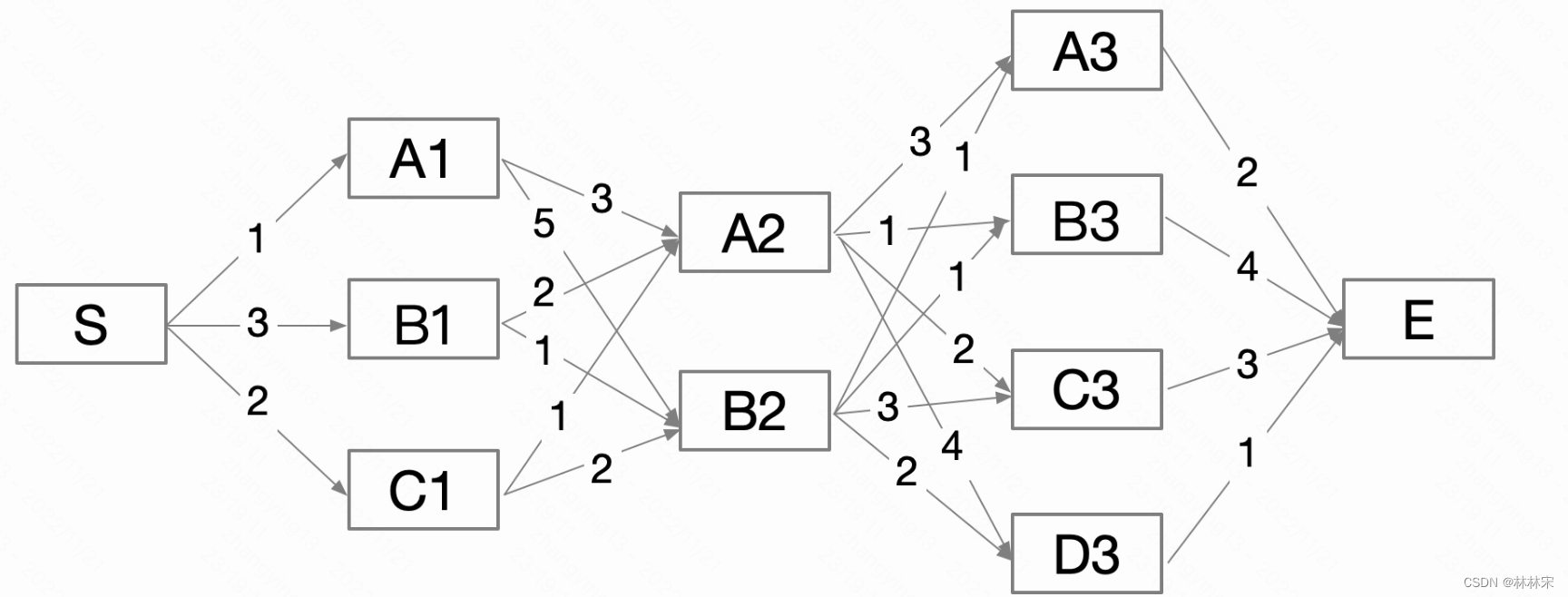
如上图所示,要找到S-E之间分数最大的路径。
贪婪算法
每一步选取最大,路径是S-B1-A2-D3-E。分数为3+2+4+1
缺点:容易陷入局部最优。
维特比算法
思路:每一步均保留到达当前每一个节点最大的路径(每个状态的最大似然)。
step1: 路径list:【S-A1, S-B1, S-C1】,sum(1,3,2)
step2: 到节点A2分数最大的路径是【S-B1-A2】=6,到节点B2分数最大的路径是【S-A1-B2】=6;
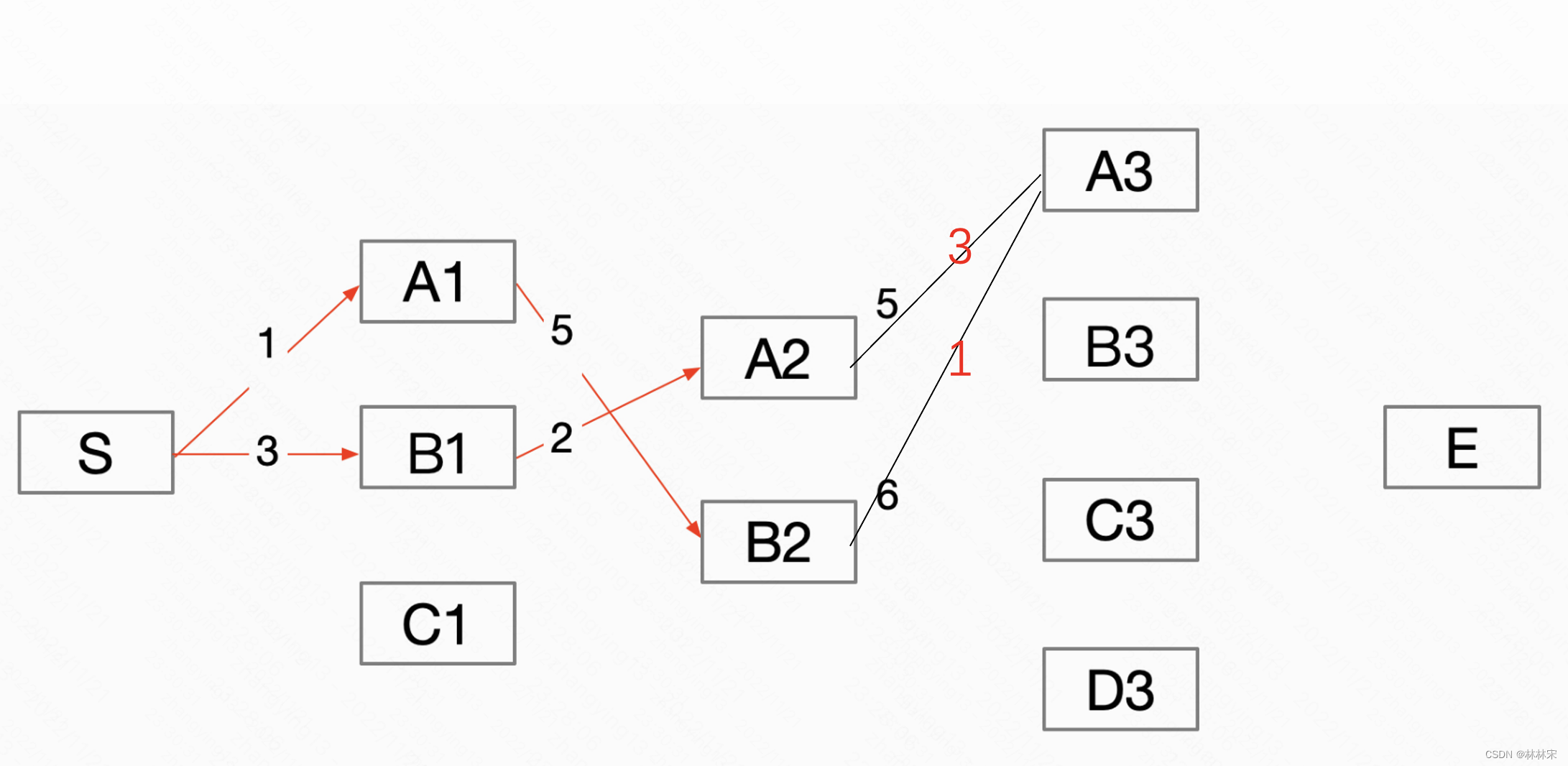
step3:到节点A3最大的路径(只能从上一步选),上一步A2的sum=3,A3_sum = Max(5+3, 6+1),因此对应的最优路径为【S-B1-A2-A3】。其他节点亦然。
最后的最优路径是
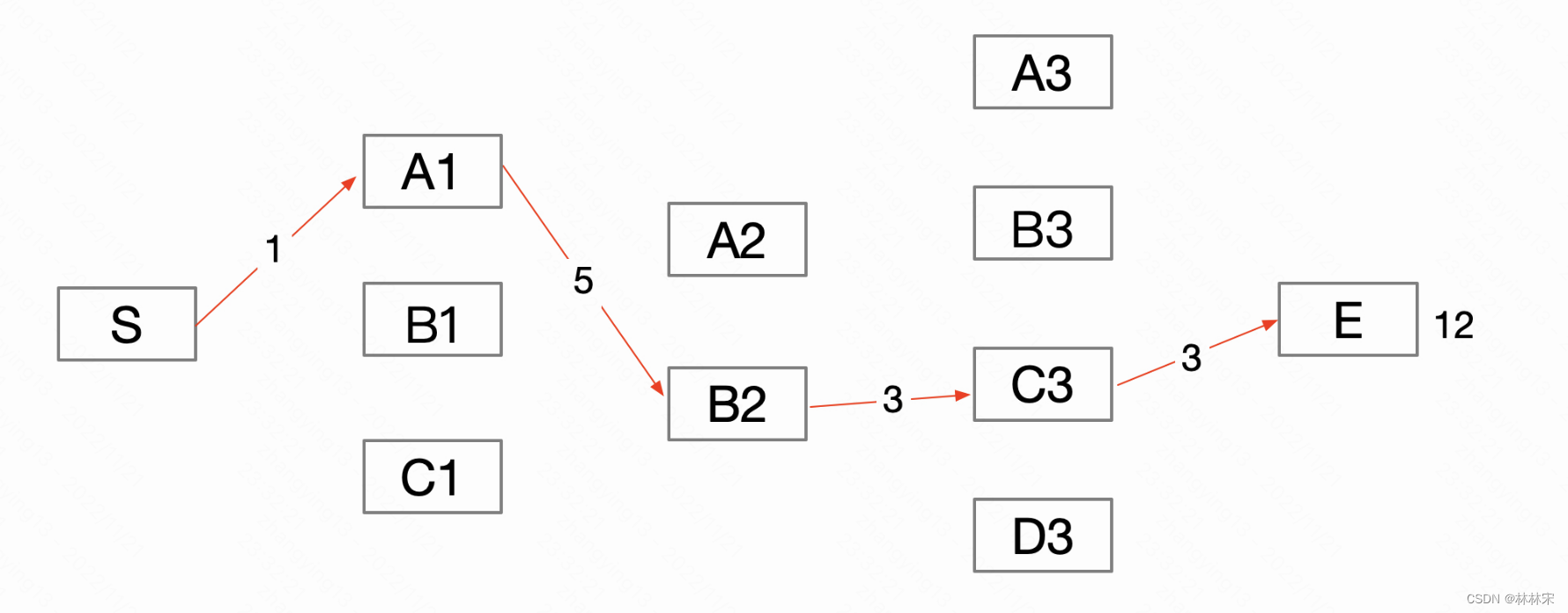
总结:维特比译码依靠这动态规划的思想,保留了每个状态的最优路径,故一定能达到全局最优。
复杂度对比:每一步有K个状态,全局路径长度为N
全局搜索:
O
(
K
N
)
O(K^N)
O(KN)
贪婪搜索:
O
(
M
+
M
+
M
.
.
.
)
=
O
(
M
∗
N
)
O(M+M+M...)=O(M*N)
O(M+M+M...)=O(M∗N)
集束搜索:
O
(
M
∗
N
∗
D
)
O(M*N*D)
O(M∗N∗D),每步选取topD
维特比搜索:
O
(
N
∗
M
2
)
O(N*M^2)
O(N∗M2)