一、前言

在之前的学习中，我们发现通过深度学习框架的高级API能够使实现线性回归变得更加容易。

同样，通过深度学习框架的高级API也能更方便地实现softmax回归模型。

本节继续使用Fashion-MNIST数据集，并保持批量大小为256。

二、实现步骤

2.1 导包

import torch
from torch import nn
from d2l import torch as d2l
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

2.2 初始化模型参数

softmax回归的输出层是一个全连接层。因此，为了实现我们的模型，我们只需在Sequential中添加一个带有10个输出的全连接层。同样，在这里Sequential并不是必要的，但它是实现深度模型的基础。我们仍然以均值0和标准差0.01随机初始化权重。

net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights)

2.3 重新审视Softmax的实现

我们计算了模型的输出，然后将此输出送入交叉熵损失。从数学上讲，这是一件完全合理的事情。然而，从计算角度来看，指数可能会造成数值稳定性问题。

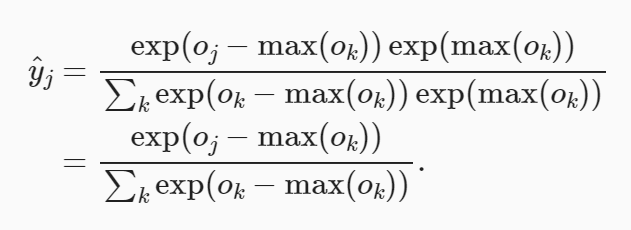
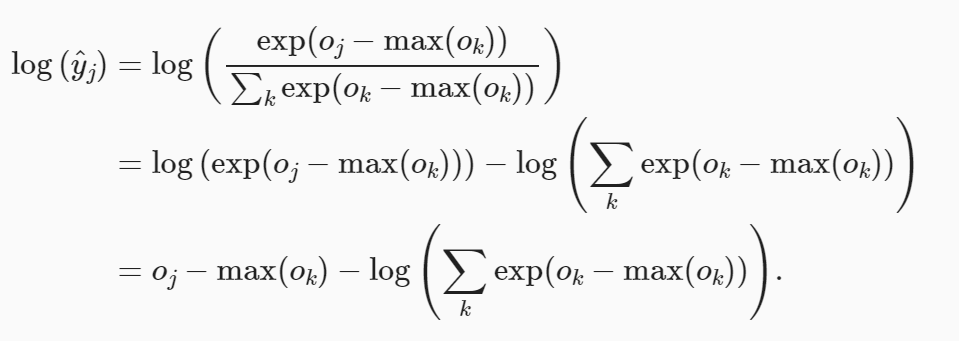
在这里插入图片描述

我们也希望保留传统的softmax函数，以备我们需要评估通过模型输出的概率。但是，我们没有将softmax概率传递到损失函数中，而是在交叉熵损失函数中传递未规范化的预测，并同时计算softmax及其对数，这是一种类似”LogSumExp技巧”的聪明方式。

loss = nn.CrossEntropyLoss(reduction='none')

2.4 优化算法

在这里，我们使用学习率为0.1的小批量随机梯度下降作为优化算法。这与我们在线性回归例子中的相同，这说明了优化器的普适性。

trainer = torch.optim.SGD(net.parameters(), lr=0.1)

2.5 训练

接下来我们调用上一节中定义的训练函数来训练模型：

num_epochs = 10
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

2.6 源代码

import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)


net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights)

loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=0.1)

num_epochs = 10
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

三、问题出现

我们根据上面的过程，尝试运行，结果出现报错：

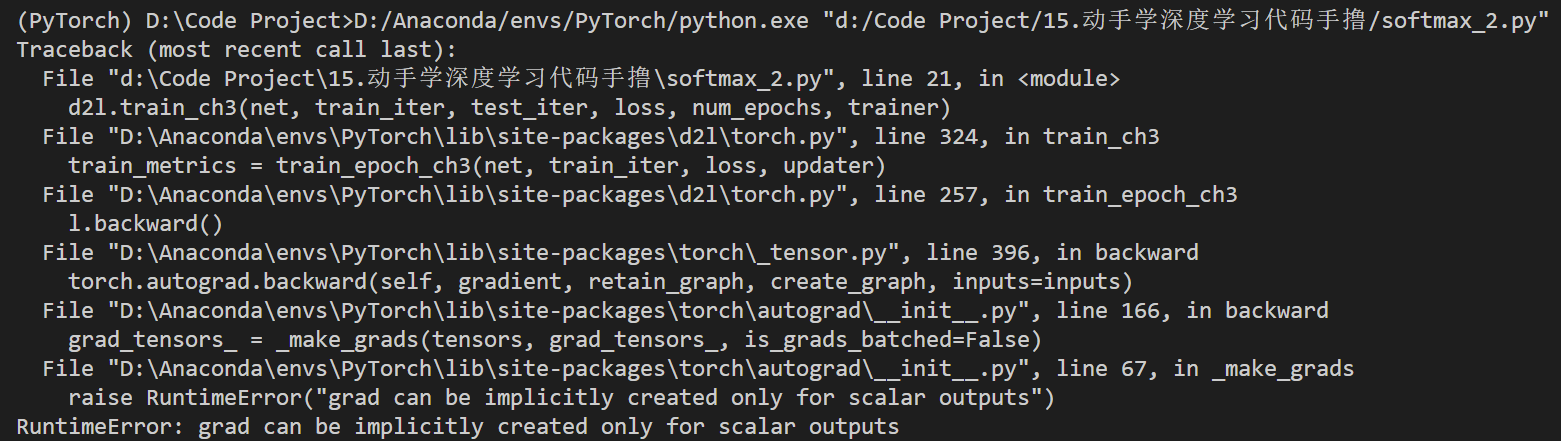
在这里插入图片描述

Traceback (most recent call last):
  File "d:\Code Project\15.动手学深度学习代码手撸\softmax_2.py", line 21, in <module>
    d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
  File "D:\Anaconda\envs\PyTorch\lib\site-packages\d2l\torch.py", line 324, in train_ch3
    train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
  File "D:\Anaconda\envs\PyTorch\lib\site-packages\d2l\torch.py", line 257, in train_epoch_ch3
    l.backward()
  File "D:\Anaconda\envs\PyTorch\lib\site-packages\torch\_tensor.py", line 396, in backward
    torch.autograd.backward(self, gradient, retain_graph, create_graph, inputs=inputs)
  File "D:\Anaconda\envs\PyTorch\lib\site-packages\torch\autograd\__init__.py", line 166, in backward
    grad_tensors_ = _make_grads(tensors, grad_tensors_, is_grads_batched=False)
  File "D:\Anaconda\envs\PyTorch\lib\site-packages\torch\autograd\__init__.py", line 67, in _make_grads
    raise RuntimeError("grad can be implicitly created only for scalar outputs")
RuntimeError: grad can be implicitly created only for scalar outputs

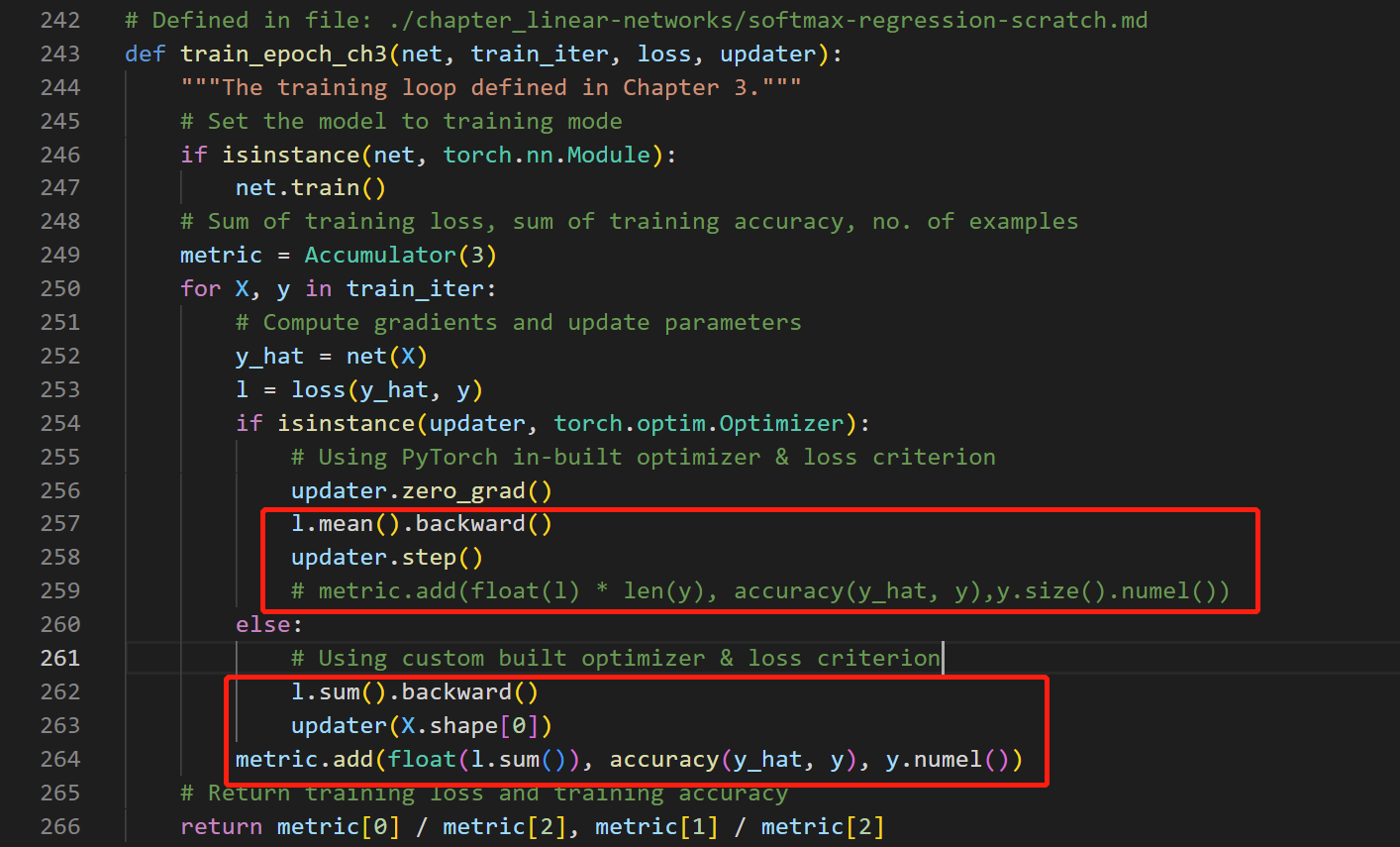
四、问题的解决

对源码进行修改：

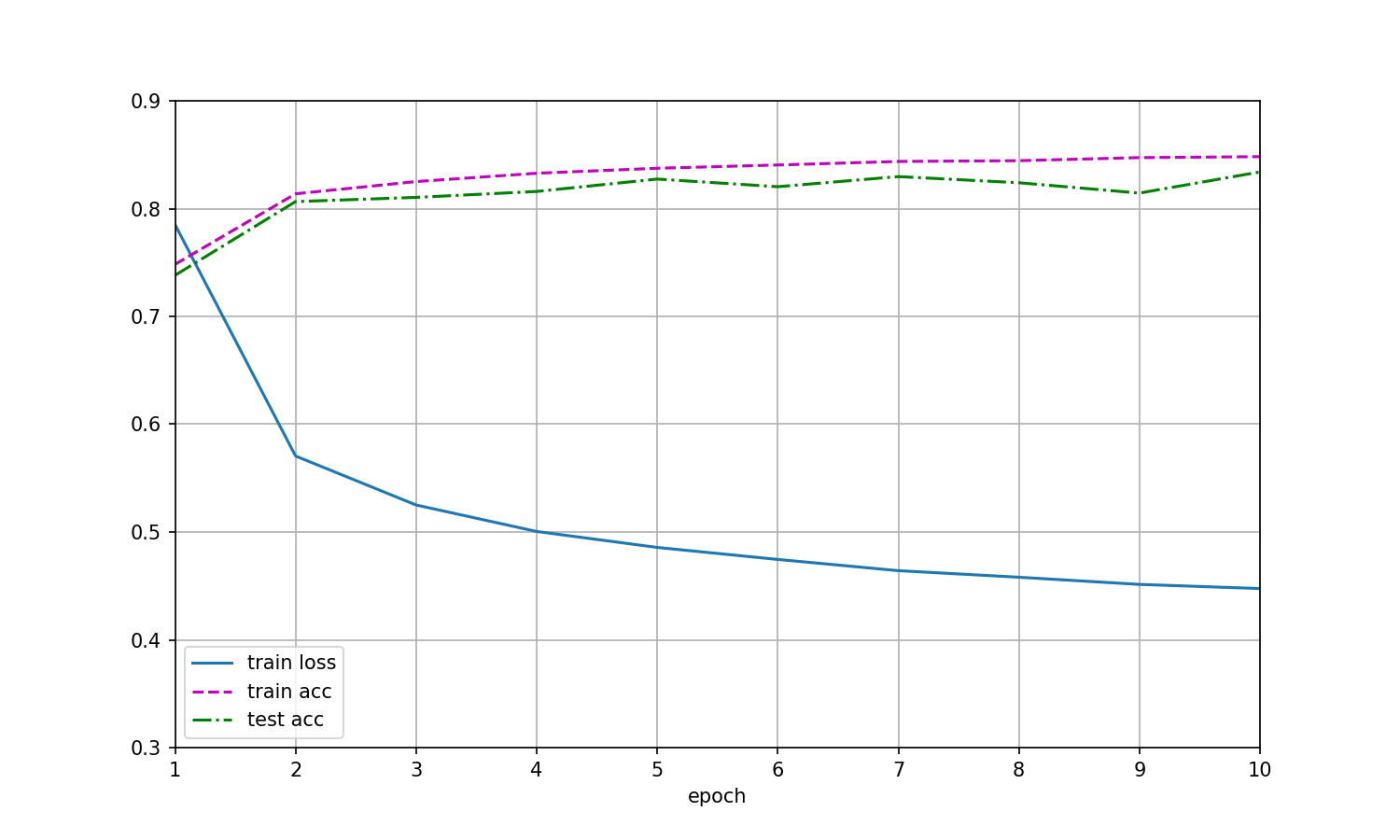
在这里插入图片描述

五、再跑代码

在这里插入图片描述
依旧是以动图的形式展示！

(PyTorch) D:\Code Project>D:/Anaconda/envs/PyTorch/python.exe "d:/Code Project/15.动手学深度学习代码手撸/softmax_2.py"
<Figure size 1500x900 with 1 Axes>
<Figure size 1500x900 with 1 Axes>
<Figure size 1500x900 with 1 Axes>
<Figure size 1500x900 with 1 Axes>
<Figure size 1500x900 with 1 Axes>
<Figure size 1500x900 with 1 Axes>
<Figure size 1500x900 with 1 Axes>
<Figure size 1500x900 with 1 Axes>
<Figure size 1500x900 with 1 Axes>
<Figure size 1500x900 with 1 Axes>

六、改正后的函数源代码

def train_epoch_ch3(net, train_iter, loss, updater):
    """The training loop defined in Chapter 3."""
    # Set the model to training mode
    if isinstance(net, torch.nn.Module):
        net.train()
    # Sum of training loss, sum of training accuracy, no. of examples
    metric = Accumulator(3)
    for X, y in train_iter:
        # Compute gradients and update parameters
        y_hat = net(X)
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer):
            # Using PyTorch in-built optimizer & loss criterion
            updater.zero_grad()
            l.mean().backward()
            updater.step()
            # metric.add(float(l) * len(y), accuracy(y_hat, y),y.size().numel())
        else:
            # Using custom built optimizer & loss criterion
            l.sum().backward()
            updater(X.shape[0])
        metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
    # Return training loss and training accuracy
    return metric[0] / metric[2], metric[1] / metric[2]