题目描述

给定一个长度为 $N$ 的数组，数组中的第 $i$ 个数字表示一个给定股票在第 $i$ 天的价格。

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

• 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
• 卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

输入格式
第一行包含整数 $N$，表示数组长度。

第二行包含 $N$ 个不超过 $10000$ 的正整数，表示完整的数组。

输出格式
输出一个整数，表示最大利润。

数据范围
$1\le N\le 10^5$

输入样例：

5
1 2 3 0 2

输出样例：

3

样例解释
对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]，第一笔交易可得利润 2-1 = 1，第二笔交易可得利润 2-0 = 2，共得利润 1+2 = 3。

---

相比于前面的股票买卖，多了一个 “冷却期” 的概念，而把它意思转换一下就是 “手中无股的第1天” ，所以需要再列出一个状态来与表示“手中无股的第2≥天”的状态区分开，因此状态机模型如下：

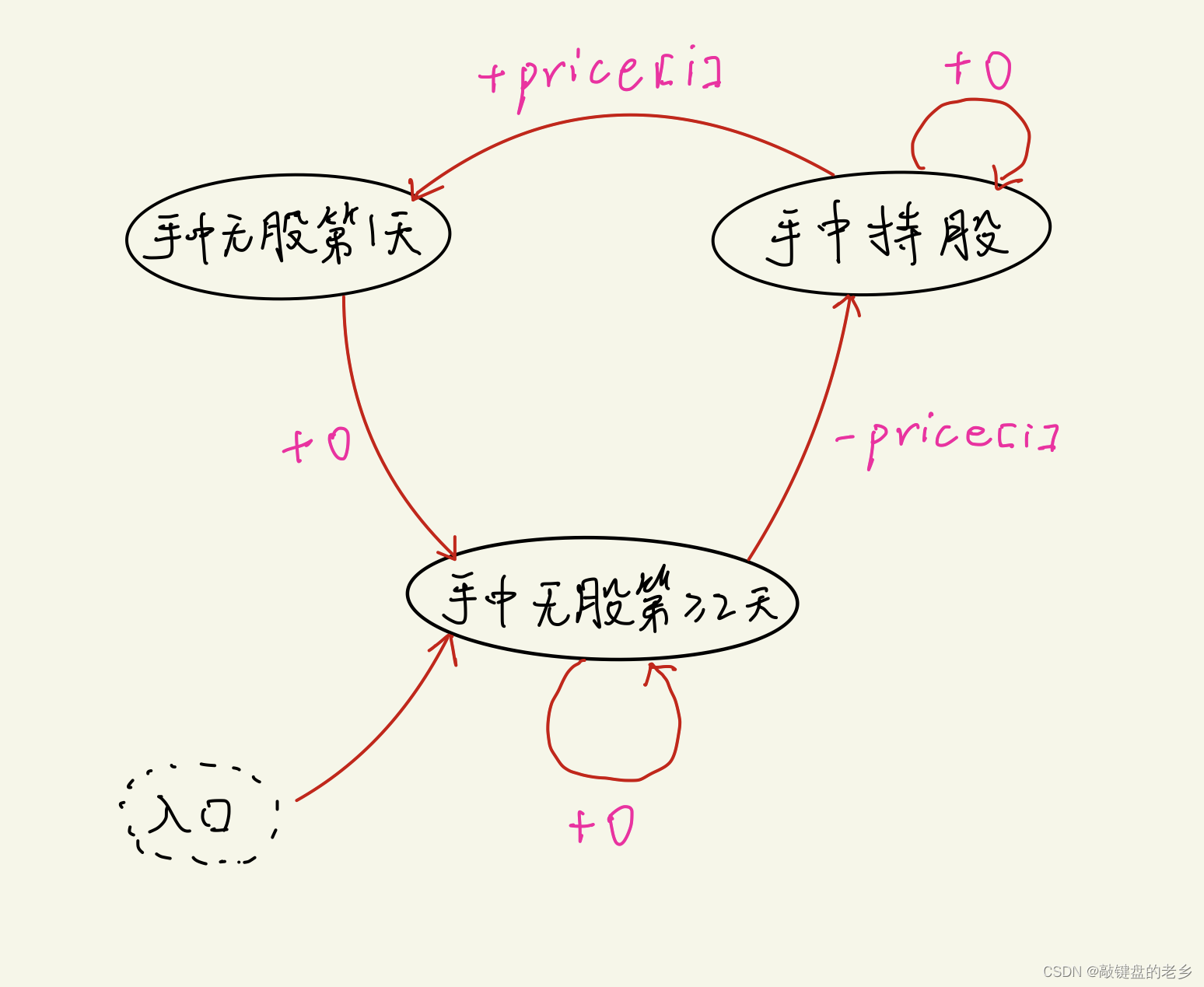
这里入口选择“手中无股第≥2天”的原因是在该状态下，既没开始买股票（笔数=0），又由于没处在冷却期，所以此时也可以开始进行买股票。

状态表示：$f(i,0/1/2)$：在第 $i$ 天时股票处于[0：手中未持股的第1天、1：手中持股、2：手中未持股的第≥2天]状态下的最大利润。
具体状态转移方程见Code。

C++代码

#include <iostream>
#include <cstring>
using namespace std;

const int N = 1e5 + 10;

int p[N];
int f[N][3];            //0：手中未持股的第1天、1：手中持股、2：手中未持股的第≥2天.
int n;

int main(){
    cin >> n;
    for(int i = 1;i <= n;i ++)      cin >> p[i];
    
    //入口是手中未持股≥2天
    memset(f, -0x3f, sizeof f);         //遇到数据量较大一点的话-∞要设置成-0x3f3f3f3f
    f[0][2] = 0;
    
    for(int i = 1;i <= n;i ++){
        f[i][0] = f[i - 1][1] + p[i];
        f[i][1] = max(f[i - 1][1], f[i - 1][2] - p[i]);
        f[i][2] = max(f[i - 1][2], f[i - 1][0]);
    }
    
    cout << max(f[n][0], f[n][2]) << endl;
    
    return 0;
}