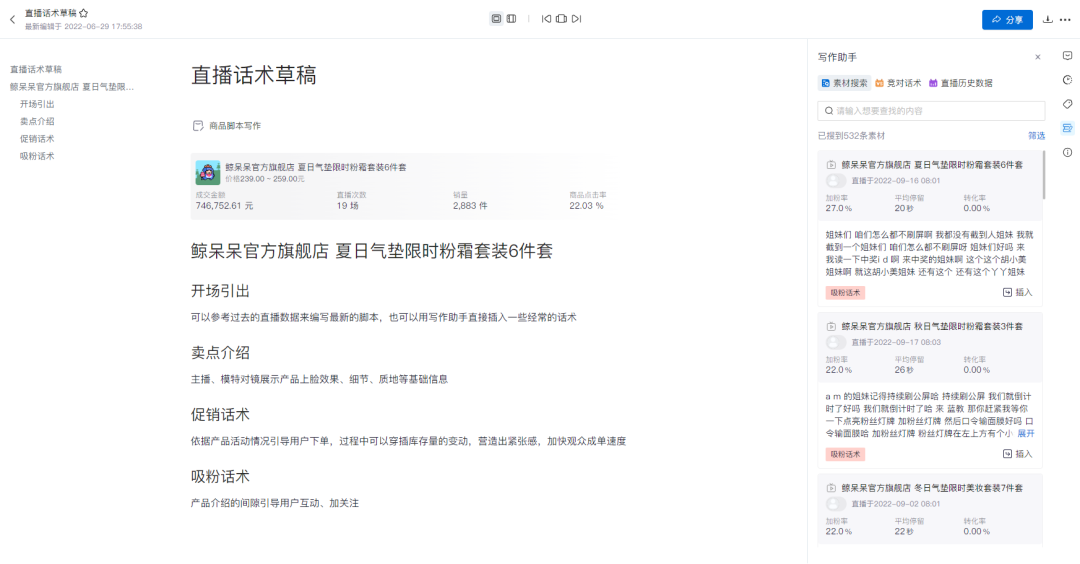
数据结构:堆
- 堆
- 1.堆是什么?
- 2.堆的特性。
- 3.堆的操作原理
- ①堆的插入原理
- ②堆的删除原理
堆
1.堆是什么?
堆是特殊的队列,不同于普通队列,从堆中取出元素是依照元素的优先级大小,而不是元素进入队列的先后顺序,也可以称堆为“优先队列”。
2.堆的特性。
特性①:用数组表示完全二叉树。
堆最常用完全二叉树来表示,因为高为h的完全二叉树有2h-1到2h-1个节点,且节点分布十分规律,也正因如此,可以用数组来实现堆的存储。
如何用数组表示完全二叉树:
- 根节点存放在数组起始处,为方便子节点找到父节点,起始处下标为1
- 找寻父节点:某节点下标为 i ,其父节点下标就为 i / 2。
- 找寻子节点:某节点下标为 i ,其左、右子节点下标分别为 2i ,2i+1。
特性②:部分有序性
任意节点元素的值与其子节点元素的值相关,相关性的不同就决定了两种不同的基本堆:最大堆 和 最小堆。
最大堆:任意节点的值大于或等于其子节点的值,根节点最大。
最小堆:任意节点的值小于或等于其子节点的值,根节点最小。
最大堆( a ),最小堆( b ) 示例:

3.堆的操作原理
(以最大堆为例)
①堆的插入原理
向最大堆插入新元素后,需要保证的是:
—堆依旧是一颗完全二叉树;
—堆中各节点与其子节点的关系依旧符合最大堆性质。
首先,在数组末尾插入新元素,若新节点值 <= 父节点值,说明位于正确位置。

在数组末尾插入新元素时,若新节点值 > 父节点值,需要交换位置,直到比父节点小或没有父节点(抵达根节点),才是抵达正确位置。

②堆的删除原理
删除元素实际上就是取出根节点的最大值元素,再删除一个节点。删除元素后,需要保证的是:
—堆依旧是一颗完全二叉树;
—堆中各节点与其子节点的关系依旧符合最大堆性质。
首先,将根节点(最大值元素)与最后一个节点交换位置,删除最后一个节点,实现取出最大值元素的操作,再删除节点的操作。
(实际上删除的节点元素在数组中依旧存在,但是代表最大堆所含节点数的MaxHeap会减去1,代表删除了最后一个节点)

完成删除操作后,需要在根节点的左、右子结点中取较大的一个与根节点做比较,根节点小于子节点则与其交换位置。
交换后,继续让此节点重复进行比较,直到此节点的值大于>=子节点值或节点成为叶子节点(不存在子节点)就停止。











![[carla入门教程]-1 安装carla环境](https://img-blog.csdnimg.cn/e2786b708614436782c033adcb0486c6.png)