摘要

基于势能的奖励塑形已被证明是提高强化学习agent收敛速度的有效方法。 这是一种以原则性方式将背景知识纳入时间差分学习的灵活技术。然而，问题仍然是如何计算用于塑形给予学习agent的奖励的势能。在本文中，我们提出了一种通过状态空间离散化来解决强化学习中这个问题的方法。特别是，我们表明可以在实际强化学习过程中并行在线学习势能函数。 如果为由给定网格确定的状态学习 $Q$ 函数，则可以并行学习具有较低分辨率（lower resolution）状态的 $V$ 函数，并用于近似地面学习的势能。 提出了新算法并进行了实验评估。

1. Introduction

------强化学习 (RL) 是一种流行的方法，用于设计从与环境的交互中学习的自主agent。与监督学习相比，RL 方法不依赖于指导性反馈，即，agent不知道在给定情况下的最佳行动是什么。相反，agent人受即时数字奖励的指导，该奖励定义了解决任务的最佳行为。这导致了两类问题：1） 时间信用分配问题，即确定动作的哪一部分值得奖励的问题；2) 收敛速度较慢：传统的 RL 算法采用延迟方法以折扣方式传播最终目标奖励或为非目标状态分配成本。然而，奖励在状态空间上的反向传播非常耗时。

------为了加快学习过程并解决时间信用分配问题，该领域已经考虑了塑形奖励的概念[1,2]。 奖励塑形的想法是给agent额外的（数字）反馈，以提高其收敛速度。

------尽管奖励塑形在许多实验中都很强大，但很快发现，如果使用不当，它也可能会产生误导 [2]。为了解决此类问题，提出了基于势能的奖励塑形 $F(s,s^{\prime })$ [1]，作为在源和目标状态 $s^{\prime }$ 上定义的一些势能函数 $\Phi$ 的差异：

------其中 γ 是贴现因子。Ng等人[1]证明，以这种方式定义的奖励塑形对于学习一种与没有奖励塑形的学习策略等效的策略是必要的，也是足够的。

------奖励塑形的一个问题是，通常无法获得关于状态势能的详细知识，或者很难以塑形奖励的形式直接表示。

------在本文中，我们提出了一种在线学习塑形奖励的方法，并用它来增强基本的强化学习。 该算法在没有任何先验知识的情况下开始，同时学习策略和塑形奖励。在每一步，塑形奖励的当前近似值用于指导目标 RL 的学习过程。该算法在两个状态空间上运行。第一个是学习地面(ground) RL 的价值函数。第二个是通过聚合(aggregating)来自地面的状态而获得的。该状态空间具有更高的概括性，用于近似塑形奖励的势能。我们研究了使用网格离散化来形成离散状态空间的情况。具有不同分辨率的两种类型的离散化自然允许形成两个状态空间：基态及其聚合(ground states and their aggregation)。

------将我们的方法与自动塑形 [3] 联系起来时，本文的贡献有两个方面：1）我们的算法通过高级强化学习在线学习奖励塑形； 2) 当可以应用状态聚合来形成抽象状态空间时，我们介绍了这种方法在 RL 中的应用。 特别是，我们研究了将连续状态空间离散化以形成可以轻松获得状态聚合的离散网格的情况。 论文的最后部分收集了相关研究的综述。

------我们的方法的主要优点是收敛速度更好此外，开销计算成本低，解决方案具有普遍适用性，知识易于获取和整合。具体来说，获得地面 RL 的离散状态所必需的知识足以应用我们的扩展。

2. Markov Decision Processes and Reinforcement Learning

------马尔可夫决策过程（MDP）是一个元组$<S，A，T，R>$，其中$S$是状态空间，$A$是动作空间，$T(s,a,s^{\prime })$是动作a在状态s中执行时将导致状态s’的概率，$R(s,a,s^{\prime })$是在状态s的动作a导致向状态s’过渡时收到的即时奖励。解决 MDP 的问题是找到一个最大化累积奖励的策略（即从状态到动作的映射）。当环境动态（转换概率和奖励函数可用）时，该任务成为一个规划问题，可以使用策略和价值迭代等迭代方法来解决[4]。

------MDP 代表 RL agent的建模框架，其目标是在环境动态不可用时学习最佳策略。因此，不能使用值迭代。然而，迭代方法本身的概念是大多数 RL 算法的支柱。这些算法应用所谓的时间差分更新来传播有关状态值 $V(s)$ 或状态-动作对 $Q(s,a)$ 的信息。这些更新基于对特定状态或状态动作值的两个时间上不同估计的差异。无模型 SARSA 就是这样一种方法[4]。它通过公式更新状态-动作值

------它修改了在状态 $s$ 中采取动作 $a$ 的值，当执行此动作后环境返回奖励 $r$，移动到新状态 $s^{\prime }$，并在状态$s^{\prime }$ 中选择动作 $a^{\prime }$。

------式（2）给出的更新规则中的即时奖励r表示来自环境的反馈。奖励塑形的想法是提供额外的奖励，这将提高agent的绩效。这个概念可以用 SARSA 算法的以下公式表示：

------其中 $F(s,a,s^{\prime })$是塑形奖励的一般形式，在我们的分析中是函数 $F:S\times S\to \mathbb{R}$。本文的主要重点是如何在特定情况下在线近似此值，当它被定义为连续状态 $s$ 和 $s^{\prime }$ 的势能差时。（见等式1。这就归结为如何学习势能$Ф(s)$的问题。值得注意的是，理想的势能等于价值函数，即$Ф(s)=V(s)$，这有助于证明为什么粗略近似价值函数是一种有前途的奖励塑形方法。

3. State Aggregation

------状态聚合( State Aggregation)代表了解决顺序决策中出现的状态空间爆炸的一种选择，特别是当环境的数学模型需要具有马尔可夫属性时 [5]。它基于将原始 MDP 的状态聚合到集群中，并将这些集群视为新 MDP 的状态。这样的 MDP 可以更容易地解决，因为它的状态空间可以显着减少。真实 MDP 的状态根据给定的相似性概念进行分组，并且在理想情况下，一个集群内的状态在策略方面应该是不可区分的（例如，处于相同抽象状态的所有状态都具有相同的最佳动作）。当聚合中的状态在这个意义上是可区分的时，这种聚合是近似的。事实上，属于一个集群的状态在多大程度上不同，决定了近似表示的质量。需要考虑求解 MDP 的高质量近似和易处理性之间的权衡。在本文中，我们提出了一种RL架构，其中原始RL问题可以以期望的精度表示（即，算法可以达到最优解，而高级近似（即使质量很低）可以提高地面学习的收敛性。

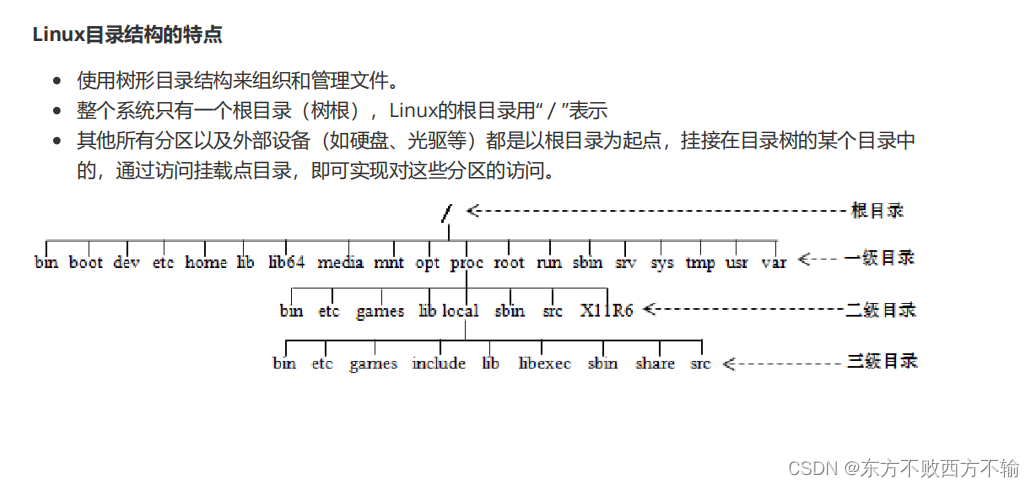
------在本文中，我们研究了当连续状态空间被离散化以形成离散状态空间时的特殊情况，其值函数可以以表格形式表示。通过应用更大间隔的离散化，可以很容易地获得用于高级学习的状态聚合（见图 1）。低级离散状态用于学习原始问题的实际解决方案，并且通过粗略近似学习抽象状态提供了有用的指导。

4. Learning Potential for Reward Shaping

------我们提出了一种具有两种不同状态空间离散化的 RL 架构。第一个是在地面 RL 级别学习 $Q$ 函数的近似值。第二个具有较低分辨率的是表示一个抽象的 $V$ 函数，该函数用作计算地面的塑形奖励（见等式 1）的势能。此处提出的算法基于该领域现有的两种技术：1) 与 MDP [6] 一起使用的多重网格离散化，以及 2) 最近提出的自动塑形 [3]。

------MDP 设置中的多重网格离散化 [6] 用于以粗到细的方式求解 MDP。虽然这种技术非常适合动态规划方法，（可以解决一个粗略的问题并将其用作更精细网格上解决方案的起点），但在应用于 RL 算法时并没有简单的方法来合并具有不同分辨率的层。第一次这样的尝试是在 [7] 中进行的，这个问题在那里很明显。在他们的解决方案中，需要了解状态空间的拓扑结构以定义多个级别是如何相关的，但这一事实使得这种方法对于 RL 任务不可行。 它使用多重网格作为获取知识的一种方式，但缺少在地面 RL 级别使用这些知识的机制。 我们提出基于势能的奖励塑形作为这些问题的解决方案。需要修改地面 RL 算法，并且可以通过额外的塑形奖励以透明的方式提供知识。

------在自动塑形方法 [3] 中，制定并求解了一个抽象的 MDP。在学习的初始阶段，建立抽象 MDP 模型，在定义的 episode 之后，精确求解抽象 MDP，并将其值函数用作基态的势能。在本文中，我们提出了一种算法，该算法在连续状态空间离散化以表格形式表示时应用多重网格策略。我们没有将抽象任务定义为解决抽象 MDP 的动态规划，而是使用 RL 在线解决高级任务。因为这种抽象的 RL 不需要学习模型，所以可以从学习开始就提供塑形奖励。此外，多重网格离散化会在基础层和抽象层之间产生自然转换。我们的方法不需要比在地面定义离散化所需的更多的环境知识。我们不需要将抽象转换为基态或近似环境动力学（抽象级别的转换概率）的方法。

------算法 1 总结了我们的方法。 它遵循 4 中的 SARSA 结构。在我们的案例中，底层学习与基线学习相同。修改是在算法 1 的第 16 行中为基本 SARSA 提供塑形奖励 $F(s,s^{\prime })$ 的点，其中计算了基态的时间差异。$F(s,s^{\prime })$ 的计算方式定义了我们的扩展。

------塑形奖励 $F(s,s^{\prime })$ 在第 13 行计算为agent访问的当前和先前状态的价值函数的差异。因此 $Ф(s)=V(z)$，其中 $V(z)$ 是抽象级别的值函数，状态 $s$ 由给定状态$z$ 聚合。使用时间差分更新（第 9 行）学习值 $V(z)$。所有与该任务相关的参数在算法中都有下标$v$。从状态$s$到相应状态 $z$ 的映射以直接的方式完成，无需任何特殊知识。基本上，抽象状态$z$聚合基态$s$和包容可以很容易地确定。然而，通过可选的、关于问题的额外知识，这样的映射可以删除抽象表示中的一些状态变量，并适当地关注高级学习。

------高级 RL 被视为半 MDP [8]，因为由于更高的泛化，agent可以在一个高级位置中执行多个时间步骤。因此，当计算第 9 行中的时间差时使用时间 $t$。

------通用函数 $rewar{d}_v(r)$ 表明高级学习可以获得内部修改的奖励。在定义此功能时可能要考虑的事实是，塑形奖励不应掩盖环境的奖励提供者，因为它可能会导致次优解决方案，例如，该势能基于不可接纳的启发式。