先看一道题目:
从键盘获取一个正整数,如果把它转为16进制的数字,那么它是一个几位数呢?如果把它转为28进制又是一个几位数呢?
在讲这个题目之前,我们先要了解进制转换
什么是进制转换?
简单来说,进制就是数位的表示方法。
十进制(常用)是每逢10进1。
二进制是每逢2进1。
八进制是每逢8进1。
十六进制是每逢16进1。
而进制转换,就是把一个数从一种进制换到另一种进制表示。
比如:
十进制 10 转成二进制 = 1010
十进制 10 转成八进制 = 12
十进制 10 转成十六进制 = A
虽然数字代表的大小不变,但写法变了!
怎么进行进制转换?(超简单版)
1. 十进制 → 其他进制
方法:不断除目标进制,记录余数,最后倒着读。
比如:
十进制123转成8进制
123 ÷ 8 = 15 余 3
15 ÷ 8 = 1 余 7
1 ÷ 8 = 0 余 1
余数倒着读:1 7 3 → 八进制是173
2. 其他进制 → 十进制
方法:按照位数乘以进制的幂次方,加起来。
比如:
八进制173转回十进制
= 1×8² + 7×8¹ + 3×8⁰ //1在百位所以是平方,7在十位所以是1次方,类比十进制
= 1×64 + 7×8 + 3×1
= 64 + 56 + 3
= 123
这道题目求进制转化后的数字的位数,其实就是求进制转化过程中除的次数!
现在直接给出这道题目的代码:
int Fun1(int x,int n)//统计x转为n进制是个几位数
{
int count = 0;//计数器
while (x != 0)
{
x /= n;
count++;
}
return count;
}
int main()
{
printf("%d\n", Fun1(123, 10));//3
printf("%d\n", Fun1(123, 16));//2
printf("%d\n", Fun1(123, 8));//3
printf("%d\n", Fun1(123, 2));//7
printf("%d\n", Fun1(123, 28));
return 0;
}首先,看看函数 Fun1:
int Fun1(int x,int n)//统计x转为n进制是个几位数
{
int count = 0;//计数器
while (x != 0)
{
x /= n;
count++;
}
return count;
}
简单理解就是:
把数字 x 按 n 进制去表示,看看一共需要多少位。
每次 x /= n,就相当于“去掉”一位。
直到 x 变成0,统计了一共去过几次,就是它的位数。
再看 main 函数:
int main()
{
printf("%d\n", Fun1(123, 10));//3
printf("%d\n", Fun1(123, 16));//2
printf("%d\n", Fun1(123, 8));//3
printf("%d\n", Fun1(123, 2));//7
printf("%d\n", Fun1(123, 28));
return 0;
}逐行解释一下输出:
Fun1(123, 10):
123是十进制本身。
123 / 10 = 12
12 / 10 = 1
1 / 10 = 0 (结束)
总共除过3次,所以是3位。
Fun1(123, 16):
123转16进制是 7B。
123 / 16 = 7
7 / 16 = 0
两次,所以是2位。
Fun1(123, 8):
123转8进制是173。
123 / 8 = 15
15 / 8 = 1
1 / 8 = 0
三次,所以是3位。
Fun1(123, 2):
123转二进制是1111011。
123 / 2 = 61
61 / 2 = 30
30 / 2 = 15
15 / 2 = 7
7 / 2 = 3
3 / 2 = 1
1 / 2 = 0
七次,所以是7位。
Fun1(123, 28):
123 / 28 = 4
4 / 28 = 0
两次,所以是2位。
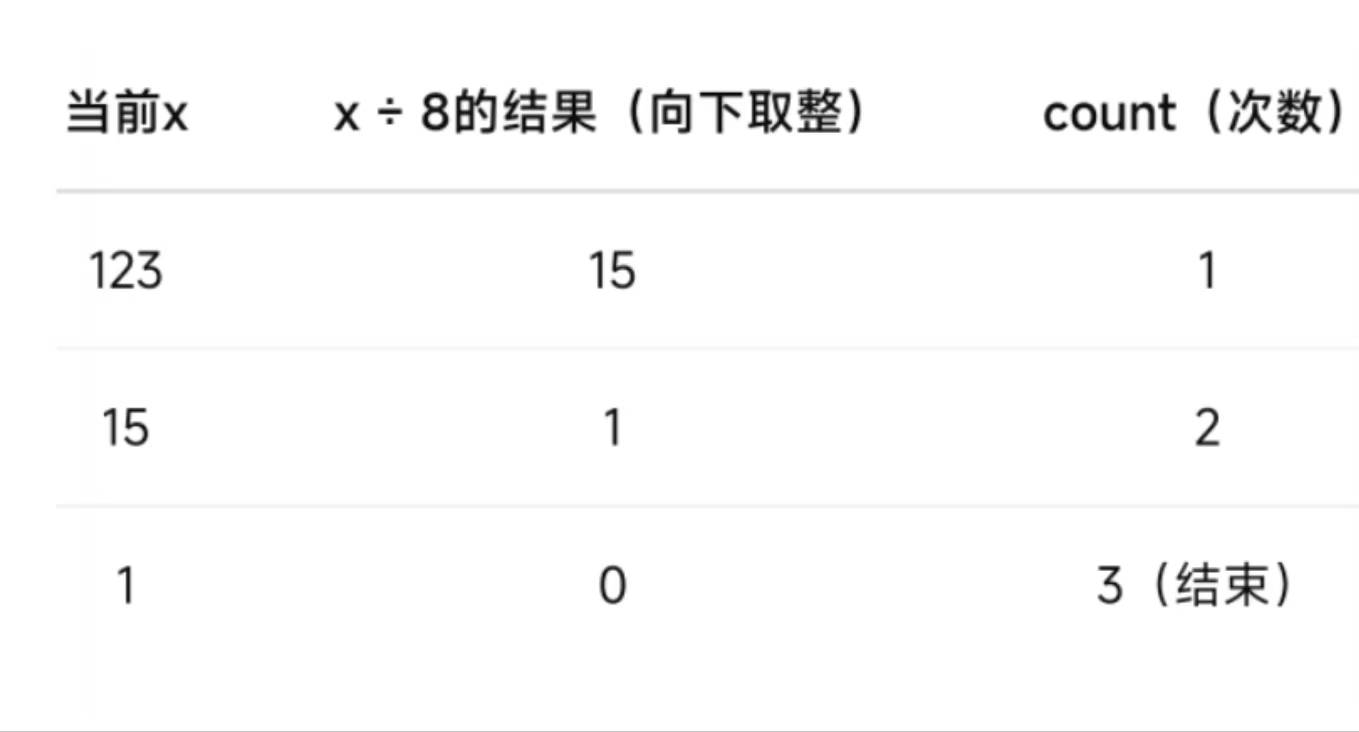
图示:以Fun1(123,8)为例
(也就是求123在8进制下是几位)
我们做的是不断除以8,来"去掉"低位:
(这道题目求进制转化后的数字的位数,其实就是求进制转化过程中除的次数!)
总结一句话:
Fun1(x, n) 实际上是 x在n进制下所需要的位数,
原理是每次除以n,把最低位"丢掉",直到剩0,统计除的次数。
再看一题:
假设在n进制下,下面的等式成立,567*456=150216,n的值是()。
A. 9 B. 10 C. 12 D.18
int main()
{
for (int n = 9; n <= 18; n++)//进制
{
if ((5 * n * n + 6 * n + 7) * (4 * n * n + 5 * n + 6) ==
((int)pow(n, 5) + 5 * (int)pow(n, 4) + 2 * n * n + n+6))
{
printf("%d\n",n);
break;
}
}
//int n = (int)pow(10,5);//(int):把后面的double强制转换为int
//printf("%d\n",n);
return 0;
}逐步解释:
for (int n = 9; n <= 18; n++)n从9开始,每次循环n++,直到n=18。
每次都检查一个条件,想找一个满足特定数学关系的n。
if ((5 * n * n + 6 * n + 7) * (4 * n * n + 5 * n + 6) ==
((int)pow(n, 5) + 5 * (int)pow(n, 4) + 2 * n * n + n+6))判断式的左边:
(5n² + 6n + 7) * (4n² + 5n + 6)
判断式的右边:
n⁵ + 5n⁴ + 2n² + n + 6
(注意:pow(n, 5)和pow(n, 4)是计算n的5次方、4次方,因为pow返回double类型,所以用(int)强制类型转换成整数。)
如果左边和右边的结果相等:
printf("%d\n", n); 输出这个n
break; 退出循环(因为已经找到了)。
整体意思总结:
在n从9到18的范围里,找一个n,使得 (5n² + 6n + 7)*(4n² + 5n + 6) 等于 n⁵ + 5n⁴ + 2n² + n + 6,并输出这个n。