2、字母异位词分组

方法一:排序+哈希表
思路:对每个字符串排序,排序后的字符串作为键插入到哈希表中,值为List<String>形式存储单词原型,键为排序后的字符串。
Map<String, List<String>> m = new HashMap<>();难点(重点):
1、排序字符串
字符串本身不能直接排序,需要先利用str.toCharArray()转换成为char[],再利用Arrays.sort(s);完成排序,但排序完的s就是char[]形式的。
2、哈希表map已有的接口computeIfAbsent(Key,Function)
map.computeIfAbsent(Key, Function)
- 若键存在:直接返回对应的值(在本题中返回的就是对应的列表)。
- 若键不存在:调用
Function生成新值(本题中就是生成一个空的列表作为新的键对应的值),将键值对存入 Map,并返回新值。这个方法的平替:但也需要知道map.getOrDefault()方法
List<String> list = map.getOrDefault(key, new ArrayList<String>()); list.add(str); map.put(key, list);值得注意的是:这个Key需要对应map的键值的类型。不能用char[]作为键的类型,因为所有数组类型(如
char[])继承自Object,其hashCode()和equals()基于对象地址(而非内容)。键可以选用基本类型和部分引用类型:
3、返回值要是List<List<String>>,
Map.values()的返回值是类型为
Collection<List<String>>的所有值(List<String>) 的集合。要返回List<List<String>>只需要新建一个ArrayList<>(map.values())即可。
class Solution {
public List<List<String>> groupAnagrams(String[] strs) {
Map<String, List<String>> m = new HashMap<>();
for (String str : strs) {
char[] s = str.toCharArray();
Arrays.sort(s);
// s 相同的字符串分到同一组
m.computeIfAbsent(new String(s), k -> new ArrayList<>()).add(str);
}
return new ArrayList<>(m.values());
}
}3、 最长连续序列
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
输入:nums = [100,4,200,1,3,2] 输出:4 解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
class Solution {
public int longestConsecutive(int[] nums) {
Arrays.sort(nums);
int ans = 1;
int n = nums.length;
if(n==0){
return 0;
}
int tmp = nums[0];
int count = 1;
for(int i = 1;i<n;i++){
if(nums[i]==tmp+1){
count++;
ans = Math.max(ans,count);
tmp = nums[i];
continue;
}else if(nums[i]==tmp){
continue;
}else{
count = 1 ;
tmp = nums[i];
ans = Math.max(ans,count);
}
}
return ans;
}
}4、移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
思路:
双指针问题——>left指针指向待填充的位置,依次加1;right指针从小到大依次指向非零的。
相当于右指针每遇到一个非零的数,就把他按照left指针依次存到数组里
class Solution {
public void moveZeroes(int[] nums) {
int n = nums.length;
if(n == 1 || n == 0){
return;
}
int l = 0;
int r = 0;
while(r<n){
if(nums[r] !=0 ){
int tmp = nums[l];
nums[l] = nums[r];
nums[r] = tmp;
r++;
l++;
}else{
r++;
}
}
}
}5、盛最多水的容器
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器
示例 1:
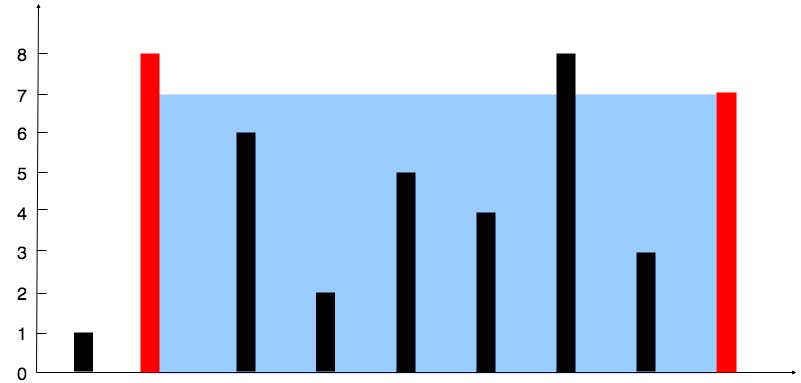
输入:[1,8,6,2,5,4,8,3,7] 输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
思路:
先框到最大,往里缩的时候,肯定是去变化那个最小的边,因为是由于那个边小面积才小的。
class Solution {
public int maxArea(int[] height) {
int l = 0;
int r = height.length-1;
int ans = 0;
while(l<r){
ans = Math.max(ans,(r-l)*Math.min(height[r],height[l]));
if(height[l]<height[r]){
l++;
}else{
r--;
}
}
return ans;
}
}6、三数之和
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
思路:
如果是有序数组,遍历第一个数,则三个数之和相当于在第一个数的右边找两个数和为-nums[i]。
值得注意的是,要避免重复,例如第一个数在遍历的时候就要判断是不是重复了;
后续如果满足了,通过ans.add(List.of(三个数));即可,然后跳过重复的字段。
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
Arrays.sort(nums);
List<List<Integer>> ans = new ArrayList<>();
int n = nums.length;
for (int i = 0; i < n - 2; i++) {
int x = nums[i];
if (i > 0 && x == nums[i - 1]) continue; // 跳过重复数字
if (x + nums[i + 1] + nums[i + 2] > 0) break; // 优化一
if (x + nums[n - 2] + nums[n - 1] < 0) continue; // 优化二
int j = i + 1;
int k = n - 1;
while (j < k) {
int s = x + nums[j] + nums[k];
if (s > 0) {
k--;
} else if (s < 0) {
j++;
} else { // 三数之和为 0
ans.add(List.of(x, nums[j], nums[k]));
//for (j++; j < k && nums[j] == nums[j - 1]; j++); // 跳过重复数字
while(++j < k && nums[j] == nums[j - 1]);
//for (k--; k > j && nums[k] == nums[k + 1]; k--); // 跳过重复数字
while(--k>j && nums[k] == nums[k+1]);
}
}
}
return ans;
}
}7、接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
思路:
接雨水经典问题:把每一个点当成一个桶,这个点能存多少水取决于他的左右两侧最高值的最小值,否则水会从两边流出去。如果左右两边的最值中相对小的数>这个桶本身的高度,则属于正常接雨水,差值就是接到的雨水。
class Solution {
public int trap(int[] height) {
int n = height.length;
int[] pre = new int[n];
int[] lst = new int[n];
pre[0] = height[0];
lst[n-1] = height[n-1];
for(int i = 1;i<n;i++){
pre[i] = Math.max(pre[i-1],height[i]);
}
for(int i = n-2 ; i>=0 ;i--){
lst[i] = Math.max(height[i],lst[i+1]);
}
int ans = 0;
for(int i = 1;i < n-1 ; i++){
int tmp = Math.min(pre[i],lst[i]);
if(tmp > height[i]){
ans+=(tmp-height[i]);
}
}
return ans;
}
}8、无重复字符的最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长 子串 的长度。
示例 1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
(1)官方得到滑动窗口(更快)
利用哈希表记录每一个字母在滑动窗口中第一次出现的位置。
关键点的是怎么更新哈希表,通过左右指针,判断右指针指向的字符是不是已经存在在哈希表中且在左指针的右边,如果是,就相当于被滑动窗口框住了,也就是说框住的字符串由于右指针的加入,出现了重复的字符,所以要更新左指针和右指针指向的字符在滑动窗口中第一次出现的位置,把左指针指向右指针的字符原本第一次出现的位置+1的位置。
class Solution {
public int lengthOfLongestSubstring(String s) {
Map<Character, Integer> map = new HashMap<>(); // 记录字符的最近一次出现位置
int ans = 0; // 最长子串长度
int left = 0; // 滑动窗口左边界
for (int right = 0; right < s.length(); right++) {
char c = s.charAt(right);
// 关键逻辑:如果字符 c 已经存在,且其位置 >= left,说明它在当前窗口内重复了
if (map.containsKey(c) && map.get(c) >= left) {
left = map.get(c) + 1; // 将左边界移动到重复字符的下一个位置
}
map.put(c, right); // 更新字符 c 的最新位置
ans = Math.max(ans, right - left + 1); // 计算当前窗口长度,更新最大值
}
return ans;
}
}(2)我的思路
利用哈希表记录每个字符出现的次数
需要一个公共参数index,判断每次新加的字符是不是已经出现过,如果已经出现过,利用while循环执行把index++指向的字符出现的次数减1,直到新加的字符出现的次数不再大于1。
class Solution {
public int lengthOfLongestSubstring(String S) {
Map<Character,Integer> map = new HashMap<>();
char[] s = S.toCharArray();
int n = s.length;
int ans = 0;
int index = 0;
for(int i = 0; i<n ; i++){
if(map.containsKey(s[i])){
map.put(s[i],map.get(s[i])+1);
}else{
map.put(s[i],1);
}
if(map.get(s[i])==1){
ans = Math.max(ans,i-index+1);
}
while(map.get(s[i])>1){
map.put(s[index],map.get(s[index])-1);
index++;
}
}
return ans;
}
}9、找到字符串中所有字母异位词
给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
示例 1:
输入: s = "cbaebabacd", p = "abc" 输出: [0,6] 解释: 起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。 起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。
(1)
标准的定长滑动窗口
关键:(1)利用 字符-‘a’ 把字符转换为数字,设 int[ ] cnt = new int[26]
(2)Arrays的一个接口方法:Arrays.equal(数组1,数组2)
(3)滑动窗口三个步骤:入——>更新——>出
class Solution {
public List<Integer> findAnagrams(String s, String p) {
List<Integer> ans = new ArrayList<>();
int[] cntP = new int[26]; // 统计 p 的每种字母的出现次数
int[] cntS = new int[26]; // 统计 s 的长为 p.length() 的子串 s' 的每种字母的出现次数
for (char c : p.toCharArray()) {
cntP[c - 'a']++; // 统计 p 的字母
}
for (int right = 0; right < s.length(); right++) {
cntS[s.charAt(right) - 'a']++; // 右端点字母进入窗口
int left = right - p.length() + 1;
if (left < 0) { // 窗口长度不足 p.length()
continue;
}
if (Arrays.equals(cntS, cntP)) { // s' 和 p 的每种字母的出现次数都相同
ans.add(left); // s' 左端点下标加入答案
}
cntS[s.charAt(left) - 'a']--; // 左端点字母离开窗口
}
return ans;
}
}(2)不定长窗口
class Solution {
public List<Integer> findAnagrams(String s, String p) {
List<Integer> ans = new ArrayList<>();
int[] cnt = new int[26]; // 统计 p 的每种字母的出现次数
for (char c : p.toCharArray()) {
cnt[c - 'a']++;
}
int left = 0;
for (int right = 0; right < s.length(); right++) {
int c = s.charAt(right) - 'a';
cnt[c]--; // 右端点字母进入窗口
while (cnt[c] < 0) { // 字母 c 太多了
cnt[s.charAt(left) - 'a']++; // 左端点字母离开窗口
left++;
}
if (right - left + 1 == p.length()) { // s' 和 p 的每种字母的出现次数都相同
ans.add(left); // s' 左端点下标加入答案
}
}
return ans;
}
}10、 和为 K 的子数组
(1)枚举
两个for循环枚举每一个数打头的可能性。
public class Solution {
public int subarraySum(int[] nums, int k) {
int count = 0;
for (int start = 0; start < nums.length; ++start) {
int sum = 0;
for (int end = start; end >= 0; --end) {
sum += nums[end];
if (sum == k) {
count++;
}
}
}
return count;
}
}
(2)前缀和优化
枚举的思想是,确定1个开头的数字nums[i],然后依次求他后面所有数的和;
前缀和的思想:
定义 pre[i] 为 [0..i] 里所有数的和,则 pre[i] 可以由 pre[i−1] 递推而来,即:
pre[i]=pre[i−1]+nums[i]。那么j到i的和就为pre[i]-pre[j-1],判断是否为k即可。
也就相当于找k+pre[j-1]是否存在
利用哈希表,把前缀和作为键,值为出现的次数。由于是按照从小到大顺序走的,所以出现的次数只会是i之前的和,所以也就相当于遍历了一遍0~i。
public class Solution {
public int subarraySum(int[] nums, int k) {
int count = 0, pre = 0;
HashMap < Integer, Integer > mp = new HashMap < > ();
mp.put(0, 1);
for (int i = 0; i < nums.length; i++) {
pre += nums[i];
if (mp.containsKey(pre - k)) {
count += mp.get(pre - k);
}
mp.put(pre, mp.getOrDefault(pre, 0) + 1);
}
return count;
}
}
要注意的是:这个key是子串和,值为个数。当pre = k时, 不管map里面有没有和为0的,肯定是满足的,所以提前存一个(0,1),处理前缀和直接等于
k的情况。
11、 滑动窗口最大值
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3 输出:[3,3,5,5,6,7] 解释: 滑动窗口的位置 最大值 --------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7
方法一:单调队列

思路:
利用单调队列求:
如果即将进入到框内的数更小,当大的走了这个小的有可能成为最大,但如果即将进来的数比末尾数大,那么这个末尾数就再也不会当做最大值,因为末尾值比即将进来的数小而且走的还早。也就相当于只在队列中保存从大到小的数(单调队列),出现小到大就扔掉小的;
当队列中人数超了,扔掉队首的数,下一个最大的只会是新队首。
主要用到的ArrayDeque<>的方法:
(1)getLast() getFirst();
(2)removeLast()
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int n = nums.length;
int[] ans = new int[n - k + 1];
Deque<Integer> q = new ArrayDeque<>(); // 双端队列
for (int i = 0; i < n; i++) {
// 1. 入
while (!q.isEmpty() && nums[q.getLast()] <= nums[i]) {
q.removeLast(); // 维护 q 的单调性
}
q.addLast(i); // 入队
// 2. 出
if (i - q.getFirst() >= k) { // 队首已经离开窗口了
q.removeFirst();
}
// 3. 记录答案
if (i >= k - 1) {
// 由于队首到队尾单调递减,所以窗口最大值就是队首
ans[i - k + 1] = nums[q.getFirst()];
}
}
return ans;
}
}
(简单看了下,还没理解)方法二 优先级队列
我们不断地移除堆顶的元素,直到其确实出现在滑动窗口中。此时,堆顶元素就是滑动窗口中的最大值。为了方便判断堆顶元素与滑动窗口的位置关系,我们可以在优先队列中存储二元组 (num,index),表示元素 num 在数组中的下标为 index。
算法步骤
-
初始化优先队列
使用自定义比较器,队列中的元素是包含数值和索引的数组。比较规则:- 数值降序:数值大的元素优先。
- 索引降序:数值相同时,索引大的元素优先。
PriorityQueue<int[]> pq = new PriorityQueue<>(new Comparator<int[]>() { public int compare(int[] pair1, int[] pair2) { return pair1[0] != pair2[0] ? pair2[0] - pair1[0] : pair2[1] - pair1[1]; } }); -
填充初始窗口
将前k个元素加入队列:for (int i = 0; i < k; ++i) { pq.offer(new int[]{nums[i], i}); } -
处理第一个窗口的最大值
直接取队首元素的值:ans[0] = pq.peek()[0]; -
滑动窗口并更新结果
从第k个元素开始遍历:- 添加新元素到队列。
- 移除过期元素:循环检查队首元素的索引是否在当前窗口的左侧边界之前(即
<= i - k),若过期则弹出。 - 记录当前窗口的最大值。
for (int i = k; i < n; ++i) { pq.offer(new int[]{nums[i], i}); while (pq.peek()[1] <= i - k) { pq.poll(); } ans[i - k + 1] = pq.peek()[0]; }
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int n = nums.length;
PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>() {
public int compare(int[] pair1, int[] pair2) {
return pair1[0] != pair2[0] ? pair2[0] - pair1[0] : pair2[1] - pair1[1];
}
});
for (int i = 0; i < k; ++i) {
pq.offer(new int[]{nums[i], i});
}
int[] ans = new int[n - k + 1];
ans[0] = pq.peek()[0];
for (int i = k; i < n; ++i) {
pq.offer(new int[]{nums[i], i});
while (pq.peek()[1] <= i - k) {
pq.poll();
}
ans[i - k + 1] = pq.peek()[0];
}
return ans;
}
}