介绍

广义上讲，扩散模型是一种生成式深度学习模型，它通过学习到的去噪过程来创建数据。扩散模型有很多变体，其中最流行的通常是文本条件模型，它可以根据提示生成特定的图像。一些扩散模型（例如 Control-Net）甚至可以将图像与特定的艺术风格融合。以下是一个例子：

如果您不知道图像有什么特别之处，请尝试远离屏幕或眯起眼睛来查看图像中隐藏的秘密。

扩散模型的应用和类型多种多样，但在本教程中，我们将构建基础的非条件扩散模型 DDPM（去噪扩散概率模型）[1]。我们将首先直观地了解该算法的底层工作原理，然后在 PyTorch 中从头构建它。此外，本教程将主要关注该算法背后的直观概念和具体的实现细节。关于数学推导和背景知识，这本书 [2] 是很好的参考资料。

最后说明：此实现是为包含单个 GPU 且兼容 CUDA 的工作流构建的。此外，完整的代码库可在此处找到： 

工作原理 -> 正向和反向过程

图片来自[2] 理解深度学习 作者：Simon JD Prince

扩散过程包括正向过程和逆向过程。正向过程是一个基于噪声表的预定马尔可夫链。噪声表是一组方差B1、B2、…BT，它们控制构成马尔可夫链的条件正态分布。

前向过程马尔可夫链 — 图片来自[2]

这个公式是前向过程的数学表示，但直观上我们可以将其理解为一个序列，我们逐渐将数据示例 X 映射到纯噪声。前向过程中的第一个项只是我们的初始数据示例。在中间时间步长 t，我们有一个带噪声的 X 版本，在最后的时间步长 T，我们得到纯噪声，它大致受标准正态分布的支配。在构建扩散模型时，我们会选择噪声计划。例如，在 DDPM 中，我们的噪声计划具有 1000 个时间步长，方差从 1e-4 线性增加到 0.02。还需要注意的是，我们的前向过程是静态的，这意味着我们选择噪声计划作为扩散模型的超参数，并且我们不会训练前向过程，因为它已经明确定义。还需要注意的是，我们的前向过程是静态的，这意味着我们选择噪声计划作为扩散模型的超参数，并且我们不训练前向过程，因为它已经被明确定义。

关于正向过程，我们必须了解的最后一个关键细节是：由于分布符合正态性，我们可以从数学上推导出一个称为“扩散核”的分布，它表示给定初始数据点，正向过程中任何中间值的分布。这使我们能够绕过在正向过程中迭代添加 t-1 级噪声的所有中间步骤，从而获得包含 t 个噪声的图像，这在以后训练模型时会派上用场。其数学表示为：

扩散核 — 图片来自[2]

其中时间 t 时的 alpha 定义为从初始时间步长到当前时间步长的累积乘积 (1-B)。

逆过程是扩散模型的关键。逆过程本质上是对正向过程的撤销，即逐步从纯噪声图像中去除一定量的噪声，从而生成新的图像。我们从纯噪声数据开始，在每个时间步 t 减去正向过程理论上在该时间步长上添加的噪声量。我们不断去除噪声，直到最终得到与原始数据分布相似的图像。我们的工作重点是训练一个模型，使其能够精确地逼近正向过程，从而估计能够生成新样本的逆向过程。

算法和训练目标

为了训练这样的模型来估计逆扩散过程，我们可以遵循下面定义的图像中的算法：

1. 从我们的训练数据集中随机抽取一个数据点
2. 在我们的噪声（方差）计划中选择一个随机时间步长
3. 将该时间步的噪声添加到我们的数据中，通过“扩散核”模拟正向扩散过程
4. 将我们的去噪图像传入模型，以预测我们添加的噪声
5. 计算预测噪声和实际噪声之间的均方误差，并通过该目标函数优化模型参数
6. 并重复！

DDPM 训练算法——图片来自[2]

从数学上讲，如果没有看到完整的推导，算法中的确切公式一开始可能看起来有点奇怪，但直观地说，它是基于我们的噪声计划的 alpha 值的扩散核的重新参数化，它只是预测噪声和我们添加到图像的实际噪声的平方差。

如果我们的模型能够根据前向过程的特定时间步长成功预测噪声量，我们可以从时间步长 T 的噪声开始迭代，并根据每个时间步长逐渐消除噪声，直到我们恢复类似于原始数据分布中生成的样本的数据。

采样算法总结如下：

1. 从标准正态分布中生成随机噪声

对于从上一个时间步开始并向后移动的每个时间步：

2. 通过估计逆过程分布来更新 Z，其中平均值由上一步的 Z 参数化，方差由我们的模型在该时间步估计的噪声参数化

3. 添加少量噪音以增加稳定性（解释如下）

4. 重复此操作，直到到达时间步 0，即我们恢复的图像！

DDPM采样算法——图片来自[2]

随后采样并生成图像的算法在数学上可能看起来很复杂，但直观上可以归结为一个迭代过程：我们从纯噪声开始，估算在时间步 t 理论上添加的噪声，然后将其减去。如此反复，直到得到生成的样本。唯一需要注意的小细节是，在减去估算的噪声后，我们会再加回少量噪声，以保持过程稳定。例如，在迭代过程开始时一次性估算并减去总噪声会导致样本非常不连贯，因此实践证明，在每个时间步长上加回一点噪声并进行迭代可以生成更好的样本。

UNET

DDPM 论文的作者使用了最初为医学图像分割设计的 UNET 架构，构建了一个用于预测扩散逆过程噪声的模型。本教程中我们将使用的模型适用于 32x32 图像，非常适合 MNIST 等数据集，但该模型可以扩展以处理更高分辨率的数据。UNET 有很多变体，我们将要构建的模型架构概览如下图所示。

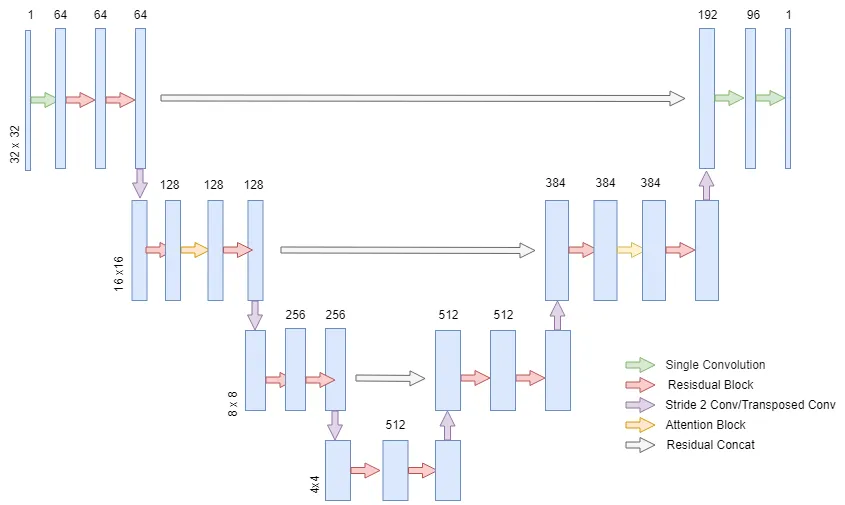
DDPM 的 UNET 与经典 UNET 类似，因为它包含下采样流和上采样流，从而减轻了网络的计算负担，同时在两个流之间具有跳过连接，以合并来自模型浅层和深层特征的信息。

DDPM UNET 与经典 UNET 的主要区别在于，DDPM UNET 在 16x16 维层中引入了注意力机制，并在每个残差块中嵌入了正弦 Transformer 嵌入。正弦嵌入背后的含义是告诉模型我们试图在哪个时间步预测噪声。这通过注入模型在噪声计划中所处位置的信息，帮助模型预测每个时间步的噪声。例如，如果我们有一个噪声计划，其中某些时间步包含大量噪声，那么模型了解它必须预测哪个时间步可以帮助模型预测相应时间步的噪声。对于那些还不熟悉 Transformer 架构的人来说，可以在这里 [3] 找到更多关于注意力机制和嵌入的一般信息。

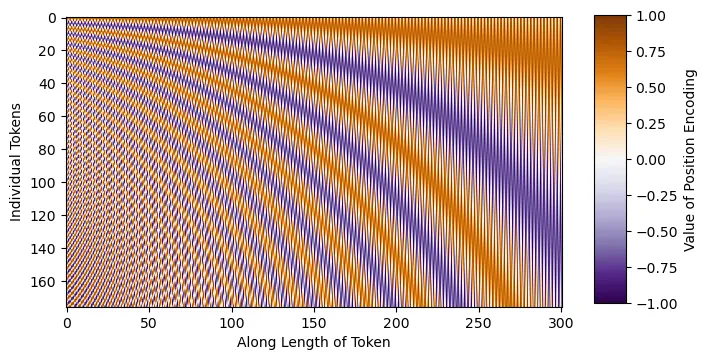
在模型实现中，我们将首先定义导入（pip install 命令已注释，仅供参考），并编写正弦时间步长的嵌入代码。直观地说，正弦嵌入是不同的正弦和余弦频率，可以直接添加到输入中，从而为模型提供额外的位置/顺序理解。如下图所示，每个正弦波都是独一无二的，这将使模型能够感知其在噪声表中的位置。

# 导入
import torch 
import torch.nn as nn 
import torch.nn . functional as F 
from einops import rearrange #pip install einops 
from Typing import  List 
import random 
import math 
from torchvision import datasets, transforms 
from torch.utils.data import DataLoader 
from timm.utils import ModelEmaV3 #pip install timm 
from tqdm import tqdm #pip install tqdm 
import matplotlib.pyplot as plt #pip install matplotlib 
import torch.optim as optim 
import numpy as np 

class  SinusoidalEmbeddings (nn.Module): 
    def  __init__ ( self, time_steps: int , embed_dim: int ): 
        super ().__init__() 
        position = torch.arange(time_steps).unsqueeze( 1 ). float（）
        div = torch.exp（torch.arange（0， embed_dim，2）。float（）* -（math.log（10000.0）/ embed_dim））
        embeddings = torch.zeros（time_steps，embed_dim，requires_grad = False）
        embeddings[:，0 :: 2 ] = torch.sin（position * div）
        embeddings[:，1 :: 2 ] = torch.cos（position * div）
        self.embeddings = embeddings 

    def  forward（self，x，t）：
        embeds = self.embeddings[t].to（x.device）
        返回embeds[:，:，None，None ]

 UNET 每一层的残差块将与原始 DDPM 论文中使用的残差块相同。每个残差块将包含一个组范数序列、ReLU 激活函数、一个 3x3 的“相同”卷积、dropout 和一个跳跃连接。

# 残差块
class  ResBlock (nn.Module): 
    def  __init__ ( self, C: int , num_groups: int , dropout_prob: float ): 
        super ().__init__() 
        self.relu = nn.ReLU(inplace= True ) 
        self.gnorm1 = nn.GroupNorm(num_groups=num_groups, num_channels=C) 
        self.gnorm2 = nn.GroupNorm(num_groups=num_groups, num_channels=C) 
        self.conv1 = nn.Conv2d(C, C, kernel_size= 3 , padding= 1 ) 
        self.conv2 = nn.Conv2d(C, C, kernel_size= 3 , padding= 1 ) 
        self.dropout = nn.Dropout(p=dropout_prob, inplace= True ) 

    def  forward ( self, x, embeddings ): 
        x = x + embeddings[:, :x.shape[ 1 ], :, :] 
        r = self.conv1(self.relu(self.gnorm1(x))) 
        r = self.dropout(r) 
        r = self.conv2(self.relu(self.gnorm2(r)))
        返回r + x

在 DDPM 中，作者在 UNET 的每一层（分辨率尺度）使用了 2 个残差块；对于 16x16 维度的层，我们在两个残差块之间加入了经典的 Transformer 注意力机制。现在，我们将为 UNET 实现注意力机制：

<span style="background-color:#f9f9f9"><span style="color:#242424"> 
     
        

self.proj2 = nn.Linear(C，C)
        self.num_heads = num_heads 
        self.dropout_prob = dropout_prob ( )         x = self.proj1(x)         x = rearrange(x, , K= , H=self.num_heads)         q,k,v = x[ ], x[ , h=h, w=w)         x = self.proj2(x) <span style="color:#c41a16">'bhw C -> b C h w'</span> )

    








        </span></span>

注意力机制的实现非常简单。我们重塑数据，将 h*w 维度组合成一个“序列”维度，类似于 Transformer 模型的经典输入，并将通道维度转换为嵌入特征维度。在此实现中，我们使用 torch.nn. functional.scaled_dot_product_attention，因为此实现包含 Flash 注意力机制，它是注意力机制的优化版本，在数学上仍然等同于经典 Transformer 注意力机制。有关 Flash 注意力机制的更多信息，请参阅以下论文：[4]、[5]。

最后，我们可以定义UNET的完整层：

类 UnetLayer（nn.Module）：
    def  __init__（self，
            upscale：bool，
            attention：bool，
            num_groups：int，
            dropout_prob：float，
            num_heads：int，
            C：int）：
        super（）。__init__（）
        self.ResBlock1 = ResBlock（C = C，num_groups = num_groups，dropout_prob = dropout_prob）
        self.ResBlock2 = ResBlock（C = C，num_groups = num_groups，dropout_prob = dropout_prob）
        如果upscale：
            self.conv = nn.ConvTranspose2d（C，C// 2，kernel_size = 4，stride = 2，padding = 1）
        否则：
            self.conv = nn.Conv2d（C，C * 2，kernel_size = 3，stride = 2， padding= 1）
        如果注意：
            self.attention_layer = Attention（C，num_heads=num_heads，dropout_prob=dropout_prob）

    def  forward（self，x，embeddings）：
        x = self.ResBlock1（x，embeddings）
        如果 hasattr（self，'attention_layer'）：
            x = self.attention_layer（x）
        x = self.ResBlock2（x，embeddings）
        返回self.conv（x），x

如前所述，DDPM 中的每一层都有 2 个残差块，并且可能包含一个注意力机制，我们还会将嵌入传递到每个残差块中。此外，我们还会返回下采样或上采样值以及先验值，我们将存储该值并将其用于残差级联跳跃连接。

最后，我们可以完成 UNET 课程：

类 UNET（nn.Module）：
    def  __init__（self，
            Channels：List = [ 64 , 128 , 256 , 512 , 512 , 384 ]，
            Attentions：List = [ False , True , False , False , False , True ]，
            Upscales：List = [ False , False , False , True , True , True ]，
            num_groups：int = 32，
            dropout_prob：float = 0.1，
            num_heads：int = 8，
            input_channels：int = 1，
            output_channels：int = 1，
            time_steps：int = 1000）：
        super（）。__init__（）
        self.num_layers = len（Channels）
        self.shallow_conv = nn.Conv2d（input_channels，通道[ 0 ]，内核大小= 3，填充= 1）
        out_channels =（通道[- 1 ]// 2）+通道[ 0 ] 
        self.late_conv = nn.Conv2d（out_channels，out_channels// 2，内核大小= 3，填充= 1）
        self.output_conv = nn.Conv2d（out_channels// 2，output_channels，内核大小= 1）
        self.relu = nn.ReLU（inplace = True）
        self.embeddings = SinusoidalEmbeddings（time_steps = time_steps，embed_dim = max（通道））
        对于范围内的 i （self.num_layers）：            layer = UnetLayer（                upscale = Upscales [i]，                attention = Attentions [i]，                num_groups = num_groups，                dropout_prob=dropout_prob，                C=Channels[i]，                num_heads=num_heads             ）setattr








            （self，f'Layer {i + 1 } '，layer）

    def  forward（self，x，t）：
        x = self.shallow_conv（x）
        residuals = [] 
        for i in  range（self.num_layers // 2）：
            layer = getattr（self，f'Layer {i + 1 } '）
            embeddings = self.embeddings（x，t）
            x，r = layer（x，embeddings）
            residuals.append（r）
        for i in  range（self.num_layers // 2，self.num_layers）：
            layer = getattr（self，f'Layer {i + 1 } '）
            x = torch.concat（（layer（x，embeddings）[ 0 ]，residuals[self.num_layers-i- 1 ]），dim= 1）
        return self.output_conv（self.relu（self.late_conv（x）））

基于我们已经创建的类，实现起来非常简单。此实现的唯一区别在于，我们的上游通道比 UNET 的典型通道略大。我发现，这种架构在配备 16GB VRAM 的单 GPU 上训练效率更高。

调度程序

为 DDPM 编写噪声/方差调度程序也非常简单。在 DDPM 中，我们的调度将从 1e-4 开始，如前所述，以 0.02 结束，并呈线性增长。

类 DDPM_Scheduler（nn.Module）：
    def  __init__（self，num_time_steps：int = 1000）：
        super（）。__init__（）
        self.beta = torch.linspace（1e- 4，0.02 ，num_time_steps，requires_grad = False ） alpha 
        = 1 -self.beta 
        self.alpha = torch.cumprod（alpha，dim = 0）.requires_grad_（False）

    def  forward（self，t）：
        返回self.beta [t]，self.alpha [t]

我们返回 beta（方差）值和 alpha 值，因为我们的训练和采样公式使用这两个值都是基于它们的数学推导。

def  set_seed（种子：int = 42）：
    torch.manual_seed（种子）
    torch.cuda.manual_seed_all（种子）
    torch.backends.cudnn.deterministic = True
     torch.backends.cudnn.benchmark = False
     np.random.seed（种子）
    random.seed（种子）

此外（非必需），此函数定义了一个训练种子。这意味着，如果您想重现特定的训练实例，可以使用一组种子，这样每次使用相同的种子时，随机权重和优化器初始化都是相同的。

训练

为了实现这一目标，我们将创建一个模型来生成 MNIST 数据（手写数字）。由于 PyTorch 默认这些图像的尺寸为 28x28，因此我们将图像填充到 32x32，以遵循原始论文中在 32x32 图像上训练的方法。

为了进行优化，我们使用 Adam，初始学习率为 2e-5。我们还使用 EMA（指数移动平均线）来辅助提高生成质量。EMA 是模型参数的加权平均值，在推理时间内可以创建更平滑、噪声更低的样本。对于此实现，我使用了 timm 库的 EMAV3 开箱即用实现，权重为 0.9999，与 DDPM 论文中使用的相同。

总结一下我们的训练过程，我们只需遵循上面的伪代码即可。我们为批次随机选取时间步长，并根据这些时间步长的计划对批次中的数据进行噪声处理，然后将该批次的噪声图像与时间步长本身一起输入到 UNET 中，以指导正弦嵌入。我们使用伪代码中基于“扩散核”的公式对图像进行噪声处理。然后，我们将模型对噪声添加量的预测与实际添加的噪声进行比较，并优化噪声的均方误差。我们还实现了基本的检查点，以便在不同的时期暂停和恢复训练。

def  train（batch_size：int = 64，
          num_time_steps：int = 1000，
          num_epochs：int = 15，
          seed：int = - 1，
          ema_decay：float = 0.9999，   
          lr = 2e-5，
          checkpoint_path：str = None）：
    set_seed（random.randint（0，2 ** 32 - 1））如果seed == - 1 ，则设置seed（seed）    train_dataset = datasets.MNIST（root = '。/ data '，train = True，download = False，transform = transforms.ToTensor（））    train_loader = DataLoader（train_dataset，batch_size = batch_size，shuffle = True，drop_last = True，num_workers = 4）    scheduler = DDPM_Scheduler（num_time_steps=num_time_steps）    model = UNET（）。cuda（）    优化器 = optim.Adam（model.parameters（，lr=lr）    ema = ModelEmaV3（model，decay=ema_decay）如果checkpoint_path不为None：        checkpoint = torch.load（checkpoint_path）        model.load_state_dict（checkpoint [ 'weights' ]）        ema.load_state_dict（checkpoint [ 'ema' ]）        optimizer.load_state_dict（checkpoint [ 'optimizer' ]）    criterion = nn.MSELoss（reduction= 'mean'）对于范围内的i （num_epochs）：        total_loss = 0 for bidx，（x，_）在枚举中（tqdm（train_loader，desc= f“Epoch {i + 1 } / {num_epochs} “））：            x = x.cuda()             x = F.pad(x, ( 2 , 2 , 2 , 2 ))             t = torch.randint( 0 ,num_time_steps,(batch_size,))             e = torch.randn_like(x, require_grad= False )             a = Scheduler.alpha[t].view(batch_size, 1 , 1 , 1 








      






     

         




).cuda() 
            x = (torch.sqrt(a)*x) + (torch.sqrt( 1 -a)*e)
            输出 = 模型(x，t)
            优化器.zero_grad()
            损失 = 标准(输出，e) 
            total_loss += loss.item() 损失
            .backward()
            优化器.step() 
            ema.update(模型)
        打印( f'Epoch {i + 1 } | 损失{total_loss / ( 60000 /batch_size): .5 f} ' )

    检查点 = { 
        '权重'：模型.state_dict()，
        '优化器'：优化器.state_dict()，
        'ema'：ema.state_dict() 
    } 
    torch.save(检查点，'检查点/ddpm_checkpoint' )

对于推理，我们完全遵循伪代码的另一部分。直观地说，我们只是将正向过程反转。我们从纯噪声开始，现在训练好的模型可以预测每个时间步的估计噪声，然后可以迭代地生成全新的样本。对于每个不同的噪声起点，我们可以生成一个不同的独特样本，该样本与原始数据分布相似，但又独一无二。本文并未推导推理公式，但开头链接的参考文献可以为想要深入了解的读者提供指导。

还要注意，我包含了一个辅助函数来查看漫射图像，以便您可以直观地看到模型学习逆向过程的程度。

def  display_reverse（images：List）：fig，axes = plt.subplots（1，10 ， figsize 
    = （ 10，1 ））对于i，ax in enumerate （ axes.flat）：        x = images[i].squeeze（0 ） x         = rearrange（x，'chw -> hw c'）        x = x.numpy（）        ax.imshow（x）        ax.axis（'off'）    plt.show（）def inference（checkpoint_path：str = None，              num_time_steps：int = 1000，              ema_decay：float = 0.9999，）：    checkpoint = torch.load（checkpoint_path）    model = UNET（）。cuda（）    model.load_state_dict（checkpoint [ 'weights'）    ema = ModelEmaV3（model，decay = ema_decay）    ema.load_state_dict（checkpoint [ ' ema ' ]）调度程序    = DDPM_Scheduler（num_time_steps = num_time_steps ）时间=     [ 0，15，50，100，200，300，400，550，700，999 ]图像    = [ ]与torch.no_grad （）：模型= ema.module         。eval ()对于范围（10 ）内的i ：            z = torch.randn( 1 , 1 , 32 , 32 )对于反转的t （范围（1，num_time_steps））：                t = [t]                 temp = (scheduler.beta[t]/( (torch.sqrt( 1 -scheduler.alpha[t]))*(torch.sqrt( 1 -scheduler.beta[t])) ))                 z = ( 1 /(torch.sqrt( 1 -scheduler.beta[t])))*z - (temp*model(z.cuda(),t).cpu())如果t[ 0 ]在时间中：                    images.append(z)                 e = torch.randn( 1 , 1 , 32 ,
     







 











    

         

             



                

32 ) 
                z = z + (e*torch.sqrt(scheduler.beta[t])) 
            temp = Scheduler.beta[ 0 ]/( (torch.sqrt( 1 -scheduler.alpha[ 0 ]))*(torch.sqrt( 1 -scheduler.beta[ 0 ])) ) 
            x = ( 1 /(torch.sqrt( 1 -scheduler.beta[ 0 ])))*z - (temp*model(z.cuda(),[ 0 ]).cpu()) 

            images.append(x) 
            x = rearrange(x.squeeze( 0 ), 'chw -> hw c' ).detach() 
            x = x.numpy() 
            plt.imshow(x) 
            plt.show() 
            display_reverse(images) 
            images = []

def  main（）：
    训练（checkpoint_path = 'checkpoints / ddpm_checkpoint'，lr = 2e-5，num_epochs = 75）
    推理（'checkpoints / ddpm_checkpoint'）

如果__name__ == '__main__'：
    main（）

按照上面列出的实验细节进行 75 个 epoch 训练后，我们得到了以下结果：

此时，我们刚刚在 PyTorch 中从头开始编写了 DDPM 代码！