基于FPGA的一维时间序列idct变换verilog实现,包含testbench和matlab辅助验证程序

news2025/4/22 13:02:16

目录

1.算法运行效果图预览

2.算法运行软件版本

3.部分核心程序

4.算法理论概述

4.1 DCT离散余弦变换

4.2 IDCT逆离散余弦变换

4.3 树结构实现1024点IDCT的原理

5.算法完整程序工程

1.算法运行效果图预览

(完整程序运行后无水印)

matlab仿真结果

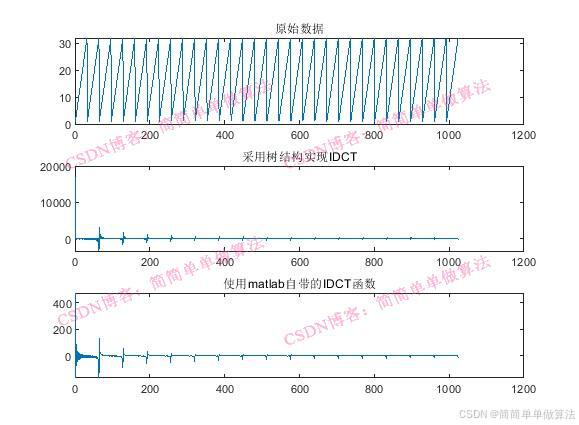
FPGA仿真结果

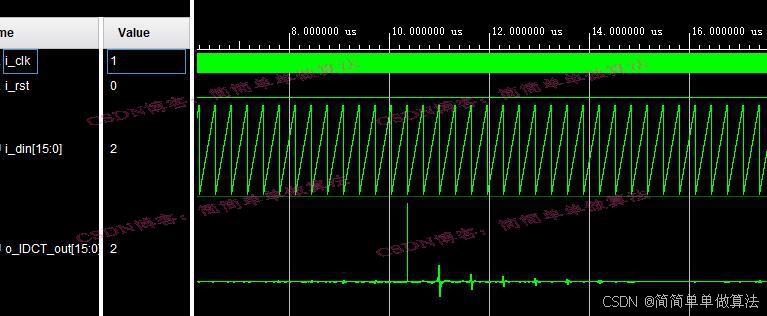
       由于FPGA中的数据通常采用定点表示，在计算过程中会引入量化和舍入误差。因此，上述FPGA的测试结果，在数值较小时，和MATLAB存在一点误差。

2.算法运行软件版本

vivado2019.2

Matlab2022a

3.部分核心程序

（完整版代码包含详细中文注释和操作步骤视频）

`timescale 1ns / 1ps
//
// Company: 
// Engineer: 
// 
// Create Date:    19:52:27 04/01/2014 
// Design Name: 
// Module Name:    myDD16 
// Project Name: 
// Target Devices: 
// Tool versions: 
// Description: 
//
// Dependencies: 
//
// Revision: 
// Revision 0.01 - File Created
// Additional Comments: 
//
//
module myDD16(
              x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,
              Z1,Z2,Z3,Z4,Z5,Z6,Z7,Z8,Z9,Z10,Z11,Z12,Z13,Z14,Z15,Z16
	          );
				 
input signed[15:0] x1;
input signed[15:0] x2;
input signed[15:0] x3;
input signed[15:0] x4;
input signed[15:0] x5;
input signed[15:0] x6;
input signed[15:0] x7;
input signed[15:0] x8;
input signed[15:0] x9;
input signed[15:0] x10;
input signed[15:0] x11;
input signed[15:0] x12;
input signed[15:0] x13;
input signed[15:0] x14;
input signed[15:0] x15;
input signed[15:0] x16;
output signed[15:0]Z1;
output signed[15:0]Z2;
output signed[15:0]Z3;
output signed[15:0]Z4;
output signed[15:0]Z5;
output signed[15:0]Z6;
output signed[15:0]Z7;
output signed[15:0]Z8;
output signed[15:0]Z9;
output signed[15:0]Z10;
output signed[15:0]Z11;
output signed[15:0]Z12;
output signed[15:0]Z13;
output signed[15:0]Z14;
output signed[15:0]Z15;
output signed[15:0]Z16;


//STEP1
//STEP1
wire signed[15:0]s11_1;
wire signed[15:0]s11_2;
wire signed[15:0]s11_3;
wire signed[15:0]s11_4;
wire signed[15:0]s11_5;
wire signed[15:0]s11_6;
wire signed[15:0]s11_7;
wire signed[15:0]s11_8;

assign s11_1 = x1 + x16;
assign s11_2 = x2 + x15;
assign s11_3 = x3 + x14;
assign s11_4 = x4 + x13;
assign s11_5 = x5 + x12;
assign s11_6 = x6 + x11;
assign s11_7 = x7 + x10;
assign s11_8 = x8 + x9;

wire signed[31:0]s12t_1;
wire signed[31:0]s12t_2;
wire signed[31:0]s12t_3;
wire signed[31:0]s12t_4;
wire signed[31:0]s12t_5;
wire signed[31:0]s12t_6;
wire signed[31:0]s12t_7;
wire signed[31:0]s12t_8;
assign s12t_1 = (x1 - x16)*32610;
assign s12t_2 = (x2 - x15)*31357;
assign s12t_3 = (x3 - x14)*28899;
assign s12t_4 = (x4 - x13)*25330;
assign s12t_5 = (x5 - x12)*20788;
assign s12t_6 = (x6 - x11)*15447;
assign s12t_7 = (x7 - x10)*9512;
assign s12t_8 = (x8 - x9)*3212;
 

wire signed[15:0]s12_1;
wire signed[15:0]s12_2;
wire signed[15:0]s12_3;
wire signed[15:0]s12_4;
wire signed[15:0]s12_5;
wire signed[15:0]s12_6;
wire signed[15:0]s12_7;
wire signed[15:0]s12_8;
assign s12_1 = s12t_1[29:14];
assign s12_2 = s12t_2[29:14];
assign s12_3 = s12t_3[29:14];
assign s12_4 = s12t_4[29:14];
assign s12_5 = s12t_5[29:14];
assign s12_6 = s12t_6[29:14];
assign s12_7 = s12t_7[29:14];
assign s12_8 = s12t_8[29:14];


//STEP2
//STEP2
wire signed[15:0]Y1_1;
wire signed[15:0]Y1_2;
wire signed[15:0]Y1_3;
wire signed[15:0]Y1_4;
wire signed[15:0]Y1_5;
wire signed[15:0]Y1_6;
wire signed[15:0]Y1_7;
wire signed[15:0]Y1_8;
wire signed[15:0]Y2_1;
wire signed[15:0]Y2_2;
wire signed[15:0]Y2_3;
wire signed[15:0]Y2_4;
wire signed[15:0]Y2_5;
wire signed[15:0]Y2_6;
wire signed[15:0]Y2_7;
wire signed[15:0]Y2_8;
myDD8 U1(
.x1(s11_1),
.x2(s11_2),
.x3(s11_3),
.x4(s11_4),
.x5(s11_5),
.x6(s11_6),
.x7(s11_7),
.x8(s11_8),
.Z1(Y1_1),
.Z2(Y1_2),
.Z3(Y1_3),
.Z4(Y1_4),
.Z5(Y1_5),
.Z6(Y1_6),
.Z7(Y1_7),
.Z8(Y1_8)
);
myDD8 U2(
.x1(s12_1),
.x2(s12_2),
.x3(s12_3),
.x4(s12_4),
.x5(s12_5),
.x6(s12_6),
.x7(s12_7),
.x8(s12_8),
.Z1(Y2_1),
.Z2(Y2_2),
.Z3(Y2_3),
.Z4(Y2_4),
.Z5(Y2_5),
.Z6(Y2_6),
.Z7(Y2_7),
.Z8(Y2_8)
);


//Reorder
//Reorder

assign Z1=Y1_1;
assign Z3=Y1_2;
assign Z5=Y1_3;
assign Z7=Y1_4;
assign Z9=Y1_5;
assign Z11=Y1_6;
assign Z13=Y1_7;
assign Z15=Y1_8;
assign Z2={Y2_1[15],Y2_1[15:1]};
assign Z4=Y2_2-Z2;
assign Z6=Y2_3-Z4;
assign Z8=Y2_4-Z6;
assign Z10=Y2_5-Z8;
assign Z12=Y2_6-Z10;
assign Z14=Y2_7-Z12;
assign Z16=Y2_8-Z14;
 

endmodule
23_019m

4.算法理论概述

      在数字信号处理领域，离散余弦变换（Discrete Cosine Transform, DCT）及其逆变换（Inverse Discrete Cosine Transform, IDCT）扮演着重要角色。

4.1 DCT离散余弦变换

       对于一个长度为 N 的一维离散信号 x(n)，n=0,1,⋯,N−1，其 N 点离散余弦变换（DCT - II）定义为：

4.2 IDCT逆离散余弦变换

4.3 树结构实现1024点IDCT的原理

       树结构实现 1024 点 IDCT 的核心思想是分治策略。将一个 1024 点的 IDCT 问题分解为两个 512 点的 IDCT 问题，每个 512 点的 IDCT 问题又可以进一步分解为两个 256 点的 IDCT 问题，以此类推，直到分解为 8 点的 IDCT 问题。

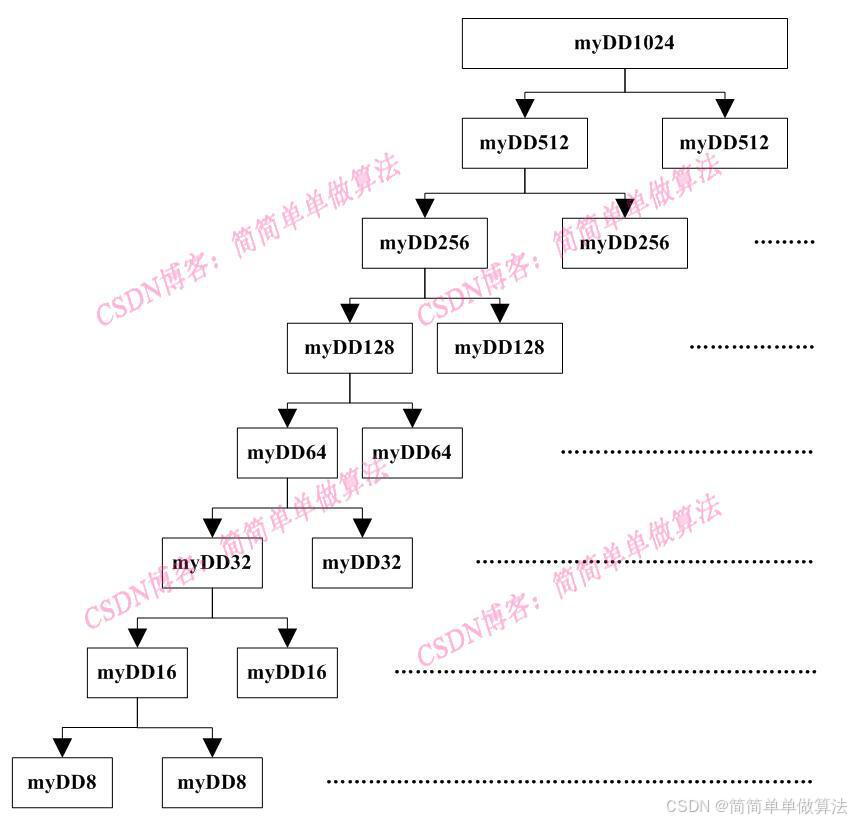
      通过上述的结构，最终可以将问题归结为8点IDCT的计算。对于8点IDCT，设输入系数为Z(k)，k=0,1,⋯,7，输出为z(n)，n=0,1,⋯,7，其计算公式为：

       具体来说，首先对输入的1024点IDCT系数进行分组，得到两个512点IDCT的输入系数；然后对每个512点IDCT的输入系数再进行分组，得到两个256点IDCT的输入系数，以此类推，直到得到多个8点IDCT的输入系数。接着，计算所有8点IDCT的结果；再根据这些结果计算256点IDCT的结果；然后根据256点IDCT的结果计算512点IDCT的结果；最后根据512点IDCT的结果计算1024点IDCT的结果。

5.算法完整程序工程

OOOOO

OOO

O

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2340114.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Linux进程5-进程通信常见的几种方式、信号概述及分类、kill函数及命令、语法介绍

Linux进程5-进程通信常见的几种方式、信号概述及分类、kill函数及命令、语法介绍

目录 1.进程间通信概述 1.1进程通信的主要方式 1.2进程通信的核心对比 2.信号 2.1 信号的概述 2.1.1 信号的概念 2.2信号的核心特性 2.3信号的产生来源 2.4信号的处理流程 2.5关键系统调用与函数 2.6常见信号的分类及说明 2.6.1. 标准信号（Standard Sig…
阅读更多...
[架构之美]一键服务管理大师：Ubuntu智能服务停止与清理脚本深度解析

[架构之美]一键服务管理大师：Ubuntu智能服务停止与清理脚本深度解析

[架构之美]一键服务管理大师：Ubuntu智能服务停止与清理脚本深度解析 服务展示： 运行脚本： 剩余服务： 一、脚本设计背景与核心价值 在Linux服务器运维中，服务管理是日常操作的重要环节。本文介绍的智能服务管理脚本&a…
阅读更多...
C++算法（10）：二叉树的高度与深度，（C++代码实战）

C++算法（10）：二叉树的高度与深度，（C++代码实战）

引言 在二叉树的相关算法中，高度（Height）和深度（Depth）是两个容易混淆的概念。本文通过示例和代码实现，帮助读者清晰区分二者的区别。 定义与区别 属性定义计算方式深度从根节点到该节点的边数根节点深度…
阅读更多...
Psychology 101 期末测验（附答案）

Psychology 101 期末测验（附答案）

欢呼 啦啦啦~啦啦啦~♪(^∇^*) 终于考过啦~ 开心(*^▽^*) 撒花✿✿ヽ(▽)ノ✿ |必须晒下证书： 判卷 记录下判卷，还是错了几道，填空题2道压根填不上。惭愧~ 答案我隐藏了，实在想不出答案的朋友可以留言，不定时回复。 建议还是认认真真的学习~认认真真的考试~，知识就…
阅读更多...
安全协议分析概述

安全协议分析概述

一、概念 安全协议（security protocol），又称密码协议。是以密码学为基础的消息交换协议，在网络中提供各种安全服务。（为解决网络中的现实问题、满足安全需求） 1.1 一些名词 那什么是协议呢？ …
阅读更多...
基础学习：（7）nanoGPT 剩下的细节

基础学习：（7）nanoGPT 剩下的细节

文章目录 前言3 继续巴拉结构3.1 encode 和 embedding3.2 全局layernorm3.3 lm_head(language modeling) 和 softmax3.4 softmax 和 linear 之间的 temperature和topk3.5 weight tying 前言 在 基础学习：（6）中, 在运行和训练代码基础上,向代…
阅读更多...
Spark-SQL连接Hive总结及实验

Spark-SQL连接Hive总结及实验

一、核心模式与配置要点 1. 内嵌Hive 无需额外配置，直接使用，但生产环境中几乎不使用。 2. 外部Hive（spark-shell连接） 配置文件：将hive-site.xml（修改数据库连接为node01）、core-site.xml、…
阅读更多...
Linux Wlan-四次握手(eapol)框架流程

Linux Wlan-四次握手(eapol)框架流程

协议基础 基于 IEEE 802.1X 标准实现的协议 抓包基础 使用上一章文章的TPLINK wn722n v1网卡在2.4G 频段抓包（v2、v3是不支持混杂模式的） eapol的四个交互流程 根据不同的认证模式不同，两者的Auth流程有所不同，但是握手流程基…
阅读更多...
web组件和http协议

web组件和http协议

1.web组件 2.自定义元素 3.影子DOM 4.HTML模板 5.http协议 6.tcp ip协议
阅读更多...
软件工程师中级考试-上午知识点总结（下）

软件工程师中级考试-上午知识点总结（下）

6. 知识产权和标准化 软件著作权客体：指的是受软件著作权保护的对象，即计算机程序和相关文档。知识产权具有严格的地域性。不受保护期限制：著名权、修改权、保护作品完整权；注意的是，发表权受保护期限制。专利权在期满…
阅读更多...
IO流--字节流详解

IO流--字节流详解

IO流 用于读写数据的（可以读写文件，或网络中的数据） 概述： I指 Input，称为输入流：负责从磁盘或网络上将数据读到内存中去 O指Output，称为输出流，负责写数据出去到网络或磁盘上 因…
阅读更多...
Cesium学习笔记——dem/tif地形的分块与加载

Cesium学习笔记——dem/tif地形的分块与加载

前言 在Cesium的学习中，学会读文档十分重要！！！在这里附上Cesium中英文文档1.117。 在Cesium项目中，在平坦坦地球中加入三维地形不仅可以增强真实感与可视化效果，还可以​​提升用户体验与交互性&#xff0c…
阅读更多...
Java排序算法百科全书：原理、实现与实战指南

Java排序算法百科全书：原理、实现与实战指南

一、排序算法全景视图 1. 算法分类体系 graph TDA[排序算法] --> B[比较排序]A --> C[非比较排序]B --> B1[基本排序]B1 --> B11[冒泡排序]B1 --> B12[选择排序]B1 --> B13[插入排序]B --> B2[高效排序]B2 --> B21[快速排序]B2 --> B22[归并排序]B…
阅读更多...
开源脚本分享：用matlab处理ltspice生成的.raw双脉冲数据

开源脚本分享：用matlab处理ltspice生成的.raw双脉冲数据

Author :PNJIE DATE: 2025/04/21 V0.0 前言 该项目旨在使用Matlab处理LTspice的.raw文件，包括动态计算和绘图，部分脚本基于LTspice2Matlab项目： PeterFeicht/ltspice2matlab: LTspice2Matlab - 将LTspice数据导入MATLAB github地址&#x…
阅读更多...
(二)mac中Grafana监控Linux上的MySQL(Mysqld_exporter)

(二)mac中Grafana监控Linux上的MySQL(Mysqld_exporter)

框架：GrafanaPrometheusMysqld_exporter 一、监控查看端安装 Grafana安装-CSDN博客 普罗米修斯Prometheus监控安装（mac）-CSDN博客 1.启动Grafana服务 brew services start grafana 打开浏览器输入http://localhost:3000进入grafana登录…
阅读更多...
Github中项目的公开漏洞合集

Github中项目的公开漏洞合集

前言 最近在搜CVE的时候，意外发现了GitHub Security Advisories。 可能对一些人来说，已经是老东西了。但我还是第一次见到。 觉得挺好用的，就分享出来。 GitHub Security Advisories GitHub Security Advisories 是 GitHub 提供的一项重要…
阅读更多...
蚂蚁全媒体总编刘鑫炜再添新职，出任共工新闻社新媒体研究院院长

蚂蚁全媒体总编刘鑫炜再添新职，出任共工新闻社新媒体研究院院长

2025年4月18日，共工新闻社正式宣布聘任蚂蚁全媒体总编刘鑫炜为新媒体研究院院长。此次任命标志着刘鑫炜在新媒体领域的专业能力与行业贡献再次获得权威机构认可。 刘鑫炜深耕新媒体领域多年，曾担任中国新闻传媒集团新媒体研究院院长、蚂蚁全媒体总编等职…
阅读更多...
吴恩达强化学习复盘(2)K-Means初始化|K的选择|算法优化

吴恩达强化学习复盘(2)K-Means初始化|K的选择|算法优化

K-Means初始化 K-Means 算法的第一步是随机选择位置作为初始聚类中心（new one through newk），但如何进行随机猜测是需要探讨的问题。一般需要多次尝试初始猜测，以期望找到更好的聚类结果。 K 值选择及初始聚类中心选取方法 K 值…
阅读更多...
SQL优化案例分享 | PawSQL 近日推出 Lateral Join 重写优化算法

SQL优化案例分享 | PawSQL 近日推出 Lateral Join 重写优化算法

一、Lateral 查询语法介绍 Lateral 查询是SQL中的一种连接方式，它允许FROM子句中的子查询引用同一FROM子句中前面的表的列。虽然这种特性提供了强大的表达能力，但在某些场景下可能导致性能问题。PawSQL优化器近日实现了一种针对特定类型Lateral Join的重…
阅读更多...
电子电器架构 ---软件定义汽车的电子/电气（E/E）架构

电子电器架构 ---软件定义汽车的电子/电气（E/E）架构

我是穿拖鞋的汉子，魔都中坚持长期主义的汽车电子工程师。 老规矩，分享一段喜欢的文字，避免自己成为高知识低文化的工程师： 周末洗了一个澡，换了一身衣服，出了门却不知道去哪儿，不知道去找谁，漫无目的走着，大概这就是成年人最深的孤独吧! 旧人不知我近况，新人不知我过…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023