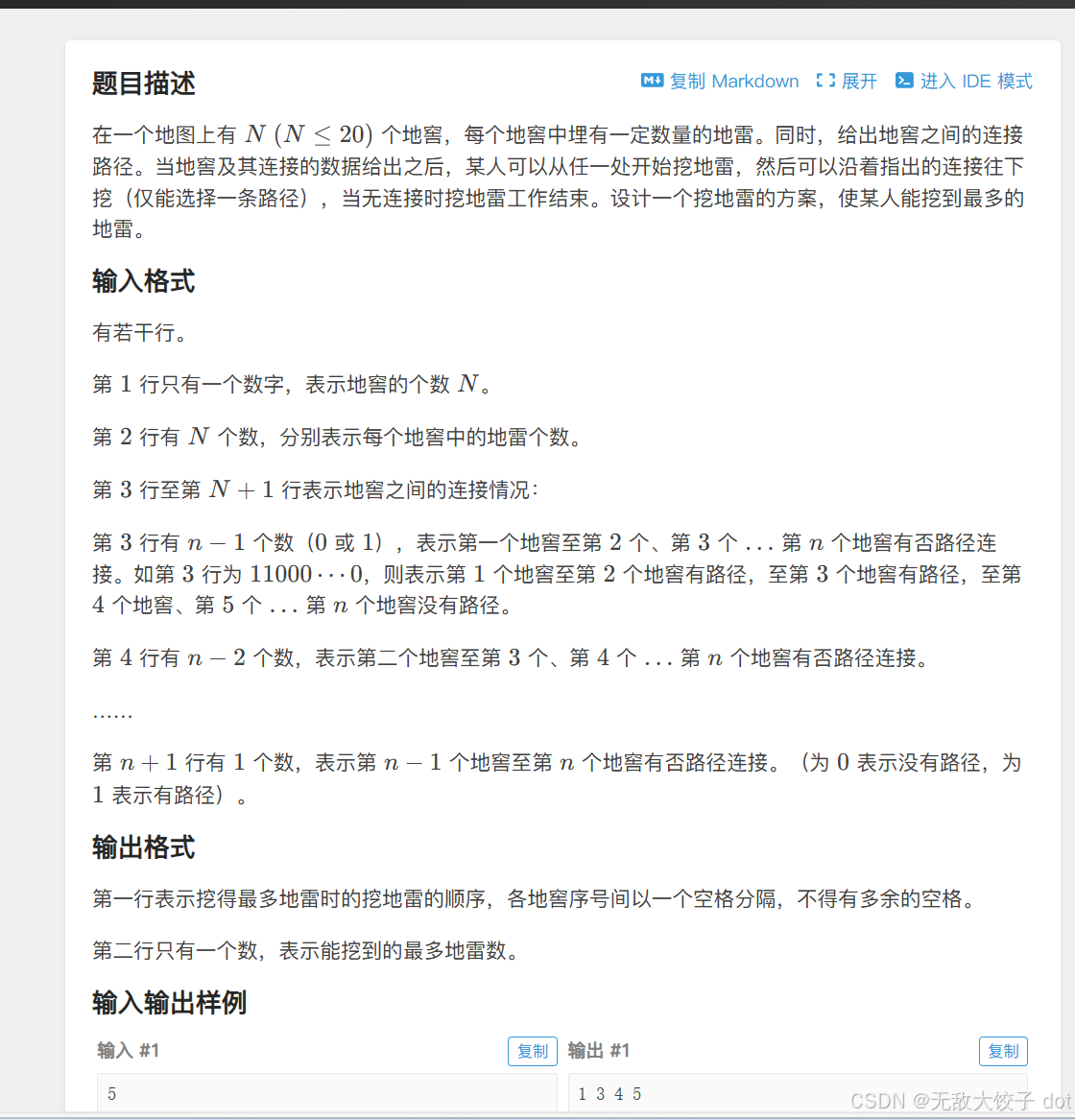
这道题其实就是正常的最长上升子序列问题，但是我们还要把最优方案输出出来，我们可以用个pre数组来维护就行了，每当我们更新以i为结尾的最长子序列，如果i是接在1到i-1某个点后面的话就把前面的点存到pre里面

最后我们把pre倒着打印一遍就是我们的原方案了

好的，我们还是按照动态规划dp的套路来做一哈

step1>定义状态表示 f[i]表示以i为结尾的时候最长子序列长度

step2>推导状态转移方程

废话不多说，实现一下我们的代码！

例：这种其实就是一个有向图的邻接矩阵

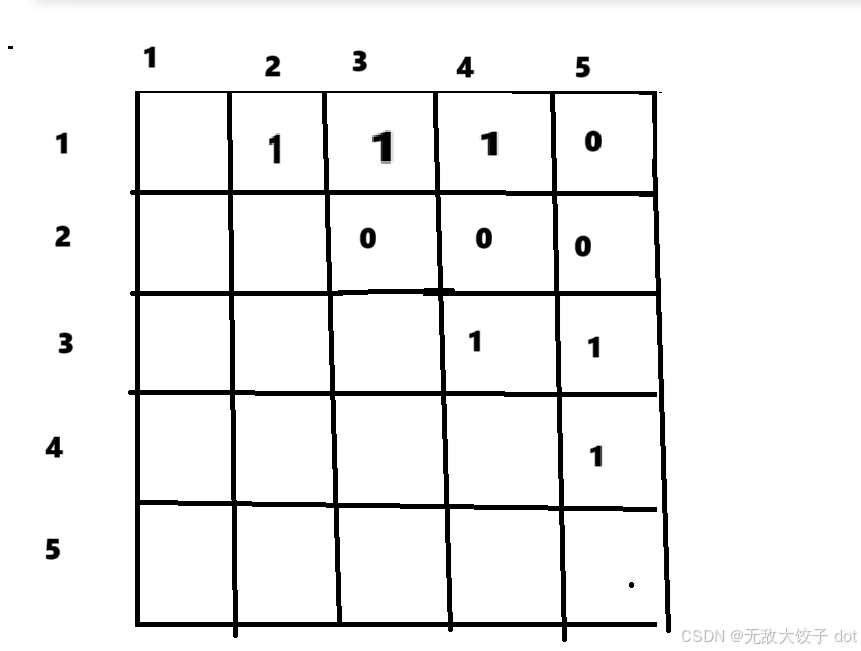
我们用动态规划最长上升子序列的方式，枚举每个地窖结尾的最长子序列，找到最长的那个子序列，输出它

#include <iostream>

using namespace std;
const int N = 35;
int n;
int cnt[N];
int f[N];
int pre[N];
int edges[N][N];
void dfs(int x)
{
	if(pre[x]) dfs(pre[x]);
	cout << x << " ";
}
int main()
{
	cin >> n;
	for(int i = 1;i<=n;i++)
	{
		cin >> cnt[i];
	}
	for(int i = 1;i<n;i++)
	{
		for(int j = i+1;j<=n;j++)
		{
			cin >> edges[i][j];
		}
	}
	int ret = 0;
	for(int i =1;i<=n;i++)
	{
		f[i] = cnt[i];
		for(int j = 1;j<i;j++)
		{
			if(edges[j][i]) 
			{
				if(f[j]+cnt[i] > f[i])
				{
					pre[i] = j;
					f[i] = f[j]+cnt[i];
				}
			}
		}
		ret = max(ret,f[i]);
	}
	int j = 0;
	for(int i = 1;i<=f[i];i++)
	{
		if(f[i] > f[j]) j=i; 
	}
	dfs(j);
	cout << endl;
	cout << ret << endl;
	
	
	return 0;
}