题目描述
给定一个包含 n + 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ,返回 这个重复的数 。
你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。
示例 1:
输入:nums = [1,3,4,2,2] 输出:2
示例 2:
输入:nums = [3,1,3,4,2] 输出:3
提示:
1 <= n <= 105nums.length == n + 11 <= nums[i] <= nnums中 只有一个整数 出现 两次或多次 ,其余整数均只出现 一次
进阶:
- 如何证明
nums中至少存在一个重复的数字? - 你可以设计一个线性级时间复杂度
O(n)的解决方案吗?
方法一:二分查找
实现思路:
依据什么属性查找?我们知道,一个数组在某个属性上有单调性,就可以进行二分查找(比如排序数组的数组值)。那升序的数组对于本题来说还有什么单调性呢。这个单调性就是: 数组的索引越大,数组值就越大,数组值越大,原数组中小于等于这个数组值的数就越多。 举个例子你就懂了:
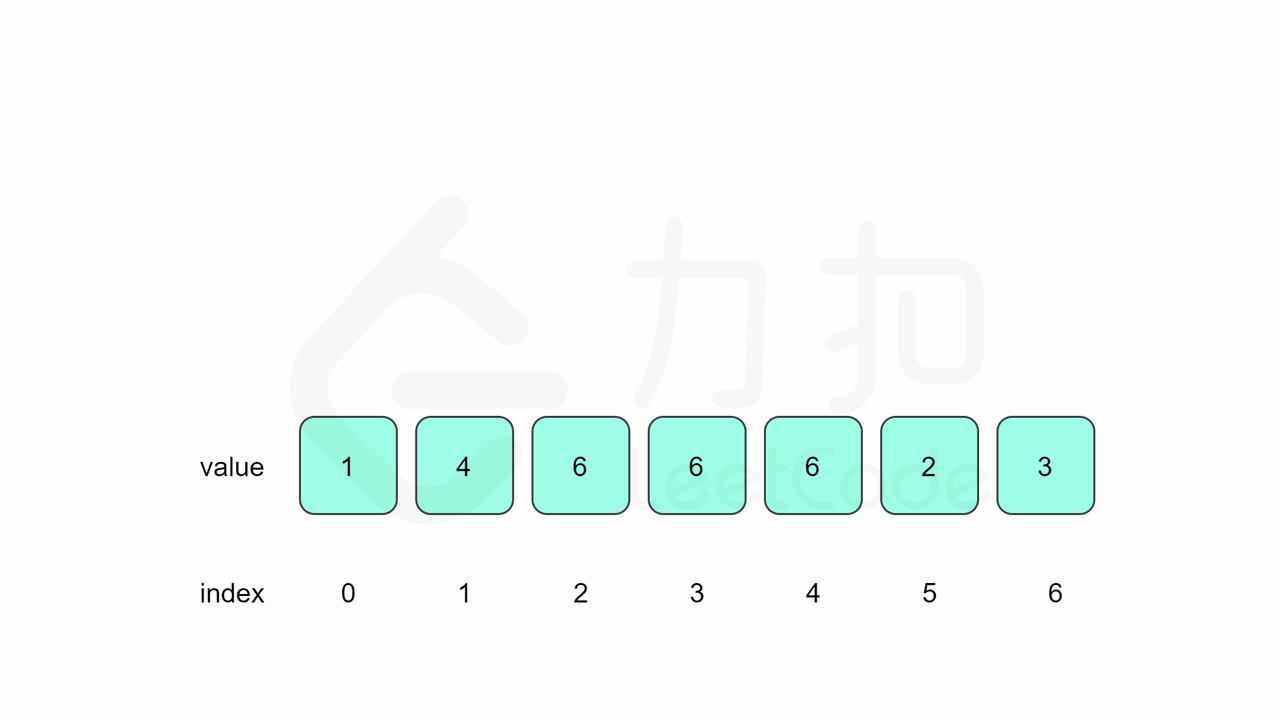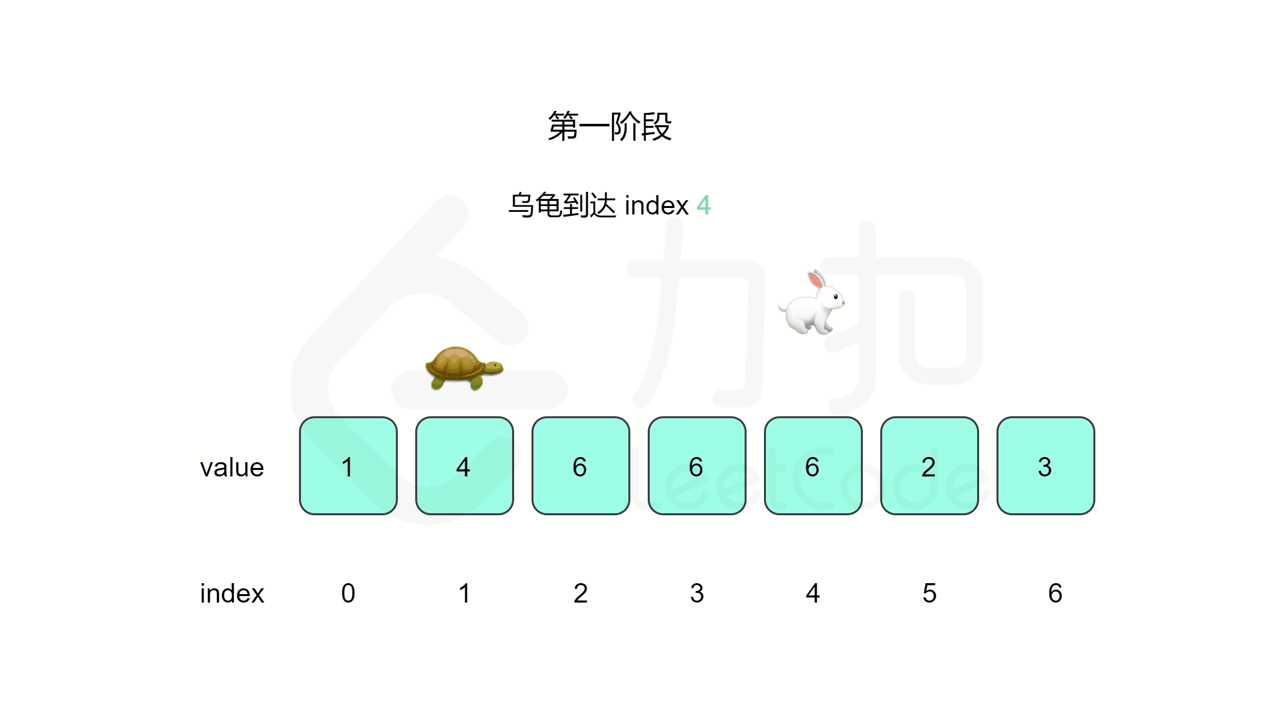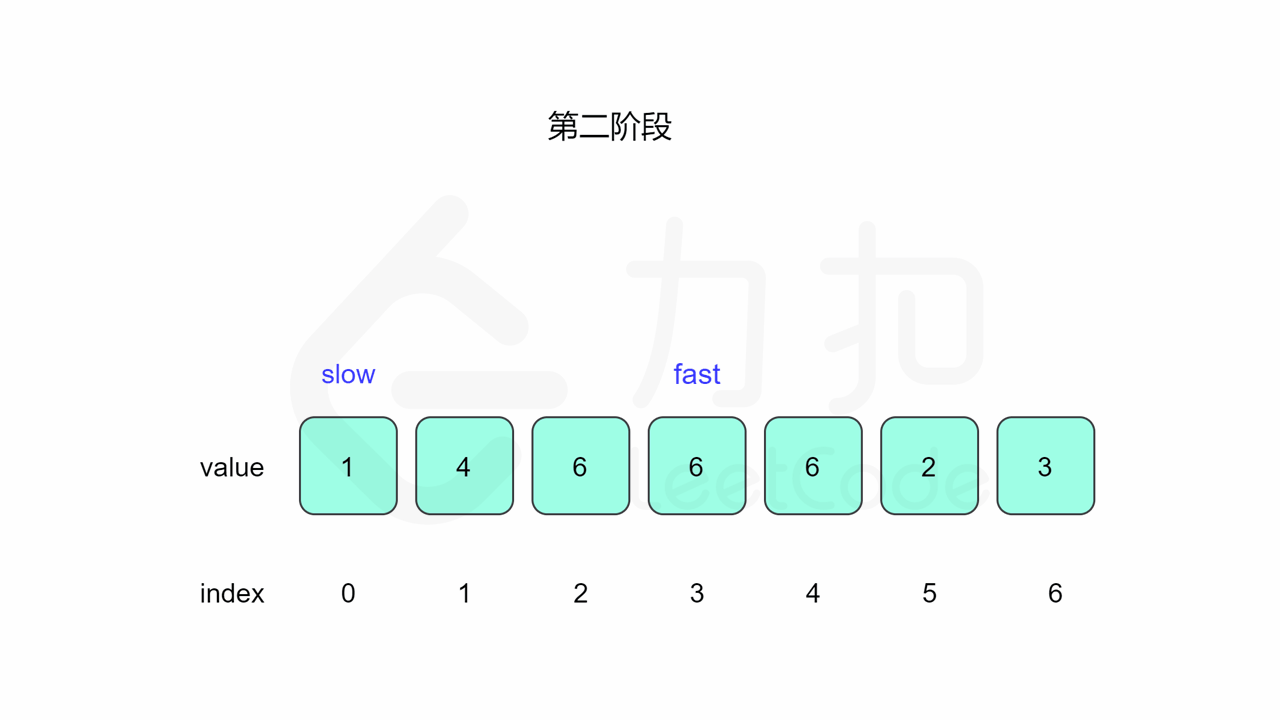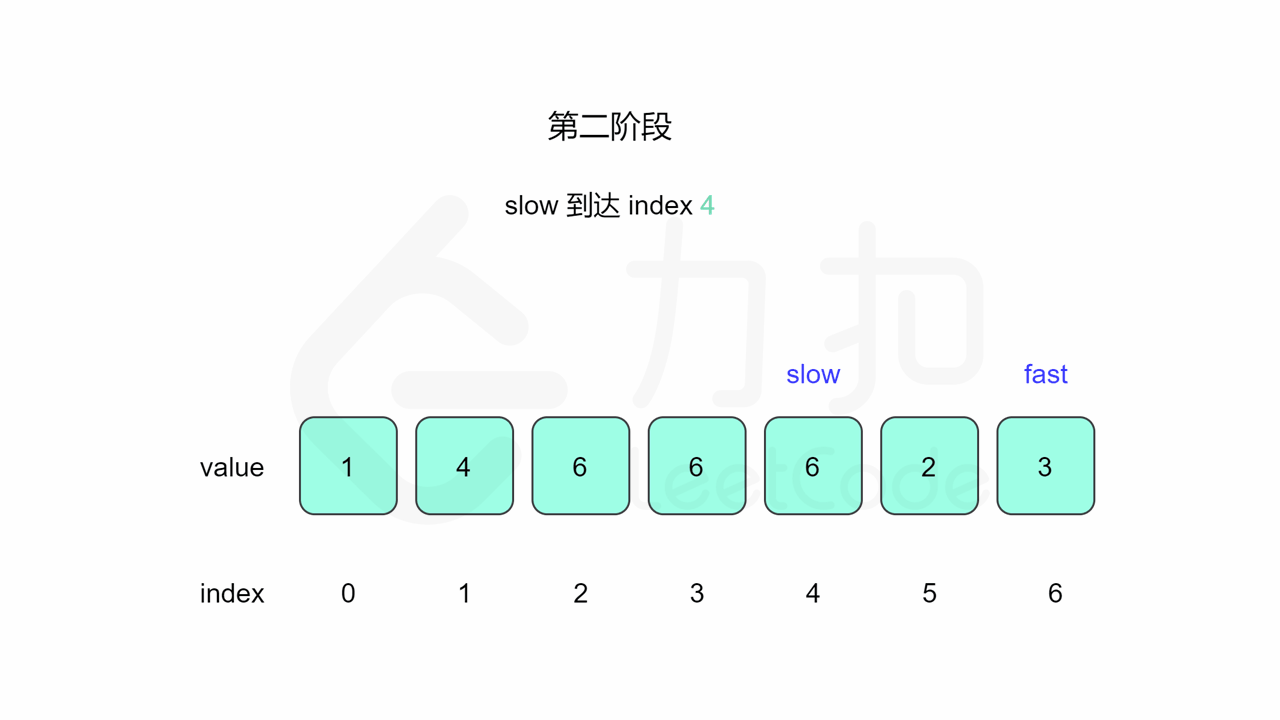
在示例1中的原数组【1,3,4,2,2】:
<=1 的数有几个啊 1个
<=2 的数有几个啊 3个
<=3 的数有几个啊 4个
<=4 的数有几个啊 5个
所以你看,是不是一个数越大,原数组中小于等于这个数就越多,我们记这个属性为cnt,则现在我们知道,对于【1,2,3,...n-1】这个数组值升序数组来说,数组的cnt属性值也是升序的。
接下来看看我们的目标值target,它的cnt属性有什么特点呢。因为它在原数组中是重复的,那就说明一点:target的cnt属性值是大于target的。继续举例来看:
脱离本题来说,一定有:
小于等于2的正数有2个:(1,2)
小于等于3的正数有3个:(1,2,3)
小于等于num的正数有num个:(1,2,3,...num)
.......
而如果允许num本身重复的话,则<=num的数的个数一定是>num的。(1,2,...num,num,num...)
根据这个特点,去看我们说的cnt属性,就容易得到target的cnt属性值是>target的。
综上,我们得到如下结论:
若num是【1,n-1】中的一个数,target是原数组中的重复值,则:
if num<target, num的cnt属性值<=num
if num>=target, num的cnt属性值>num
代码实现:
class Solution {
public int findDuplicate(int[] nums) {
int n = nums.length;
int l = 1, r = n - 1, ans = -1;
while (l <= r) {
int mid = (l + r) >> 1;
int cnt = 0;
for (int i = 0; i < n; ++i) {
if (nums[i] <= mid) {
cnt++;
}
}
if (cnt <= mid) {
l = mid + 1;
} else {
r = mid - 1;
ans = mid;
}
}
return ans;
}
}方法二:快慢指针
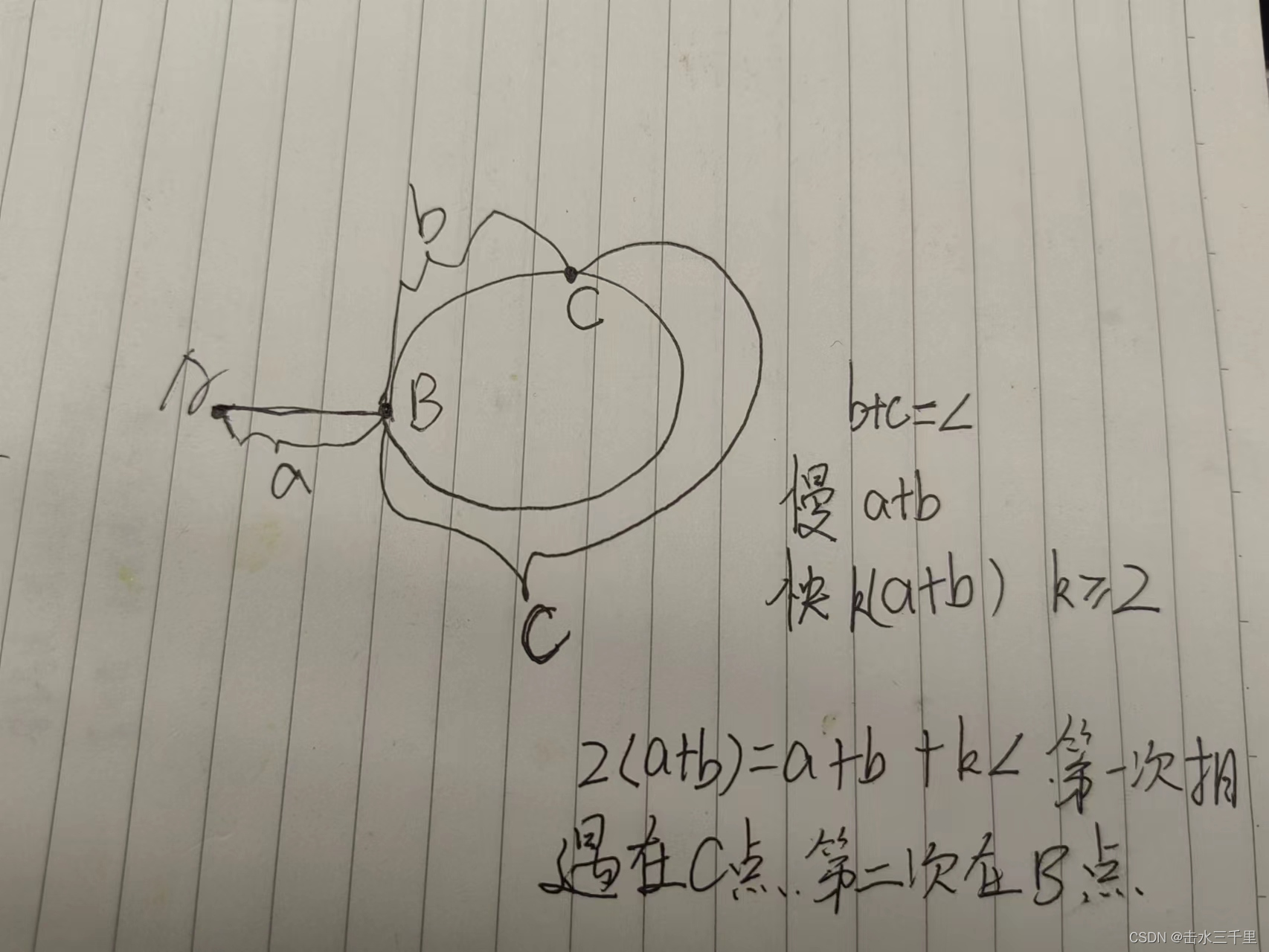
什么后面将 slow 放置起点后移动相遇的点就一定是答案了。假设环长为 L,从起点到环的入口的步数是 a,从环的入口继续走 b 步到达相遇位置,从相遇位置继续走 c 步回到环的入口,则有 b+c=L,其中 L、a、b、c 都是正整数。根据上述定义,慢指针走了 a+b 步,快指针走了 2(a+b) 步。从另一个角度考虑,在相遇位置,快指针比慢指针多走了若干圈,因此快指针走的步数还可以表示成 a+b+kL,其中 k表示快指针在环上走的圈数。联立等式,可以得到
2(a+b)=a+b+kL
class Solution {
public int findDuplicate(int[] nums) {
int slow = 0, fast = 0;
//第一次相遇在C点
do {
slow = nums[slow];
fast = nums[nums[fast]];
} while (slow != fast);
slow = 0;
//第二次相遇在B点
while (slow != fast) {
slow = nums[slow];
fast = nums[fast];
}
return slow;
}
}