题目描述
有 A 和 B 两种类型 的汤。一开始每种类型的汤有 n 毫升。有四种分配操作:
提供 100ml 的 汤A 和 0ml 的 汤B 。
提供 75ml 的 汤A 和 25ml 的 汤B 。
提供 50ml 的 汤A 和 50ml 的 汤B 。
提供 25ml 的 汤A 和 75ml 的 汤B 。
当我们把汤分配给某人之后,汤就没有了。每个回合,我们将从四种概率同为 0.25 的操作中进行分配选择。如果汤的剩余量不足以完成某次操作,我们将尽可能分配。当两种类型的汤都分配完时,停止操作。
注意 不存在先分配 100 ml 汤B 的操作。
需要返回的值: 汤A 先分配完的概率 + 汤A和汤B 同时分配完的概率 / 2。返回值在正确答案 10-5 的范围内将被认为是正确的。示例 1:
输入: n = 50
输出: 0.62500
解释:如果我们选择前两个操作,A 首先将变为空。
对于第三个操作,A 和 B 会同时变为空。
对于第四个操作,B 首先将变为空。
所以 A 变为空的总概率加上 A 和 B 同时变为空的概率的一半是 0.25 *(1 + 1 + 0.5 + 0)= 0.625。示例 2:
输入: n = 100
输出: 0.71875提示:
0 <= n <= 109
方法一:动态规划(自底向上)
class Solution {
public:
double soupServings(int n) {
// 如果n的值大等于4475,说明汤A肯定会先被分配完
if(n >= 4475) return 1.0;
// /25方便计算,ceil向上取整
n = ceil((double)n / 25);
// 定义动态规划数组dp
// dp[i][j]表示汤A和汤B分别剩余i和j时的概率值
vector<vector<double>> dp(n+1, vector<double>(n+1));
// dp[0][0]表示同时完成分配
dp[0][0] = 0.5;
// dp[0][j]表示汤A已经分配完,概率恒为1
for(int i=1; i<=n ; i++){
dp[0][i] = 1.0;
}
// 考虑剩下的情况,注意下标需要大于0,因此使用max函数来判断
for(int i=1; i<=n ;i++){
for(int j=1; j<=n; j++){
dp[i][j] = 0.25 * (dp[max(0, i - 4)][j] +
dp[max(0, i - 3)][max(0, j - 1)] +
dp[max(0, i - 2)][max(0, j - 2)] +
dp[max(0, i - 1)][max(0, j - 3)]);
}
}
return dp[n][n];
}
};
方法二:动态规划(自顶向下)
class Solution {
public:
double soupServings(int n) {
// 如果n的值大等于4475,说明汤A肯定会先被分配完
if(n >= 4475) return 1.0;
// /25方便计算,ceil向上取整
n = ceil((double)n / 25);
// 定义动态规划数组dp
// dp[i][j]表示汤A和汤B分别剩余i和j时的概率值
vector<vector<double>> dp(n+1, vector<double>(n+1));
// dp[n][n]表示汤A和汤B分别剩余n的概率为1
dp[n][n] = 1.0;
// 定义temp为当前dp[i][j]对于分布的四种情况的概率值
double temp = 0.0;
// 对所有蓝色块进行计算
for(int i=n; i>0; i--){
for(int j=n; j>0; j--){
// 汤B先被分配完,对最终结果没有影响
if(dp[i][j] == 0) continue;
temp = 0.25 * dp[i][j];
dp[max(0, i - 4)][j] += temp;
dp[max(0, i - 3)][max(0, j - 1)] += temp;
dp[max(0, i - 2)][max(0, j - 2)] += temp;
dp[max(0, i - 1)][max(0, j - 3)] += temp;
}
}
// 汤A和汤B同时分完,概率为0
dp[0][0] /= 2;
// 累加所有可能的情况
for(int i=1; i<=n; i++)
dp[0][0] += dp[0][i];
return dp[0][0];
}
};
方法三:DFS(自顶向下)
class Solution {
public:
double soupServings(int n) {
// 如果n的值大等于4475,说明汤A肯定会先被分配完
if(n >= 4475) return 1.0;
// /25方便计算,ceil向上取整
n = ceil((double)n / 25);
// 定义动态规划数组dp
// dp[i][j]表示汤A和汤B分别剩余i和j时的概率值
dp = vector<vector<double>>(n + 1, vector<double>(n + 1));
// vector<vector<double>> dp(n + 1, vector<double>(n + 1));
// 这种定义的方式会出错,可能因为dp是全局变量
return dfs(n, n);
}
// 记忆化搜索
double dfs(int a, int b){
if(a <= 0 && b <= 0) return 0.5; // 汤A和汤B都已经分配完
else if(a <= 0) return 1.0; // 汤A分配完
else if(b <= 0) return 0.0; // 汤B分配完
// df初始值为0
// 所有如果df > 0,则说明已经完成计算
if(dp[a][b] > 0) return dp[a][b];
// 计算df
dp[a][b] = 0.25 * (dfs(a - 4, b) +
dfs(a - 3, b - 1) +
dfs(a - 2, b- 2) +
dfs(a - 1, b - 3));
return dp[a][b];
}
private:
vector<vector<double>> dp;
};
心得
- 今天也没有自己做出来,有想到要用动态规划,但是具体操作还是不了解。
- 方法一:动态规划(自底向上)
由于四组容量都是25的倍数,因此四组操作可以简化为(4,0), (3,1), (2,2),(1,3),同时, n 也需要除以 25 。
明确dp[ i ][ j ] 的定义
假设 dp[i][j] 为汤 A 和汤 B 分别剩下 i ml 和 j ml时候的概率值。确定状态转移方程
dp [ i ] [ j ] = 0.25 * (dp [ i - 4 ][ j ] + dp [ i - 3 ][ j - 1 ] + dp [ i - 2 ][ j - 2 ] + dp [ i - 1 ][ j - 3 ])确定边界条件
- 当 i > 0, j = 0 时,此时 汤A 不可能先完成分配, 汤A 和 汤B 也不可能同时完成分配,因此概率值 P = 0;
- 当 i = 0 ,j = 0 时,此时 汤A 和 汤B 同时完成分配,因此概率值 P = 0 + 0.5 * 1 = 0.5;
- 当 i = 0 ,j > 0时,此时 汤A 已经先完成分配,因此概率值 P = 1.
综上所述,dp [ i ][ j ]的边界条件就有以上三种。
优化算法
此时,算法的时间复杂度为O(n2),当 n 特别大的时候,可能会TLE,因此需要进行优化,可以找出 n >= 4475 时,概率值已经接近1,此时可以直接给出答案不必判断。
那么4475如何得出呢?
首先我们先计算出 汤A 每次分配的平均期望为 E(A) = (4 + 3 + 2 + 1)/ 4 = 2.5,
汤B 每次分配的平均期望为 E(B) = (0 + 1 + 2 +3) / 4 = 1.5,因此当n足够大的时候,A肯定会先被分完。由于题目给出了误差值为10-5 ,也就是说当答案 > 0.99999 的时候,可以直接返回1 。
可以通过运行上面代码寻找到这个值,为4475。
- 方法二:动态规划(自顶向下)
自底向上的方法会计算很多无用的值,而自顶向下的动态规划则会避免多余的计算。
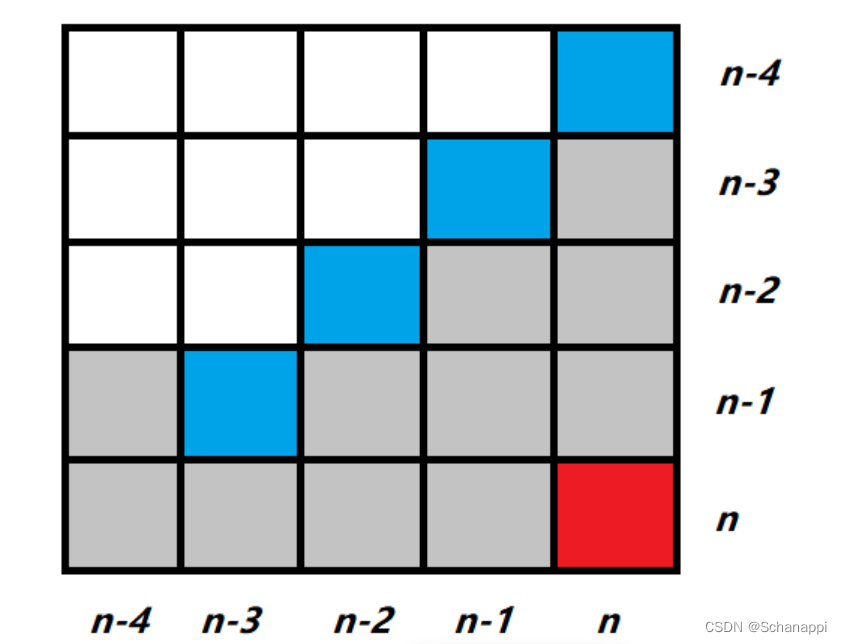
如图,红色块是最终要求得的值,那么需要通过蓝色块得到红色块,灰色块都是无用的值。
- 从 dp[ n ][ n ]开始,自顶向下依次递推:
- dp[ n ][ n ],它出现的概率为1,这是既定事实;
- 确定状态转移方程
dp[ n ][ n ]进行四次分布后,每种情况的出现概率都为0.25,再一次进行分布也是一样的,因此,得到状态转移方程:
dp[ a - 4 ][ b ] = 0.25 * dp[ a ][ b ]
dp[ a - 3 ][ b - 1 ] = 0.25 * dp[ a ][ b ]
dp[ a - 2 ][ b - 2 ] = 0.25 * dp[ a ][ b ]
dp[ a - 3 ][ b - 1 ] = 0.25 * dp[ a ][ b ]- 确定边界条件,计算最终结果
最终结果 = 汤A 先分完的概率 + 汤A 和 汤B 同时分完的概率
- 汤A 先分完的概率 = dp[ 0 ][ j ] ,其中 j != 0 且 j <= n;
- 汤A 和 汤B 同时分完的概率 = dp[ 0 ][ 0 ]
- 方法三:dfs记忆化搜索(自顶向下)
这个方法的思路和方法二差不多,也是为了避免无效块的计算。
- 总结
- 自底向上的方式(方法一)
先给最底层(边界)情况赋贡献值,然后向上推出上一层情况对答案的贡献值,以此类推,最终得到答案- 自顶向下的方式(方法二,三)
从最开始的情况计算,向下推出下一层情况的真实发生概率,以此类推,直到所有分支情况到达边界,最终将边界情况的真实概率进行总结计算
参考资料:
[1]优秀题解
[2]深度优先搜索之记忆化dfs








![PTA题目 计算分段函数[1]](https://img-blog.csdnimg.cn/661aa64181584fdfa0c56ecbdc51a336.png)
