wy的leetcode刷题记录_Day46

声明

本文章的所有题目信息都来源于leetcode
如有侵权请联系我删掉!
时间：2022-11-19

前言

补

1732. 找到最高海拔

今天的每日一题是：1732. 找到最高海拔

题目介绍

有一个自行车手打算进行一场公路骑行，这条路线总共由 n + 1 个不同海拔的点组成。自行车手从海拔为 0 的点 0 开始骑行。

给你一个长度为 n 的整数数组 gain ，其中 gain[i] 是点 i 和点 i + 1 的净海拔高度差（0 <= i < n）。请你返回最高点的海拔。

示例 1：
输入：gain = [-5,1,5,0,-7]
输出：1
解释：海拔高度依次为 [0,-5,-4,1,1,-6] 。最高海拔为1 。

示例 2：
输入：gain = [-4,-3,-2,-1,4,3,2]
输出：0
解释：海拔高度依次为[0,-4,-7,-9,-10,-6,-3,-1] 。最高海拔为 0 。

思路

方法一：贪心算法+模拟：
题目给出的数组为高度差，那么我们遍历这个高度差然后从海拔0开始叠加每一次迭代得到当前的海拔高度，维护一个最高海拔遍历就可以了。（一次遍历+一个变量）
方法二：前缀和：
遍历题目的高度差数组，将其变为前缀和，这样就得到了每一处的海拔高度，然后寻找其中的最大值就可以了。（这样好像还是复杂一些）（俩次遍历+无额外空间）

代码

贪心模拟：

class Solution {
public:
    int largestAltitude(vector<int>& gain) {
        int ans = 0, sum = 0;
        for (int x: gain) {
            sum += x;
            ans = max(ans, sum);
        }
        return ans;
    }
};

前缀和：

class Solution {
public:
    int largestAltitude(vector<int>& gain) {
        int n=gain.size();
        for(int i=1;i<n;i++)
        {
            gain[i]+=gain[i-1];
        }
        return max(*max_element(gain.begin(),gain.end()),0); 
    }
};

收获

很简单的一题没有什么收获说实话，手速题吧。

106. 从中序与后序遍历序列构造二叉树

题目介绍

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗二叉树。

示例 1:

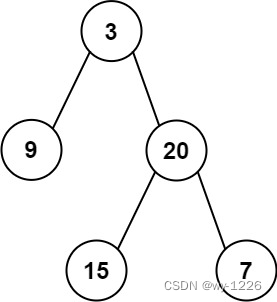
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:
输入：inorder = [-1], postorder = [-1]
输出：[-1]

思路

首先我们知道中序遍历的顺序是左中右，后续遍历的顺序是左右中。并且在后序遍历序列中的最后一个元素就是根节点，我们根据此根节点在中序遍历序列中同样找到根节点。并且又知在中序遍历序列中的根节点左边的节点就是左子树，右边的节点就是右子树。所以依次我们根据这个序列将树分为俩颗子树，再将中序遍历序列和后续遍历序列分别切割为中序左遍历序列、中序右遍历序列、后续左遍历序列、后续右遍历序列，这样递归，直到只剩一个节点的时候就是叶子节点，以此来构建树。

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if(inorder.size()==0||postorder.size()==0)
            return nullptr;
        return travel(inorder,postorder);
    }
    
    TreeNode* travel(vector<int>& inorder, vector<int>& postorder)
    {
        if(postorder.size()==0)
            return nullptr;
        //寻找分割点 后续数组的最后一个
        int rootVal=postorder[postorder.size()-1];
        TreeNode* root=new TreeNode(rootVal);
        
        if(postorder.size()==1)
            return root;
        
        //寻找中序遍历的切割点
        int SplitIndex=0;
        for(;SplitIndex<inorder.size();SplitIndex++)
        {
            if(inorder[SplitIndex]==rootVal)
                break;
        }
        //切割中序数组
        vector<int> leftInorder(inorder.begin(),inorder.begin()+SplitIndex);
        vector<int> RightInorder(inorder.begin()+SplitIndex+1,inorder.end());//跳过该root节点

        //舍弃后续数组的最后一个元素
        postorder.resize(postorder.size()-1);

        //切割后续数组 只要求长度与中序数组切割后的一致就ok
        vector<int> leftPostorder(postorder.begin(),postorder.begin()+SplitIndex);
        vector<int> RightPostorder(postorder.begin()+SplitIndex,postorder.end());//之前舍弃节点的时候跳过该root节点
        root->left=travel(leftInorder,leftPostorder);
        root->right=travel(RightInorder,RightPostorder);
        return root;
        

        

    }
};