双端队列BFS
在最基本的广度优先搜索中,每次沿着分支的扩展都记为“一步”,我们通过逐层搜索,解决了求从起始状态到每个状态的最少步数的问题。这其实等价于在一张边权均为1的图上执行广度优先遍历,求出每个点相对于起点的最短距离(层次)。在第0x21节中我们曾讨论过这个问题,并得到了“队列中的状态的层数满足两段性和单调性”的结论,从而我们可以知道,每个状态在第一次被访问并入队时,计算出的步数即为所求。
然而,如果图上的边权不全是1呢?换句话说,如果每次扩展都有各自不同的“代价“,我们想求出起始状态到每个状态的最小代价,应该怎么办呢?我们不妨先讨论图上的边权要么是1、要么是0的情况。
1、AcWing 175. 电路维修
题意 :
- 电路板的整体结构是一个 R 行 C 列的网格(R,C≤500),如下图所示。
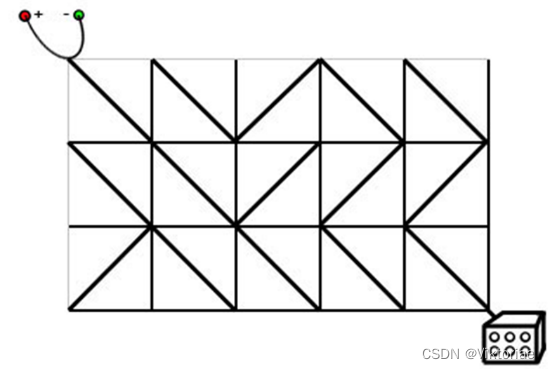
- 每个格点都是电线的接点,每个格子都包含一个电子元件。
- 电子元件的主要部分是一个可旋转的、连接一条对角线上的两个接点的短电缆。
- 在旋转之后,它就可以连接另一条对角线的两个接点。
- 电路板左上角的接点接入直流电源,右下角的接点接入飞行车的发动装置。
- 达达发现因为某些元件的方向不小心发生了改变,电路板可能处于断路的状态。
- 她准备通过计算,旋转最少数量的元件,使电源与发动装置通过若干条短缆相连。
- 1≤T≤5
转义:

思路 :
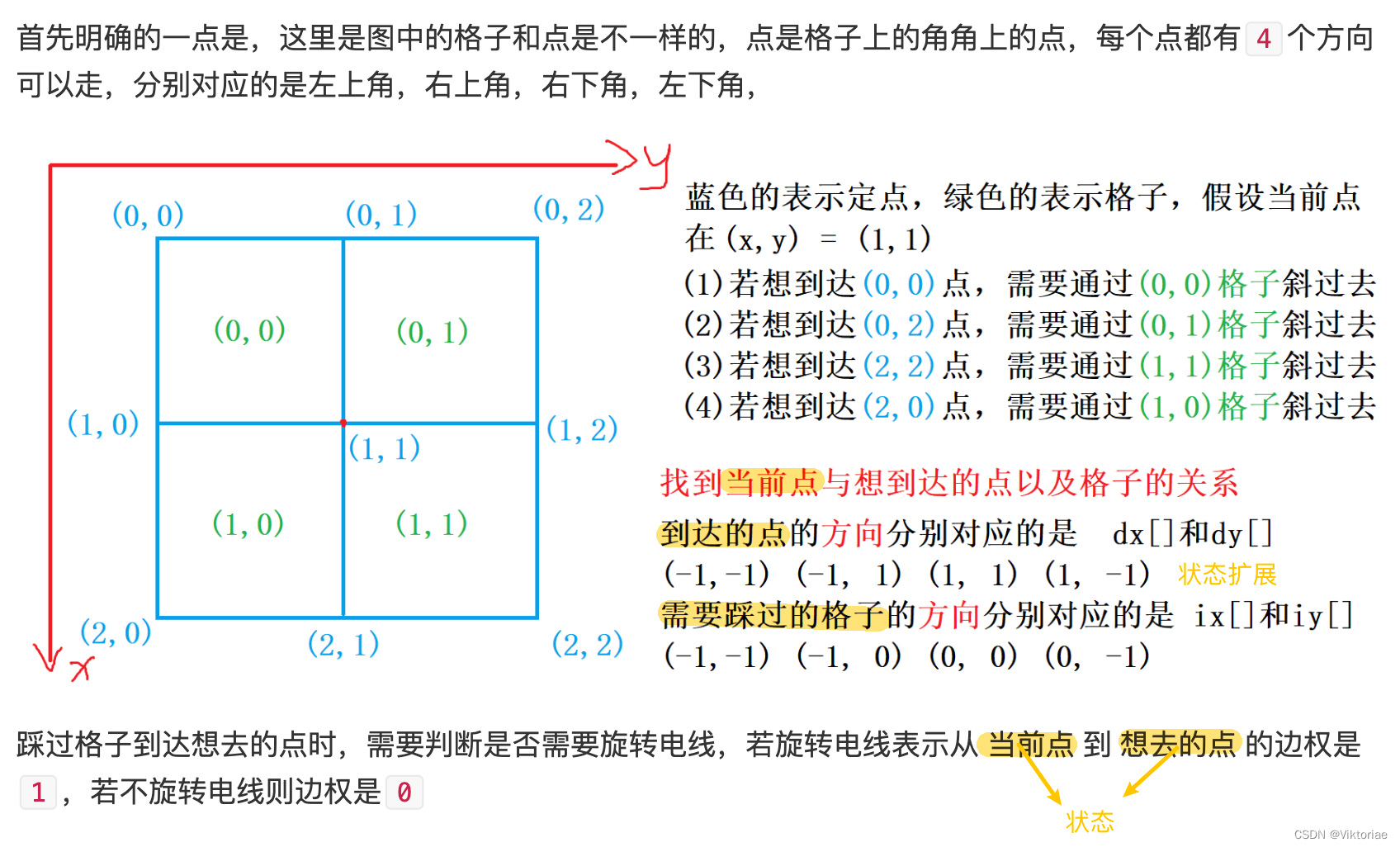
- 我们可以把电路板上的每个格点(横线与竖线的交叉点)看作无向图中的节点。若两个节点x和y是某个小方格的两个对焦,则在x与y之间连边。若该方格中的标准件(对角线)与x到y的线段重合,则边权为0;若垂直相交,则边权为1(说明需要旋转1次才能连上)。然后,我们在这个无向图中求出左上角到右下角的最短距离,就得到了答案。
- 这是一张边权要么是0、要么是1的无向图。在这样的图上,我们可以通过双端队列广搜来计算。算法的整体框架与一般的广搜类似,只是在每个节点上沿分支扩展时稍作改变。如果这条分支是边权为0的边,就把沿该分支到达的新节点从队头入队;如果这条分支是边权为1的边,就像一般的广搜一样从队尾入队。这样一来,我们就仍然能保证,任意时刻广搜队列中的节点对应的距离值都具有“两段性”和“单调性”,每个节点虽然可能被更新(入队)多次,但是它第一次被扩展(出队)时,就能得到从左上角到该节点的最短距离,之后再被取出可以直接忽略,时间复杂度为 O ( R ∗ C ) O(R*C) O(R∗C)
- 每个点虽然可能入队多次,但第一次出来的时候就已经取到最小值了(dijkstra算法的性质),因此后面重复出队的点应该直接忽略。当忽略重复出队的点后,就能保证每个点只会更新其他点一次,从而总共更新的次数等于总边数,这样时间复杂度就能保证是 O(RC)了
#include <iostream>
#include <cstring>
#include <deque>
using namespace std;
typedef pair<int, int> PII;
const int N = 510;
int n, m;
char g[N][N];
bool st[N][N];
int dist[N][N];
int bfs() {
deque<PII> que;
que.push_back({0, 0});
dist[0][0] = 0;
int dx[] = {1, -1, -1, 1}, dy[] = {1, 1, -1, -1};
int ix[] = {0, -1, -1, 0}, iy[] = {0, 0, -1, -1};
char cs[] = "\\/\\/";
while (que.size()) {
PII t = que.front(); que.pop_front();
int x = t.first, y = t.second;
if (x == n && y == m) return dist[x][y];
if (st[x][y]) continue;
st[x][y] = true;
for (int i = 0; i < 4; ++ i) {
int a = x + dx[i], b = y + dy[i];
int j = x + ix[i], k = y + iy[i];
if (a >= 0 && a <= n && b >= 0 && b <= m) {
int w = 0;
if (g[j][k] != cs[i]) w = 1;
if (dist[x][y] + w < dist[a][b]) {
dist[a][b] = dist[x][y] + w;
if (w) que.push_back({a, b});
else que.push_front({a, b});
}
}
}
}
return -1;
}
int main() {
int _; scanf("%d", &_);
while (_ -- ) {
scanf("%d%d", &n, &m);
for (int i = 0; i < n; ++ i) scanf("%s", g[i]);
memset(st, 0, sizeof st);
memset(dist, 0x3f, sizeof dist);
int t = bfs();
if (t == -1) puts("NO SOLUTION");
else printf("%d\n", t);
}
}
优先队列BFS
对于更加具有普适性的情况,也就是每次扩展都有各自不同的代价时,求出起始状态到每个状态的最小代价,就相当于在一张带权图上求出从起点到每个节点的最短路。此时,我们有两个解决方案:
方法一:
- 仍然使用一般的广搜,采用一般的队列
- 这是我们不再能保证每个状态第一次入队时就能得到最小代价,所以只能允许一个状态被多次更新、多次进出队列。我们不断执行搜索,直到队列为空
- 整个广搜算法对搜索树进行了重复遍历与更新,直至“收敛”到最优解,其实也就是“迭代”的思想。最坏情况下,该算法的时间复杂度会从一般广搜的
O
(
N
)
O(N)
O(N)增长到
O
(
N
2
)
O(N^2)
O(N2)。对应在最短路问题中,就是我们将在0x61节介绍的
SPFA算法
方法二:
- 改用优先队列进行广搜
- 这里的“优先队列”就相当于一个二叉堆。我们可以每次从队列中取出当前代价最小的状态进行扩展(该状态一定已经是最优的,因为队列中其他状态的当前代价都不小于它,所以以后都不可能再更新它了),沿着各条分支到达的新状态加入优先队列。不断执行搜索,知道队列为空
- 在优先队列BFS中,每个状态也会被多次更新、多次进出队列,一个状态也可能以不同的代价在队列中同时存在。不过,当每个状态第一次从队列中被取出时,就得到了起始状态到当前状态的最小代价。之后若再被取出,则可以直接忽略,不进行扩展。所以,优先队列BFS中每个状态只扩展一次,时间复杂度只多了维护二叉堆的代价。若一般广搜复杂度为
O
(
N
)
O(N)
O(N),则优先队列BFS的复杂度为
O
(
N
l
o
g
N
)
O(NlogN)
O(NlogN)。对应在最短路问题中,就是我们将在0x61节介绍的堆优化的
Dijkstra算法
至此,我们就可以对BFS的形式,按照对应在图上的边权情况进行分类总结:

1、AcWing 176. 装满的油箱
题意 :
- 有 N 个城市(编号 0、1…N−1)和 M 条道路,构成一张无向图。
- 在每个城市里边都有一个加油站,不同的加油站的单位油价不一样。
- 现在你需要回答不超过 100 个问题,在每个问题中,请计算出一架油箱容量为 C 的车子,从起点城市 S 开到终点城市 E 至少要花多少油钱?
- 1≤N≤1000,
- 1≤M≤10000,
思路 :
- 我们使用二元组(city, fuel)来表示每个状态,其中city为城市编号,fuel为油箱中剩余的汽油量,并使用记录数组d[city][fuel]存储最少花费。
- 对于每个问题,我们都单独进行一次优先队列BFS。起始状态为(S, 0)。每个状态(city, fuel)的分支有:
1、若fuel < C,可以加1升油,扩展到新状态(city, fuel + 1),花费在城市city加1升油的钱
2、对于每条从city出发的边(city, next),若边权大小w不超过fuel,可以开车前往城市next,扩展到新状态(next, fuel - w) - 我们不断取出优先队列中“当前花费最少”的状态(堆顶)进行扩展,更新扩展到的新状态在记录数组d中存储的值,直到终点T的某个状态第一次被取出,即可停止BFS,输出答案。
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
const int N = 1e3 + 10, M = 2e4 + 10, C = 110;
struct Ver {
int d, u, c;
bool operator< (const Ver&w) const {
return d > w.d;
}
};
int n, m;
int prices[N];
int e[M], ne[M], w[M], h[N], idx;
bool st[N][C];
int dist[N][C];
void add(int a, int b, int c) {
e[idx] = b; w[idx] = c; ne[idx] = h[a]; h[a] = idx ++ ;
}
int dijkstra(int start, int end, int cap) {
memset(st, 0, sizeof st);
memset(dist, 0x3f, sizeof dist);
priority_queue<Ver> pq;
pq.push({0, start, 0});
dist[start][0] = 0;
while (pq.size()) {
Ver t = pq.top(); pq.pop();
if (t.u == end) return dist[t.u][t.c];
if (st[t.u][t.c]) continue;
st[t.u][t.c] = true;
if (t.c < cap) {
if (dist[t.u][t.c + 1] > prices[t.u] + dist[t.u][t.c]) {
dist[t.u][t.c + 1] = prices[t.u] + dist[t.u][t.c];
pq.push({dist[t.u][t.c + 1], t.u, t.c + 1});
}
}
for (int i = h[t.u]; ~i; i = ne[i]) {
int j = e[i];
// cout << j << endl;
if (t.c >= w[i]) {
if (dist[j][t.c - w[i]] > dist[t.u][t.c]) {
dist[j][t.c - w[i]] = dist[t.u][t.c];
pq.push({dist[j][t.c - w[i]], j, t.c - w[i]});
}
}
}
}
return -1;
}
int main() {
memset(h, -1, sizeof h);
scanf("%d%d", &n, &m);
for (int i = 0; i < n; ++ i) scanf("%d", &prices[i]);
for (int i = 0; i < m; ++ i) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c); add(b, a, c);
}
int q;
scanf("%d", &q);
while (q -- ) {
int a, b, c;
scanf("%d%d%d", &c, &a, &b);
int t = dijkstra(a, b, c);
if (t == -1) puts("impossible");
else printf("%d\n", t);
}
}
双向BFS
在0x24节我们介绍了双向搜索的思想,并讲解了一道双向DFS的例题,双向BFS的思想与之完全相同,我们就不再重复描述。因为BFS本身就是逐层搜索的算法,所以双向BFS的实现更加自然、简便。以普通的求最少步数的双向BFS为例,我们只需从起始状态、目标状态分别开始,两边轮流进行,每次各扩展一整层。当两边各自有一个状态在记录数组中发生重复时,就说明这两个搜索过程相遇了,可以合并得出起点到终点的最少步数。
1、AcWing 177. 噩梦
题意 :
- 给定一张 N×M 的地图,地图中有 1 个男孩,1 个女孩和 2 个鬼。
- 字符 . 表示道路,字符 X 表示墙,字符 M 表示男孩的位置,字符 G 表示女孩的位置,字符 Z 表示鬼的位置。
- 男孩每秒可以移动 3 个单位距离,女孩每秒可以移动 1 个单位距离,男孩和女孩只能朝上下左右四个方向移动。
- 每个鬼占据的区域每秒可以向四周扩张 2 个单位距离,并且无视墙的阻挡,也就是在第 k 秒后所有与鬼的曼哈顿距离不超过 2k 的位置都会被鬼占领。
- 注意: 每一秒鬼会先扩展,扩展完毕后男孩和女孩才可以移动。
- 求在不进入鬼的占领区的前提下,男孩和女孩能否会合,若能会合,求出最短会合时间。
- 1<n,m<800
思路 :
- 使用双向BFS算法。建立两个队列,分别从男孩的初始位置、女孩的初始位置开始进行BFS,两边轮流进行
- 在每一轮中,男孩这边BFS三层(可以移动三步),女孩这边BFS一层(可以移动一步),使用数组d记录每个位置对于男孩和女孩的可达性
- 当然,在BFS的每次扩展时,注意实时计算新状态与鬼之间的曼哈顿距离,如果已经小于等于当前轮数(即秒数)的2倍,那么就判定这个新状态不合法,不再记录或入队
- 在BFS的过程中,第一次出现某个位置(x, y)即能被男孩到达,也能被女孩到达时,当前轮数就是两人的最短相会时间
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 810;
int n, m;
char g[N][N];
int st[N][N];
PII boy, girl;
PII ghost[2];
bool check(int x, int y, int step) {
if (x < 0 || x >= n || y < 0 || y >= m || g[x][y] == 'X' || g[x][y] == 'Z') return false;
for (int i = 0; i < 2; ++ i) {
if (abs(x - ghost[i].first) + abs(y - ghost[i].second) <= 2 * step)
return false;
}
return true;
}
int bfs() {
memset(st, 0, sizeof st);
int cnt = 0;
int dx[] = {1, 0, -1, 0}, dy[] = {0, 1, 0, -1};
for (int i = 0; i < n; ++ i) {
for (int j = 0; j < m; ++ j) {
if (g[i][j] == 'M') boy = {i, j};
else if (g[i][j] == 'G') girl = {i, j};
else if (g[i][j] == 'Z') ghost[cnt ++ ] = {i, j};
}
}
queue<PII> qb, qg;
qb.push(boy);
qg.push(girl);
int step = 0;
while (qb.size() || qg.size()) {
++ step;
for (int i = 0; i < 3; ++ i) {
for (int j = 0, len = qb.size(); j < len; ++ j) {
PII t = qb.front(); qb.pop();
int x = t.first, y = t.second;
if (!check(x, y, step)) continue;
for (int k = 0; k < 4; ++ k) {
int a = x + dx[k], b = y + dy[k];
if (!check(a, b, step)) continue;
if (st[a][b] == 2) return step;
if (!st[a][b]) {
st[a][b] = 1;
qb.push({a, b});
}
}
}
}
for (int i = 0; i < 1; ++ i) {
for (int j = 0, len = qg.size(); j < len; ++ j) {
PII t = qg.front(); qg.pop();
int x = t.first, y = t.second;
if (!check(x, y, step)) continue;
for (int k = 0; k < 4; ++ k) {
int a = x + dx[k], b = y + dy[k];
if (!check(a, b, step)) continue;
if (st[a][b] == 1) return step;
if (!st[a][b]) {
st[a][b] = 2;
qg.push({a, b});
}
}
}
}
}
return -1;
}
int main() {
int _; scanf("%d", &_);
while (_ -- ) {
scanf("%d%d", &n, &m);
for (int i = 0; i < n; ++ i) scanf("%s", g[i]);
printf("%d\n", bfs());
}
}