题目：
799. 香槟塔
个人总结
799. 香槟
我们把玻璃杯摆成金字塔的形状，其中 第一层 有
1个玻璃杯， 第二层 有2个，依次类推到第 100 层，每个玻璃杯 (250ml) 将盛有香槟。从顶层的第一个玻璃杯开始倾倒一些香槟，当顶层的杯子满了，任何溢出的香槟都会立刻等流量的流向左右两侧的玻璃杯。当左右两边的杯子也满了，就会等流量的流向它们左右两边的杯子，依次类推。（当最底层的玻璃杯满了，香槟会流到地板上）
例如，在倾倒一杯香槟后，最顶层的玻璃杯满了。倾倒了两杯香槟后，第二层的两个玻璃杯各自盛放一半的香槟。在倒三杯香槟后，第二层的香槟满了 - 此时总共有三个满的玻璃杯。在倒第四杯后，第三层中间的玻璃杯盛放了一半的香槟，他两边的玻璃杯各自盛放了四分之一的香槟，如下图所示。
个人误区：
一开始觉得直接使用数学方法计算就好了，就计算每一层的体积，然后用倒入的总杯数减取就可以了，这种方式在结果只有0或1的时候的可以的，因为不需要精确，当你需要景区的时候，你会发现你的结果是错误的。最最主要是没有理解题目的流法。
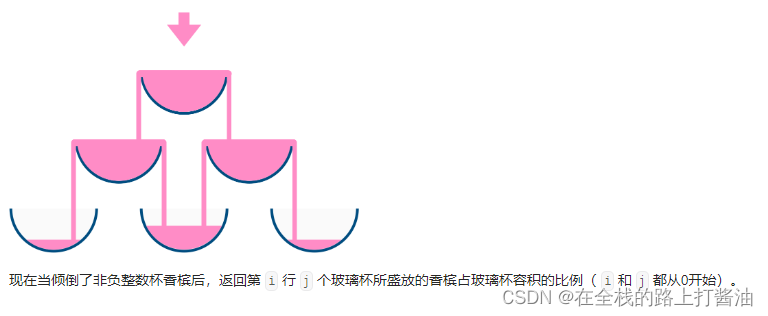如上图，在第三排，如果中间那个杯子满的话，旁边的两个是还没有满的，这个时候其实并不能使用数学方式去推算规律，然后去运算的。因为你不知道上面的杯子到底会流多少下来，在最后最边边的杯子也不一样是符合数学规律的。因为中间的流的比两边的块，也就存在可能中间满了，两边没满，然后中间的往下面流。
解决方法：
使用模拟法，就是去模拟每个杯子会经过多少。
我接了多少。会都流到下面多少。一层一层模拟。
也就是说，下面两个杯子的量取决于上面那个杯子流多少。
class Solution {
public double champagneTower(int poured, int query_row, int query_glass) {
double[] table = {poured}; // 设置了头顶的值，第一杯
for(int i = 1; i <= query_row; i++){
double[] quer = new double[i+1];
for(int j = 0; j < i; j++){
double volume = table[j];
if(volume > 1){
quer[j] += (volume-1)/2;
quer[j+1] += (volume-1)/2;
}
}
table = quer;
}
return Math.min(1, table[query_glass]);
}
}有另一种使用二维数组计算的
class Solution {
public double champagneTower(int poured, int query_row, int query_glass) {
double[][] table = new double[query_row+5][query_row+5];
table[0][0] = poured;
for(int i = 0; i <= query_row; i++){
for(int j = 0; j <= i; j++){
// 一开始这里没有使用等于导致结果错误，因为如果不等于的话，每一行就少了一杯，比如1的时候是第二行，小于1 就第二行只有一杯了
if(table[i][j] > 1){
table[i+1][j] += (table[i][j] - 1)/2;
table[i+1][j+1] += (table[i][j] - 1)/2;
}
}
}
return Math.min(table[query_row][query_glass],1);
}
}觉得这种题还有一个十分困惑的地方就是下标，因为
query_glass题目中说明了是从0开始的，这点还是需要注意的
