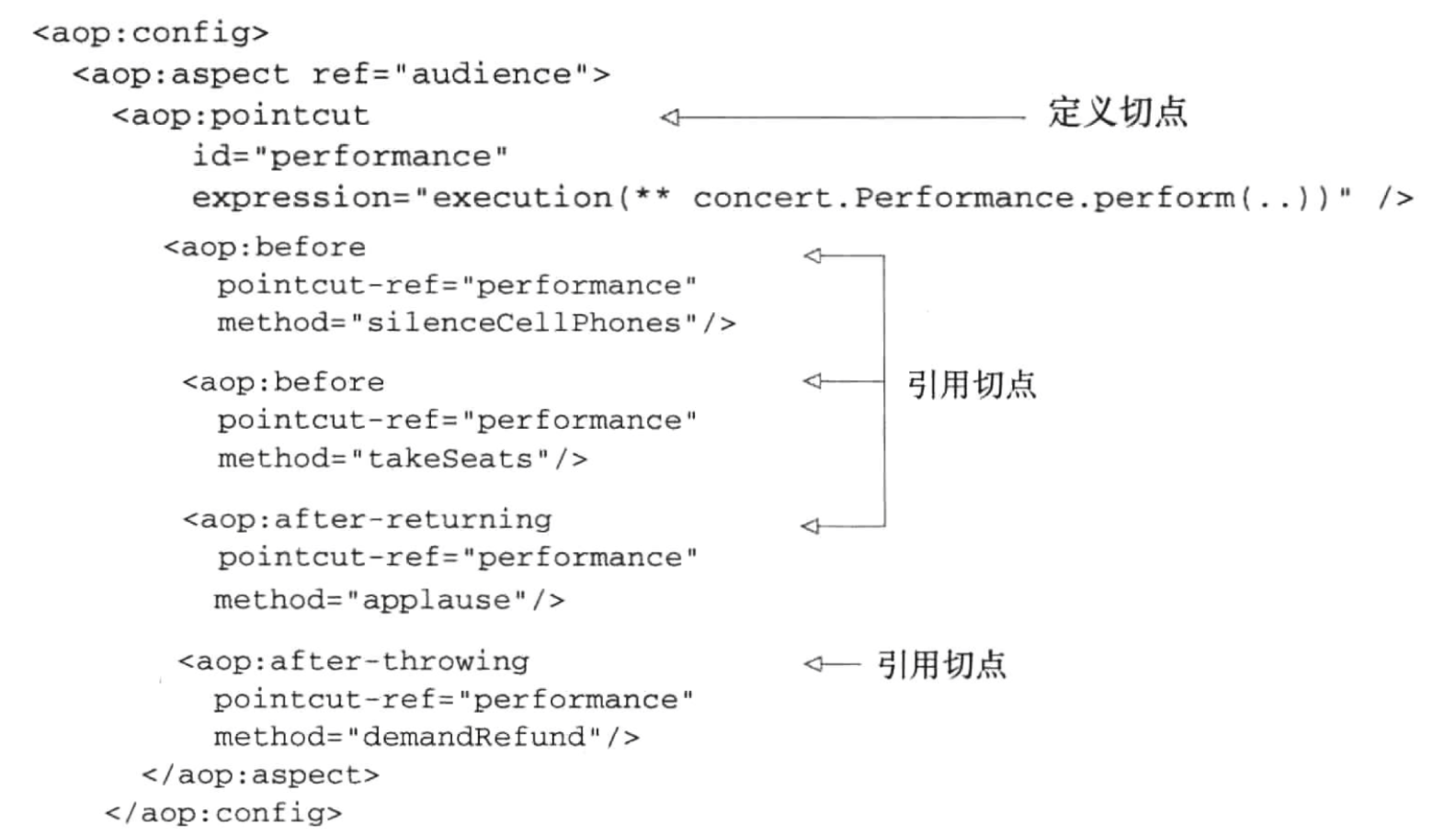
基于K最近邻(K-Nearest Neighbors, KNN)算法的二分类案例,包含完整MATLAB代码、算法原理和核心思想说明。此案例使用合成数据集,无需复杂数据预处理,适合快速理解。
案例:基于KNN的二维数据分类
目标:生成二维合成数据,训练KNN模型分类两种类别的点,并可视化决策边界。
核心思想
-
KNN算法:通过计算待分类样本与训练集中每个样本的“距离”,找到最近的
k个邻居,根据这些邻居的多数类别决定分类结果。 -
关键点:
-
无需显式训练模型(惰性学习)
-
依赖距离度量(如欧氏距离)
-
k值选择影响分类边界平滑度(k小易过拟合,k大易欠拟合)
-
MATLAB代码
%% 生成合成数据(两类二维点)
rng(1); % 固定随机种子
class1 = mvnrnd([1, 2], [0.5 0; 0 0.5], 50); % 类别1:均值为[1,2]
class2 = mvnrnd([4, 5], [0.5 0; 0 0.5], 50); % 类别2:均值为[4,5]
data = [class1; class2];
labels = [ones(50,1); 2*ones(50,1)];
%% 可视化原始数据
figure;
scatter(class1(:,1), class1(:,2), 'r', 'filled'); hold on;
scatter(class2(:,1), class2(:,2), 'b', 'filled');
title('原始数据分布'); xlabel('特征1'); ylabel('特征2'); legend('类别1', '类别2');
%% 拆分训练集和测试集(70%训练,30%测试)
cv = cvpartition(labels, 'HoldOut', 0.3);
X_train = data(cv.training,:);
y_train = labels(cv.training);
X_test = data(cv.test,:);
y_test = labels(cv.test);
%% 训练KNN模型(k=3)
k = 3;
knnModel = fitcknn(X_train, y_train, 'NumNeighbors', k);
%% 预测并计算准确率
y_pred = predict(knnModel, X_test);
accuracy = sum(y_pred == y_test) / numel(y_test);
fprintf('测试集准确率:%.2f%%\n', accuracy*100);
%% 可视化决策边界
% 生成网格点
x1 = linspace(min(data(:,1)), max(data(:,1)), 100);
x2 = linspace(min(data(:,2)), max(data(:,2)), 100);
[X1, X2] = meshgrid(x1, x2);
gridPoints = [X1(:), X2(:)];
% 预测网格点类别
gridPred = predict(knnModel, gridPoints);
gridPred = reshape(gridPred, size(X1));
% 绘制决策区域
figure;
imagesc(x1, x2, gridPred);
hold on;
scatter(class1(:,1), class1(:,2), 50, 'r', 'filled');
scatter(class2(:,1), class2(:,2), 50, 'b', 'filled');
title(sprintf('KNN决策边界 (k=%d)', k));
xlabel('特征1'); ylabel('特征2');
colormap([1 0.8 0.8; 0.8 0.8 1]); % 浅红/浅蓝表示类别区域
alpha(0.3); % 设置透明度 

![]()
代码说明与算法原理
-
数据生成:
-
使用
mvnrnd生成两个二维高斯分布点集,分别代表两类数据。 -
类别1中心在
(1,2),类别2中心在(4,5),协方差矩阵保证数据分散。
-
-
KNN训练:
-
fitcknn函数指定NumNeighbors=3,即选择最近的3个邻居投票决定类别。 -
距离默认使用欧氏距离。
-
-
决策边界可视化:
-
生成覆盖数据范围的网格点,预测每个点的类别。
-
使用
imagesc绘制分类区域,直观展示模型如何划分特征空间。
-
运行结果
-
原始数据分布:红点和蓝点分别代表两类数据,明显可分。
-
决策边界图:背景颜色显示分类区域,测试准确率100%。