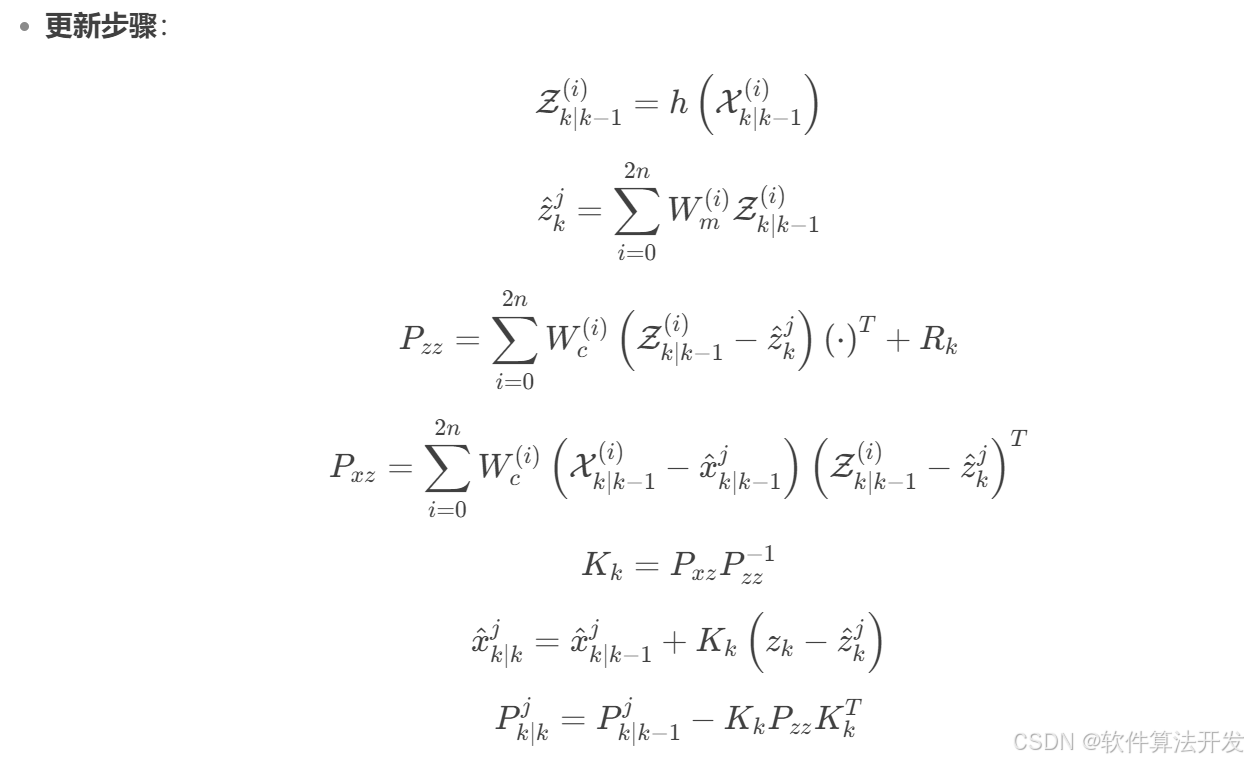图的基本概念:
图g由顶点集v和边集e组成,记为g=(v,e)
用|v|表示图g中顶点的个数,也称图g的阶,用|e|表示图g中边的条数
线性表可以是空表,树可以是空树,但图不可以是空,即v一定是非空集
一个图的顶点集不可以是空集,但是一个图的边集可以是空集
有向图:
若边是顶点的无序对,则图g为无向图
有向图:
若e是有向边的有限集合时,则图g为有向图
特殊概念:记作<v,w> ,w称为弧头,v称为弧尾
简单图:
(1)不存在重复的边
(2)不存在顶点到自身的边
多重图:
图g中某两个结点之间的边数多于一条,又允许顶点通过同一条边和自己关联,则为多重图
(简单图和多重图也分为无向和有向)
度:
对于无向图:
顶点v的度是指依附于该顶点的边的条数,记为TD(v)
所有顶点的度之和为边的数量乘以2
对于有向图:
入度是以顶点v为终点的有向边的数目,记为ID(v);
出度是以顶点v为起点的有向边的数目,记为OD(v).
顶点的度等于其入度和初度之和
入度之和和出度之和相等,刚好为弧的条数
顶点与顶点的关系描述:
路径——顶点到顶点之间的一条路径是指顶点序列
回路——第一个顶点和最后一个顶点相同的路径称为回路或环
简单路径——在路径序列中,顶点不重复出现的路径称为简单路径
简单回路——除第一个顶点和最后一个顶点外,其余顶点不重复出现的回路称为简单回路
路径长度——路径上边的数目
点到点的距离——从顶点u出发到顶点v之间的最短路径若存在,则此路径的长度称为从u到v的距离。若从u到v根本不存在路径,则记该距离为无穷。
连通图、强连通图:
无向图中,若从顶点v到顶点w有路径存在,则称v和w是连通的
若任意两个顶点都是连通的,则称图g为连通图,否则为非连通图
(对于n个顶点的无向图g,若g是连通图,则最少有n-1条边)
有向图中,若从顶点v到顶点w和从顶点w到v之间都有路径,则称这两个顶点是强连通的
任意一对顶点都是强连通的,则称此图为强连通图。
(n个顶点最少边数为n条)
子图:若边集和顶点集为另外一个图的子集,则称该图为另一个图的子图
若顶点集为全集,则称该图为另一个图的生成子图
无向图中的极大连通子图称为连通分量
有向图中的极大强连通子图称为有向图的强连通分量
生成树:
在无向图中
连通图的生成树是包含图中全部顶点的一个极小的连通子图
生成森林:
在非连通图中,连通分量的生成树构成了非连通图的生成森林
边的权、带权图:
边的权——在一个图中,每条边都可以标上具有某种含义的数值,该数值称为该边的权值
带权图——边上带有权值的图称为带权图,也称网。
带权路径长度——当图是带权图时,一条路径上所有边的带权之和,称为该路径的带权路径长度
几种特殊形态的图:
无向完全图——无向图中任意两个顶点之间都存在边
有向完全图——有向图中任意两个顶点之间都存在方向相反的两条弧
稀疏图——边很少的图
稠密图——边很多的图
树——不存在回路,且连通的无向图
图的储存:
邻接矩阵法:
#define maxnum 10 //顶点数目的最大值
typedef struct {
char vex[maxnum]; //顶点表
int edge[maxnum][maxnum]; //邻接矩阵,边表
int vexnum, arcnum; //图的当前顶点数和边数/弧数
}mgraph;(用0和1标记两个点之间是否存在边,故有向图和无向图之间不同)
求顶点的度,入度和出度:
(1)在有向图中:
只需检查行或列的1的个数即为度的大小
(2)在无向图中:
第i个结点的出度=第i行非零元素的个数
第i个结点的入度=第i列的非零元素的个数
第i个结点的度=第i行、第i列的非零元素个数之和
储存带权图需要用一个上限值来表示无穷,一般用0来表示指向自己的弧
#define maxnum 100; //顶点数目的最大值
#define INFINITY //宏定义常量“无穷”
typedef char vertextype; //顶点的数据类型
typedef int edgetype; //带权图中边上权值的数据类型
typedef struct {
vertextype vex[maxnum]; //顶点
edgetype edge[maxnum][maxnum]; //边的权
int vexbun, arcnum; //图的当前顶点数和弧数
}mgraph;空间复杂度:O(|v|^2)——只和顶点数相关,和实际的边数无关
适合用于存储稠密图
无向图的邻接矩阵是对称矩阵所以只需存储上三角区或者下三角区进行压缩存储
邻接表法:
//用邻接表存储的图
typedef struct {
adjlist vertices;
int vexnum, arcnum;
}algraph;
//顶点
typedef struct vnode {
vertextype data; //顶点信息
arcnode* first; //第一条边/弧
}vnode,adjlist[maxnum];
//边/弧
typedef struct arcnode {
int adjvex; //边弧指向哪个结点
struct arcnode* next; //指向下一条弧的指针
//Infotype info; //边权值
}arcnode;空间复杂度O(|v|+2|e|);有向图O(|v|+|e|)
计算有向图的度、入度不方便
十字链表法(存储有向图)
(前面学过不是很懂)

邻接多重表(存储无向图)
无向图存储时用邻接表删除一个数据很不方便故用邻接多重表来储存无向图