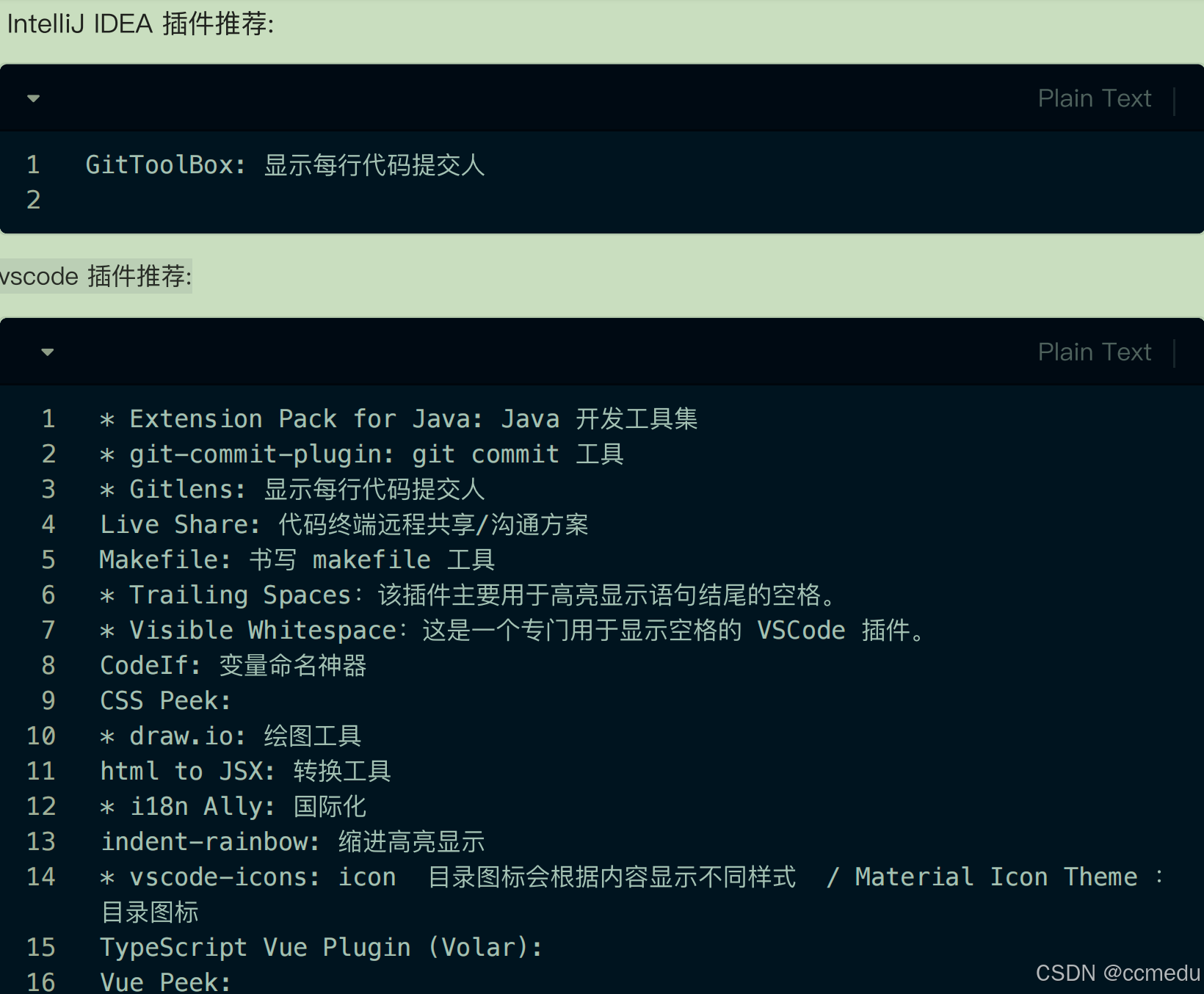
题目链接：P1030 [NOIP2001 普及组] 求先序排列 - 洛谷 | 计算机科学教育新生态

思路：                   

1.先确定跟节点
2.根据根节点，划分出左右子树

中：BADC
后：BDCA

分析：

根据后序遍历，整个序列里最后一个元素，可以看出A是根节点，再来看中序遍历，根据根结点A，我们可以划分出左右两个区域，左子树是B，右子树是DC，再转到后序遍历，也可以划分出左右两个区域，左子树是B，右子树是DC

                                  

根据前序遍历，先输出根结点A，在去处理左子树，可以观察一下左子树的信息和刚开始这棵树的信息是一样的，当分析出左子树信息的时候，我拿到的是他中序遍历的结果和后序遍历的结果，此时划分左右子树发现他只有根节点B，所以直接输出个B就行，此时左子树处理完毕，回到右子树上，在后序遍历里面先确定根结点，输出C，在去中序遍历里面划分区间，左子数是D，右子树是不存在的，所以又划分出来了中序遍历和后序遍历都是D，此时输出D，前序遍历的结果就是ABCD

我们可以发现，无论是哪个区域，我们处理的方法都是一样的，依照后序遍历确定根节点，根据根节点划分出左右子树，所以可以用递归实现整个流程

递归细节：

传参：在题目里面，我们首先拿到的是两个字符串，在第一个问题里面，我们处理的是整个字符串，当递归到左右子树的时候，我们拿的字符串的一部分，因此在传参的时候，你只需告诉我原字符串要处理哪一段就行了，就可以定四个变量，让l1指向中序遍历要处理的左端点，r1指向中序遍历要处理的右端点， l2后序遍历要处理的左端点， r2 后序遍历要处理的右端点

递归处理划分左右子树：假设根节点p落在第三个位置，在中序遍历里要处理的区间是l1到p-1，右子树要处理的区域是p+1到r1，根据中序遍历，我们可以知道左区域的长度，p-1-l1+1=p-l1，所以后序遍历的左区间是l2到l2+p-l1-1，右区间的左端点是l2+p-l1-1+1=l2+p-l1，有端点是r2-1

递归出口：当区间长度是1的时候，r1指针会跑到l1的左边，此时的区间是不合法的，就要递归返回

代码实现：

#include <iostream>
#include <string>
using namespace std;

string a, b;

void dfs(int l1, int r1, int l2, int r2)
{
    // 递归出口
    // 当区间不合法时，返回
    if (l1 > r1) return;

    // 1. 确定根节点 - b[r2]
    cout << b[r2];

    int p = l1;
    while (a[p] != b[r2]) p++; // p 用来标记中序遍历中根节点的位置

    // 2. 划分左右子树
    dfs(l1, p - 1, l2, l2 + p - l1 - 1); // 递归处理左子树
    dfs(p + 1, r1, l2 + p - l1, r2 - 1); // 递归处理右子树
}

int main()
{
    cin >> a >> b;
    dfs(0, a.size() - 1, 0, b.size() - 1);

    return 0;
}