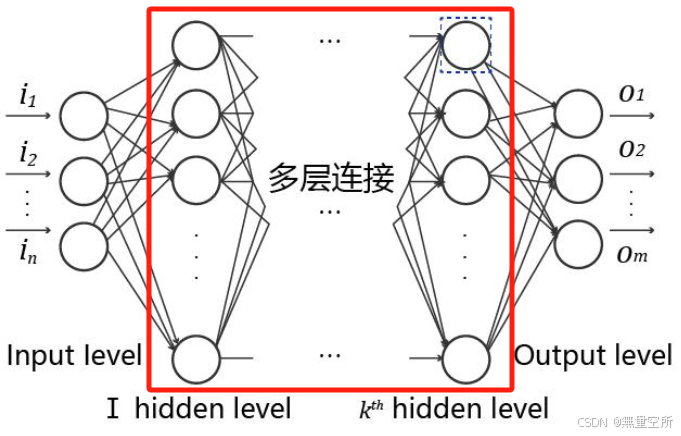
集成学习算法

集成学习算法

一、集成学习介绍

二、随机森林算法

1、Bootstrap随机抽样

2、Bagging 算法

3、训练算法

4、代码实现

三、Boosting 算法

AdaBoost 算法

1、强分类器与弱分类器

2、训练算法

3、代码实现

一、集成学习介绍

集成学习是通过多个模型的组合形成一个精度更高的模型，参与组合的模型称为弱学习器

在预测时使用这些弱学习器模型联合进行预测；训练时需要用训练样本集依次训练出这些弱学习器。

二、随机森林算法

随机森林由多棵决策树组成，因此每一棵决策树就是一个弱学习器。

分类问题：一个测试样本会送到每一棵树中进行预测，然后投票，得票最多的类为最终分类结果。

回归问题：随机森林的预测输出是所有决策树输出的均值。

1、Bootstrap随机抽样

抽样是指从一个样本数据集中随机选取一些样本，形成新的数据集。Bootstrap 使用的是有放回抽样。

做法：在有 n 个样本的集合中有放回地抽取 n 个样本。在这个新的数据集中原始样本集中的一个样本可能会出现多次，也可能不出现。假设样本集中有 n 个样本，每次抽中其中任何一个样本的概率都为 1/n，一个样本在每次抽样中没被抽中的概率为 1-1/n。由于是有放回抽样，每次抽样都是相互独立的，因此，对连续 n 次抽样，一个样本没被抽中的概率为： $(1-1/n)^n$

2、Bagging 算法

在 Bootstrap 抽样的基础上可以构造出 Bagging（Bootstrap Aggregation）算法。

做法：对训练样本集进行多次 Bootstrap 抽样，每次抽样形成的数据集用于训练一个弱学习器模型，得到多个独立的弱学习器，最后用它们的组合进行预测。训练流程如下：

T 为弱学习器的数量

3、训练算法

随机森林对训练样本和特征向量的分量都进行了随机采样。

样本的随机采样（Bootstrap抽样）：

在构建每棵决策树时，随机森林会从原始训练数据集中通过有放回抽样的方式随机选择样本。这意味着某些样本可能被多次选中，而另一些样本可能一次都没有被选中。这种采样方式有助于增加模型的多样性，因为每棵树都是在略有不同的数据集上训练的。
构建方法：用均匀分布的随机数构造，如果有 $l$ 个训练样本，只需要将随机数变换到区间 $[0,l-1]$ 即可。每次抽取样本时生成一个该区间内的随机数，然后选择编号为该随机数的样本。

特征的随机采样：

在构建决策树的每个节点时，随机森林不是使用所有的特征，而是从所有特征中随机选择一部分特征。例如，如果原始数据集有10个特征，随机森林可能会随机选择其中的5个特征来决定最佳分割点。这种随机选择特征的方式有助于减少特征之间的相互影响，防止某些特征在决策过程中占据主导地位，从而提高模型的泛化能力。
对特征分量的采样是无放回抽样，可以用随机洗牌的方式实现。

训练每一棵决策树时都有部分样本未参与训练，可以在训练时利用这些没有被选中的样本做测试，统计它们的预测误差，这称为包外误差。增加决策树的数量，包外误差会下降，因此一种确定决策树数量的思路是通过观察包外误差来决定何时终止训练，当包外误差稳定了之后停止训练。

4、代码实现

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score

# 加载Iris数据集
iris = load_iris()
X = iris.data  # 特征数据
y = iris.target  # 目标值（标签）

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 创建RandomForestClassifier模型
rf_classifier = RandomForestClassifier(n_estimators=5, random_state=42)

# 训练模型
rf_classifier.fit(X_train, y_train)

# 使用测试集进行预测
y_pred = rf_classifier.predict(X_test)

# 计算并打印准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")

三、Boosting 算法

由多个弱学习器组成，预测时用每个弱学习器分别进行预测，然后投票得到结果；

训练时依次训练每个弱学习器，在这里采用了与随机森林不同的策略，不是对样本进行独立的随机抽样构造训练集，而是重点关注被前面的弱分类器错分的样本。

AdaBoost 算法

自适应提升（Adaptive Boosting），是 Boosting 算法的一种实现版本。用于分类问题。用弱分类器的线性组合来构造强分类器。

AdaBoost 算法的核心思想就是关注之前被错分的样本，准确率高的弱分类器有更大的权重。

1、强分类器与弱分类器

强分类器计算公式： $F(x) = \sum_{t=1}^{T} \alpha_t f_t(x)$

x 为输入向量
$F(x)$ 为强分类器
$f_t(x)$ 为弱分类器
$\alpha _t$ 为弱分类器的权重
T 为弱分类器的数量

对于二分类问题，弱分类器的输出值为+1 或-1，分别对应正样本或负样本。分类时的判定规则为： $sgn(F(x))$ 。强分类器的输出值也为+1 或-1，同样对应于正样本或负样本。之所以叫弱分类器是因为它们的精度不用太高，对于二分类问题，只要保证准确率大于 0.5 即可，即比随机猜测强，随机猜测也有 0.5的准确率。

2、训练算法

训练样本的权重值
初始时所有样本的权重相等，在训练过程中，被前面的弱分类器错分的样本会加大权重，反之会减小权重，这样接下来的弱分类器会更加关注这些被错分的样本。
弱分类器的权重值
根据弱分类器的准确率构造，精度越高的弱分类器权重越大。

给定 $l$ 个训练样本 $(x_i,y_i)$ ，其中 $x_i$ 是特征向量， $y_i$ 是类别标签，其值为+1 或-1。训练流程如下：

初始化样本权重值，所有样本的初始权重相等： $w_i^0 = 1 / l, i = 1,2,...,l$

循环，对 $t = 1,2,...,T$ 依次训练每个弱分类器：

        训练一个弱分类器 $f_t(x)$ ，并计算它对训练样本集的错误率 $e_t = \frac{\sum_{i=1}^{t} w_i^t |f_t(x_i) - y_i|}{2 \sum_{i=1}^{l} w_i^{t-1}}$
        计算弱分类器的权重： $\alpha_t = \frac{1}{2} \ln \frac{1 - e_t}{e_t}$
        更新所有样本的权重： $w_i^t = w_i^{t-1} \frac{\exp(-y_i \alpha_t f_t(x_i))}{Z_t}$ （其中， $Z_t$ 为归一化因子，它是所有样本的权重之和： $Z_t = \sum_{i=1}^{l} w_i^{t-1} \exp(-y_i \alpha_t f_t(x_i))$ ）由于被弱分类器正确分类的样本有 $y_if_t(x_i) = +1$ ,被弱分类器错误分类的样本有 $y_if_t(x_i) = -1$ ，如果不考虑归一化因子样本权重更新公式可以简化为 $w_i^t = \begin{cases} e^{-\alpha_t} \times w_i^{t-1}, & \text{if } f_t(x_i) = y_i \\ e^{\alpha_t} \times w_i^{t-1}, & \text{if } f_t(x_i) \neq y_i \end{cases}$ ，其中 $e^{-\alpha_t} = e^{-\frac{1}{2} \ln \frac{1-e_t}{e_t}} = \sqrt{\frac{e_t}{1-e_t}}$ ，故样本权重更新公式可以进一步简化为： $w_i^t = \begin{cases} \sqrt{\frac{e_t}{1-e_t}} \times w_i^{t-1}, & \text{if } f_t(x_i) = y_i \\ \sqrt{\frac{1-e_t}{e_t}} \times w_i^{t-1}, & \text{if } f_t(x_i) \neq y_i \end{cases}$

结束循环

最后得到强分类器： $\operatorname{sgn}(F(x)) = \operatorname{sgn}\left(\sum_{t=1}^{T} \alpha_t f_t(x)\right)$

弱分类器模型可以选择决策树或逻辑回归等。强分类器是弱分类器的线性组合，如果弱分类器是线性函数，无论怎样组合，强分类器依然是线性的，因此，应该选择非线性模型作为弱分类器。

3、代码实现

# 导入必要的库
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.metrics import accuracy_score

# 加载Iris数据集
iris = load_iris()
X = iris.data
y = iris.target

# 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 初始化DecisionTreeClassifier
base_clf = DecisionTreeClassifier(max_depth=1)

# 使用AdaBoostClassifier，设置弱分类器为DecisionTreeClassifier
ada_clf = AdaBoostClassifier(estimator=base_clf, n_estimators=5)

# 训练模型
ada_clf.fit(X_train, y_train)

# 在测试集上进行预测
y_pred = ada_clf.predict(X_test)

# 计算并打印准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")