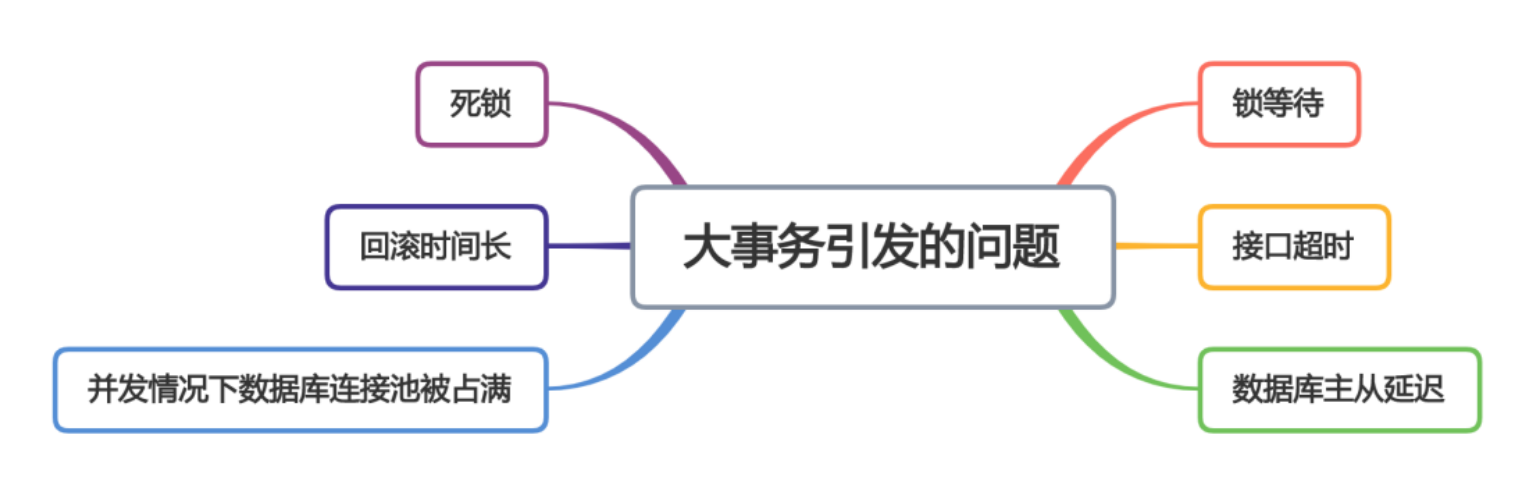
题意：对目标持续施法，法术是每隔y秒让目标开始持续燃烧x秒，每次施法的概率是1/p

求燃烧时间比上总时间的期望值

（题面是laji）

思路：我们把总时间看成许多y段

当x<=y的时候，只有一种情况就是在每y段的0时刻开始烧了x秒

那么他的期望就是res1=1/p*（x/y）

当x>y的时候，对于每y段有两种情况：全燃烧和只有x%y的时间燃烧

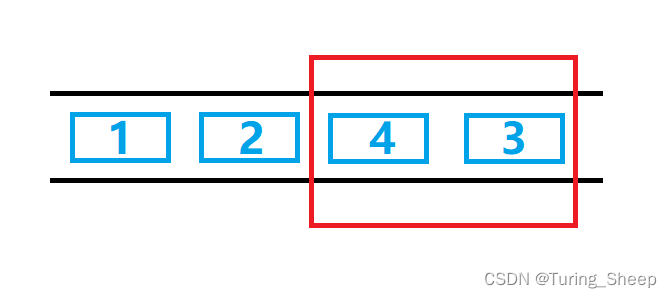
比如一个例子：y=3和x=10

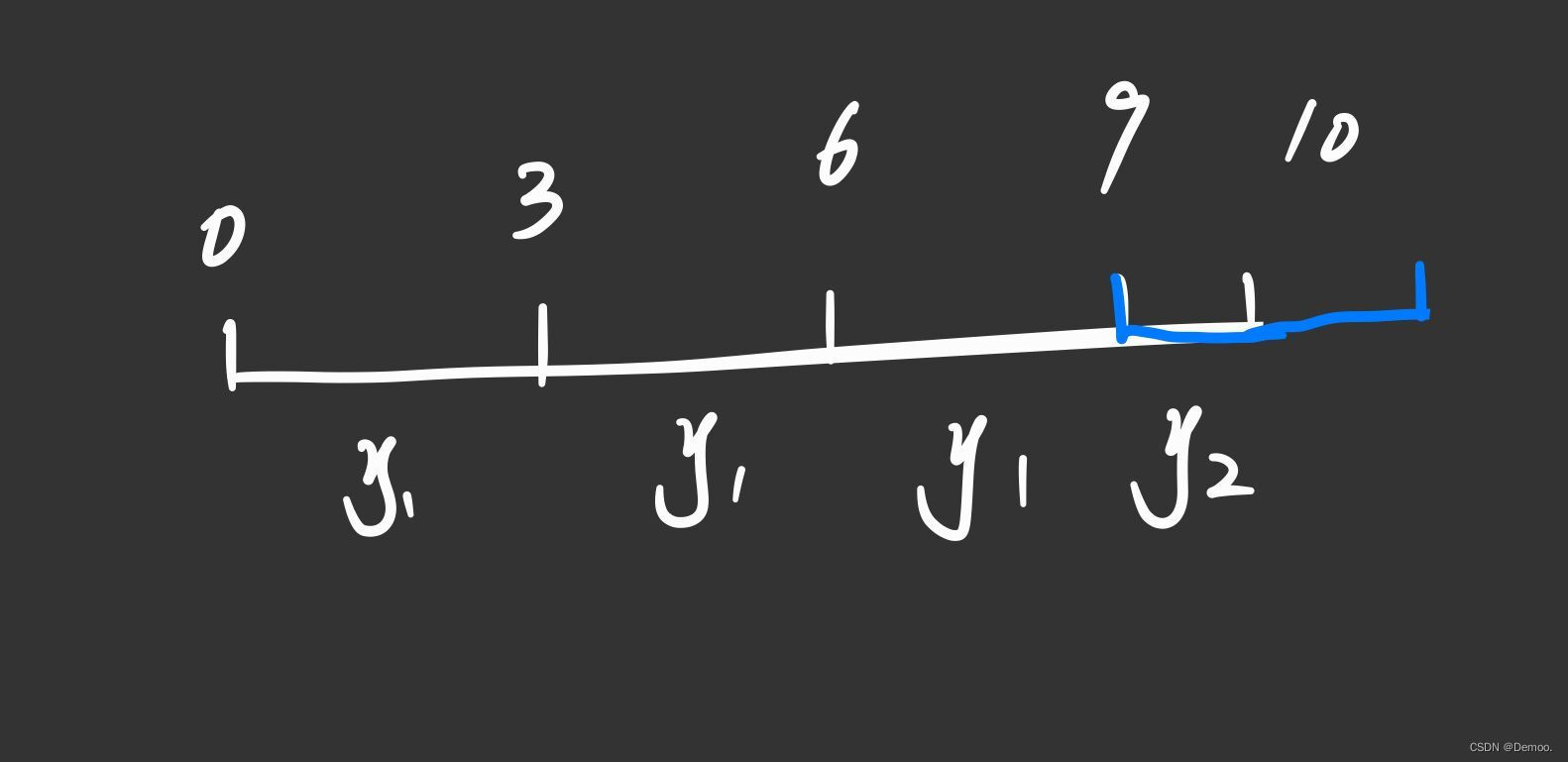
 对于三个y1来说，因为从0时刻燃烧10秒，那么他们的燃烧时间都是y1

都是对于蓝色的y2来说，他的燃烧时间是白色的那段即x%y

那么总共的期望就是这两种的期望的总和

对于y1，因为他在全被燃烧，他可能是第一个y1的情况（在开始的时候燃烧x秒）

也可能是第二种y1的情况（在他的前y秒的时刻点燃x秒）

那么情况就有点复杂，那么我们就算1-与他相反的情况

与他相反的情况是他没有被点燃，

那么从他开始往前数的x秒内的时间内，没有一次被点燃

那么次数就是x/y，没被点燃的概率就是（1-1/p）

那么柿子就是（1-1/p）^(x/y)

要算的是他的相反情况，那么就[1-（1-1/p）^(x/y)]*y

那么该算y2的情况了

对于y2来说，只有在他前面x秒的第一时刻才能点燃，往后的都不点燃才能让y2燃烧（x%y）秒

（比如例子，只有在第0时刻燃烧，第3,6,9时刻都不燃烧，才能让y2燃烧1）

那么他的期望就是1/p*(1-1/p)^(x/y)*(x%y）

那么燃烧时间总的期望res就是：

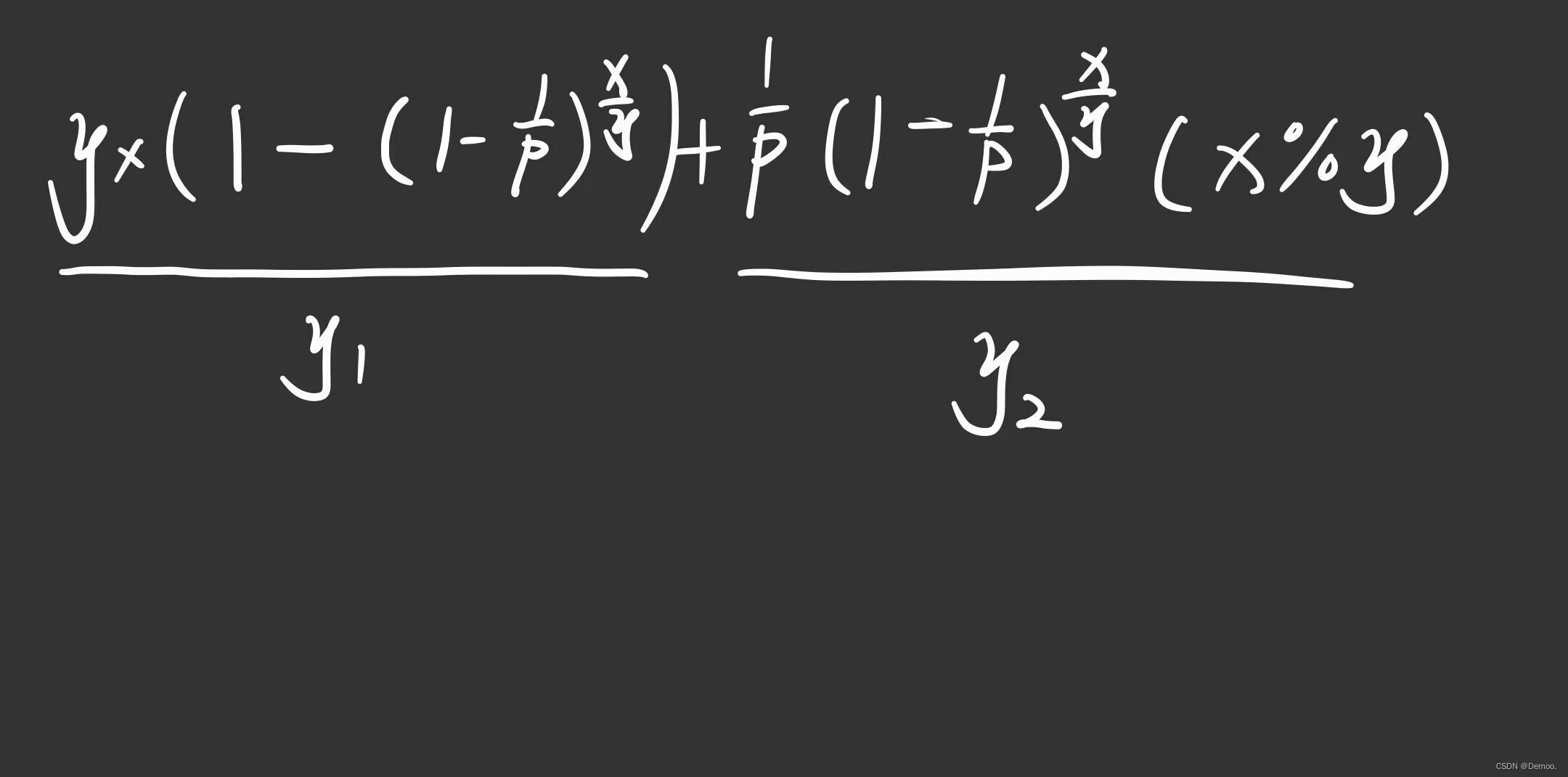
 比上总时间的期望y，就是res/y

	if(x<=y){
		printf("%.15f\n",1.0/p*x/y);
	}else{
		double res1=y*(1-ksm(1-1.0/p,x/y));
		double res2=(x%y)*(1.0/p*ksm(1-1.0/p),x/y);
		printf("%.15f\n",(res1+res2)/y);
	}

（不知道会不会卡精度，gym上还没有上题不知道过不过，但是大致思路就是这样）