1、# use:
- [flutter_launcher_icons:]
每次修改完icon后,都需要执行一遍 dart run flutter_launcher_icons
2、开启混淆并打包apk
flutter build apk --obfuscate --split-debug-info=./out/android/app.android-arm64.symbols
3、开启windows支持
flutter config --enable-windows-desktop
4、打包windows生成安装包
flutter pub add --dev msix
dart run msix:create
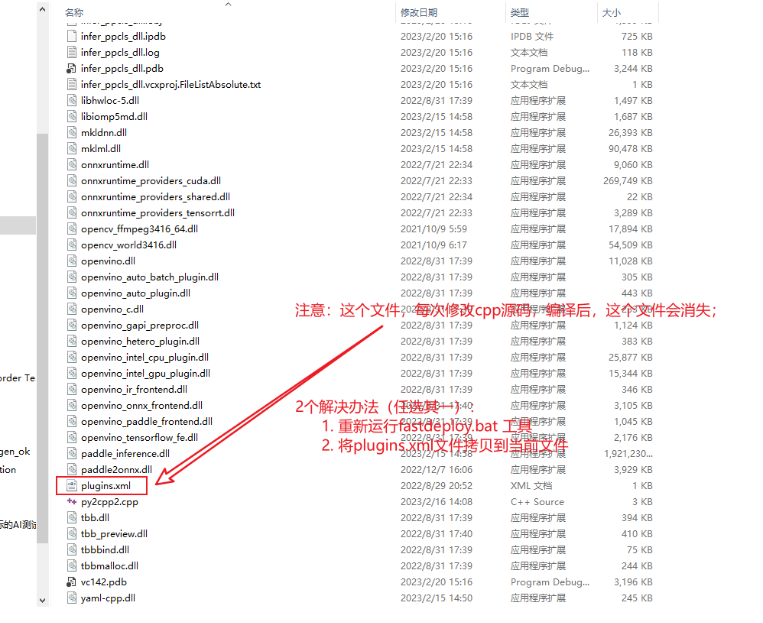
5、windows打包的release版本目录下必须要有SQLite3.dll
重新构建项目的时候要将图像处理dll添加到和SQLite3.dll同目录下
6、添加新的插件需要卸载app重新安装才能生效
7、调用dll时,需要dll是64位
8、在exe程序打开之后,把同目录下的所有dll文件的方法加载进来,所以open dll的时候直接写名字
9、修改windows窗口名字:windows>runner>main.cpp>window.Create
10、开启的gl服务如何关闭?
打开命令提示符:按 Win + R 键,输入 cmd,然后按回车键。
输入netstat -ano | findstr :6688
找到最后一行 pid ,然后打开任务管理器,点击详细信息选项卡,找到对应的pid删除任务即可