股市投资策略升级：掌握马尔可夫决策过程与强化学习，提升交易技能

作者：老余捞鱼

原创不易，转载请标明出处及原作者。

写在前面的话：本文将深入探讨马尔可夫决策过程（MDP）和强化学习在股票交易中的运用。通过阐述MDP的基本原理和其在交易策略中的实际应用，试图向您揭示这些先进技术如何帮助投资者做出更明智的决策。同时我还提供了案例和代码示例，使读者能够更直观地理解这些概念，从而在股票市场中获得优势。

对于那些渴望持续盈利的投资者来说，股票交易无疑是一项既复杂又充满挑战的任务。准确预测股票价格可能被上升到玄学的高度，但如果我们能教会计算机如何做出明智的交易决策呢？这就是马尔可夫决策过程（MDP）和强化学习（RL）的用武之地。

一、什么是马尔可夫决策过程？

马尔可夫决策过程（Markov Decision Process, MDP）是一种用于建模决策问题的数学框架，广泛应用于人工智能、运筹学和经济学等领域。MDP提供了一种系统的方法来描述在不确定环境中进行决策的过程，特别是在状态和行动之间存在随机性的情况下。

尽管市场未来充满了不确定性，但MDP提供了一种策略，能帮助我们在每一步做出最佳选择，以实现长期的投资目标。通过这种方式，投资者可以更科学地规划他们的投资路径，即使面对不确定的市场环境，也能更加自信地做出决策。

1.1 MDP的基本组成部分

马尔可夫决策过程主要由以下几个要素构成：

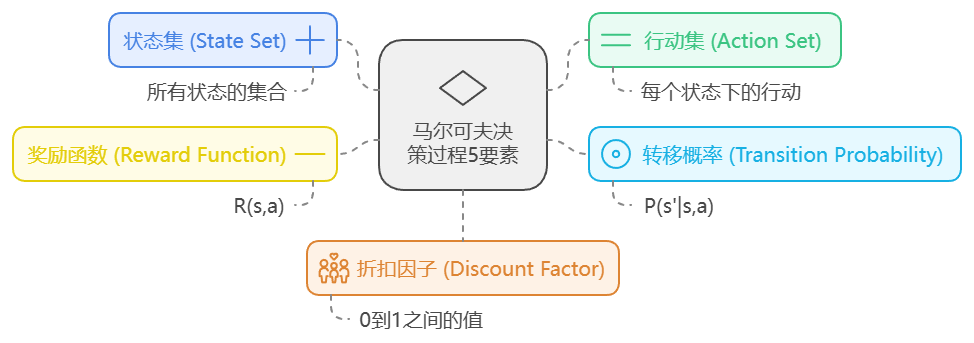
状态集（S）：表示系统可能处于的所有状态的集合，也可理解为当前形势或环境（如某一天的股票价格）。
行动集（A）：表示在每个状态下可以采取的所有可能行动的集合（如买入、卖出或持有）。
转移概率（P）：采取某种行动后，一种状态转变为另一种状态的概率（例如，买入股票后股价上涨的概率）。通常表示为 ( P(s'|s,a) )，其中 ( s ) 是当前状态，( a ) 是采取的行动，( s' ) 是下一个状态。
奖励函数（R）：行动后的直接收益或损失（如出售股票的利润或损失）。通常表示为 ( R(s,a) )，表示在状态 ( s ) 下采取行动 ( a ) 所获得的奖励。
折扣因子（γ）：平衡短期与长期回报的参数。折扣系数越低，代理人就越在乎眼前的回报。

1.2 MDP的决策过程

在MDP中，决策者的目标是选择一个策略（policy），即在每个状态下选择行动的规则，以最大化长期累积奖励。策略可以是确定性的（在每个状态下选择一个特定的行动）或随机的（在每个状态下以一定概率选择不同的行动）。

MDP的核心是马尔可夫性质，即未来状态仅依赖于当前状态和所采取的行动，而与过去的状态无关。这一特性使得MDP能够有效地建模许多实际问题。

在股票交易中，MDP 可以帮助我们模拟交易者如何随着时间的推移与市场价格互动，并做出连续决策，以最大化其投资组合的价值。每天都被视为一个状态，目标是采取正确的行动，使投资组合随着时间的推移不断增长。

1.3 MDP的应用

马尔可夫决策过程在多个领域有着广泛的应用，金融决策是其最最重要的一个领域，其他包括但不限于：

金融决策：用于投资组合优化和风险管理。
医疗决策：辅助医生在治疗方案中做出最佳选择。
游戏AI：用于设计智能体在游戏中做出决策。
机器人导航：帮助机器人在未知环境中做出最佳路径选择。

二、什么是强化学习（RL）？

强化学习（RL）是机器学习的一个分支，其中一个代理通过与环境的交互，在试错中学会做决定。代理根据自己的行为接受奖励或惩罚，并随着时间的推移利用这些奖励或惩罚改进自己的行为。RL 相关流程包括：

代理：决策者（如我们的交易算法）。
环境：股票市场提供价格和回报。
行动：代理人做出的选择（如购买、出售、持有）。
策略：代理遵循的策略，将状态映射为行动。
奖励信号：每次行动后给代理的反馈（如交易的盈亏）。
价值函数：衡量处于特定状态或遵循特定政策的长期回报。

三、MDP 和 RL 如何融入股票交易？

3.1 理念介绍

在股票交易中，交易者需要反复做出决策，而且往往需要掌握不完整的未来信息。这使得 MDP 和 RL 非常适合开发自动交易系统。下面就来看看它们是如何契合的：

状态：每天的市场状况，包括股票价格和趋势（如价格涨跌）。
行动：交易者必须决定买入、卖出或持有。
奖励：奖励是指每次交易赚取的利润或损失。
过渡概率：股票价格遵循不确定的模式--没有人确切知道下一步会发生什么，但 MDP 可以根据现有信息优化决策，从而帮助管理这种不确定性。
行动中的 RL：RL 代理通过反复交易从过去的数据中学习，随着时间的推移不断更新策略，做出更明智的决策。

在股票交易中，代理通过与历史市场数据互动来学习如何交易。随着时间的推移，它将学会在各种市场条件下哪些操作最有利可图。

3.2 基础环境搭建

加载所需的库

#required libraries 
import numpy as np
import matplotlib.pyplot as plt
import yfinance as yf
import pandas as pd
from pykalman import KalmanFilter  # Using pykalman for the Kalman filter

获取数据：我们获取了苹果公司两年的历史数据。我们计算每日回报，并删除所有缺失值。

# Fetch stock data (Apple)
stock = yf.Ticker("AAPL")  
data = stock.history(period="2y")
returns = data['Close'].pct_change().dropna().to_numpy()  # Daily returns

# Save the data to a CSV file for later use
data.to_csv('AAPL_stock_data.csv')  # Save the historical data

参数初始化

N = 504: 共有 504 个交易日，代表系统的状态。
A = 3:可用的三个操作
保持：什么也不做。
卖出：卖出该股票。
买入：买入该股票。
GAMMA = 0.99: 折扣系数，确保未来回报的重要性略低于眼前回报。
TRADING_COST = 0.005:每笔交易的成本为 0.5%（模拟交易费用）。
TEMP = 1.0: 有助于控制决策随机性的参数（对接下来的探索很重要）。

生成模拟股票收益

在现实中，收益是有噪声的，因此我们在真实收益中加入一些随机噪声，以创建代理所看到的收益。

true_returns = np.random.normal(0, 1, N)
observed_returns = true_returns + np.random.normal(0, 0.5, N)

使用卡尔曼滤波器（Kalman Filter）平滑收益率

卡尔曼滤波器帮助我们过滤掉观察到的回报率中的噪音，并估算出基本趋势（平滑状态）。平滑状态有助于我们做出更好的决策。如果观察到的回报率有噪声，平滑值就会告诉我们回报率可能应该是多少。

kf = KalmanFilter( ... )
filtered_state_means, filtered_state_covariances = kf.filter(observed_returns)
smoothed_state_means, smoothed_state_covariances = kf.smooth(observed_returns)

3.3 初始化价值函数和政策概率说明

Value（价值）：这是我们存储每个状态（日）预期价值的地方。可以把它想象成根据以某种方式行动的价值为每一天打分。
policy_probs：该数组存储每个状态（日）下每个操作（买入、卖出、持有）的概率。

值函数迭代

这是一个核心循环，在这个循环中，代理通过反复更新每个状态（日）的值，直到收敛（即变化变得非常小）为止，试图找到最佳策略。

for ite in range(ITEMAX):
    value_old = value.copy()  # Store old value
    value = np.zeros(N)  # Reset value for this iteration

目标是决定哪种操作（买入、卖出或持有）能在 504 天内获得最大回报。

Hold action (Action 0) 保持行动（行动 0）
回报（Reward） = 今日价格 + 未来价值（贴现）

hold_reward = smoothed_price + GAMMA * value_old[ss]

Sell action (Action 1) 卖出行动（行动 1）
奖励（Reward）= 卖出股票（减去成本）+ 未来价值

sell_reward = smoothed_price * (1 - TRADING_COST) + GAMMA * value_old[ss]

Buy action (Action 2) 购买行动（行动 2）
回报（Reward） = 购买股票的成本 + 未来价值

buy_reward = -smoothed_price * (1 + TRADING_COST) + GAMMA * value_old[ss]

每一天代理都会选择价值最高的行动

value[ss] = np.max(val)

Softmax 策略选择

这确保了代理偶尔会进行探索，而不是总是选择最熟悉的。

exp_vals = np.exp(val - np.max(val))
policy_probs[ss] = exp_vals / np.sum(exp_vals)

3.4 代码组合

上述步骤的组合代码如下：

# PARAMETERS
N = 504  # Number of trading days (states)
A = 3  # Number of actions (buy, sell, hold)
GAMMA = 0.99  # Discount factor
TRADING_COST = 0.005  # 0.5% trading cost
TEMP = 1.0  # Temperature parameter for softmax (controls exploration)

# Generate synthetic stock returns as an example
np.random.seed(42)
true_returns = np.random.normal(0, 1, N)  # True returns
observed_returns = true_returns + np.random.normal(0, 0.5, N)  # Noisy observations

# Define the state-space model for Kalman Filter
kf = KalmanFilter(
    transition_matrices=[1],  # State transition
    observation_matrices=[1],  # Observation matrix
    initial_state_mean=0,  # Initial state mean
    initial_state_covariance=1,  # Initial state covariance
    observation_covariance=0.5,  # Observation noise
    transition_covariance=0.1  # Process noise
)

# Use Kalman Filter to estimate the hidden states
filtered_state_means, filtered_state_covariances = kf.filter(observed_returns)
smoothed_state_means, smoothed_state_covariances = kf.smooth(observed_returns)

# Initialize value and policy arrays
value = np.zeros(N)
policy_probs = np.zeros((N, A))  # Store probabilities for each action

# VALUE FUNCTION ITERATION
ITEMAX = 10000  # Maximum iterations
ITETOL = 1e-6  # Tolerance for convergence

for ite in range(ITEMAX):
    value_old = value.copy()  # Keep the previous value for comparison
    value = np.zeros(N)  # Reset the value function

    # Adjust value for actions
    for ss in range(N):
        val = np.zeros(A)  # Value for each action

        # Use smoothed states instead of observed returns
        smoothed_price = smoothed_state_means[ss]

        # Action 0: Hold
        hold_reward = smoothed_price + GAMMA * value_old[ss]
        val[0] = hold_reward

        # Action 1: Sell
        sell_reward = smoothed_price * (1 - trading_cost) + GAMMA * value_old[ss]  # Include potential future value
        val[1] = sell_reward

        # Action 2: Buy
        buy_reward = -smoothed_price * (1 + trading_cost) + GAMMA * value_old[ss]  # Cost + potential future value
        val[2] = buy_reward

        # Update value for the current state
        value[ss] = np.max(val)

        # Softmax policy selection
        max_val = np.max(val)
        exp_vals = np.exp(val - max_val)  # Subtract max_val before applying exp
        policy_probs[ss] = exp_vals / np.sum(exp_vals) if np.sum(exp_vals) > 0 else np.zeros(A)


# PLOT THE SMOOTHED RETURNS, VALUE FUNCTION, AND OPTIMAL POLICY PROBABILITIES
plt.figure(figsize=(16, 6))

plt.subplot(1, 3, 1)
plt.plot(smoothed_state_means, label="Smoothed Returns")
plt.title("Smoothed Returns", fontsize="x-large")
plt.xlabel("Days", fontsize="x-large")
plt.legend()

plt.subplot(1, 3, 2)
plt.plot(value, label="Optimized Value Function")
plt.title("Value Function", fontsize="x-large")
plt.xlabel("Days", fontsize="x-large")
plt.legend()

plt.subplot(1, 3, 3)
for action in range(A):
    plt.plot(policy_probs[:, action], marker='o', label=f"Action {action} Probabilities")
plt.title("Optimal Policy Probabilities", fontsize="x-large")
plt.xlabel("Days", fontsize="x-large")
plt.legend()

plt.tight_layout()
plt.show()

3.5 结果分析

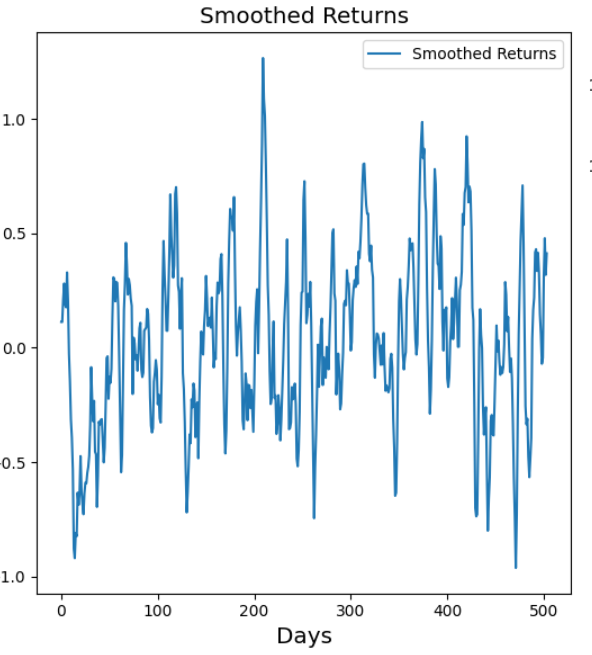
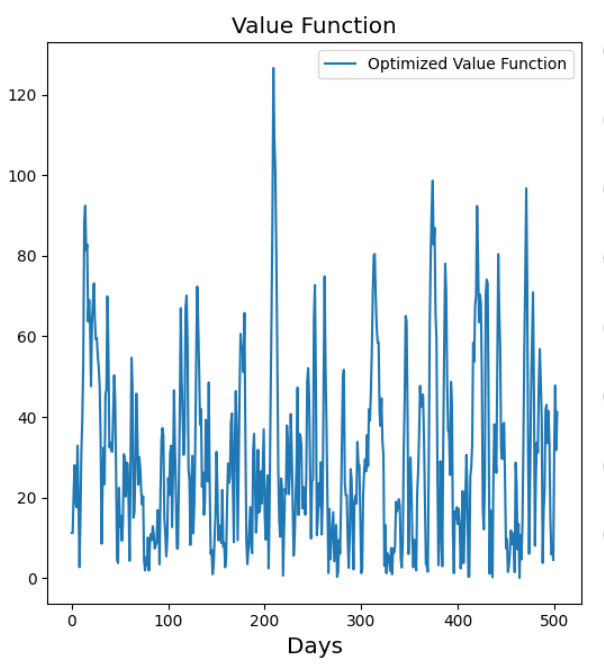
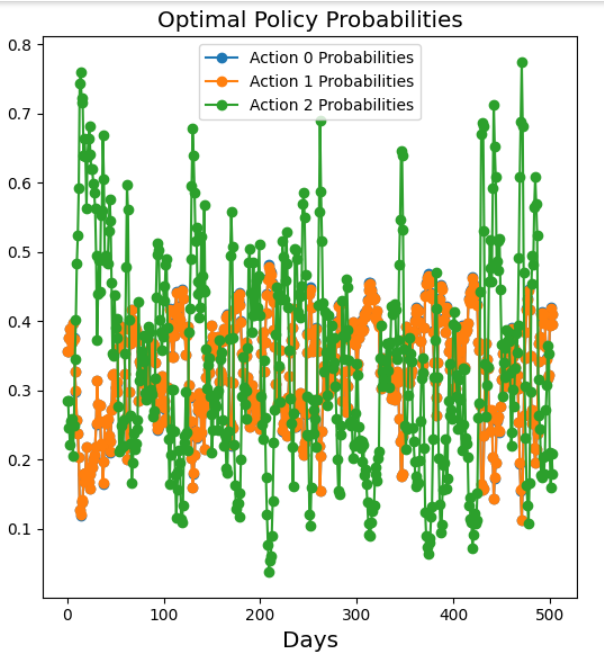
最后，我们将从 10000 美元的投资组合开始，对所采取的行动和投资组合价值进行可视化。根据结果，投资组合的资金增长到 10450 美元。如下图：

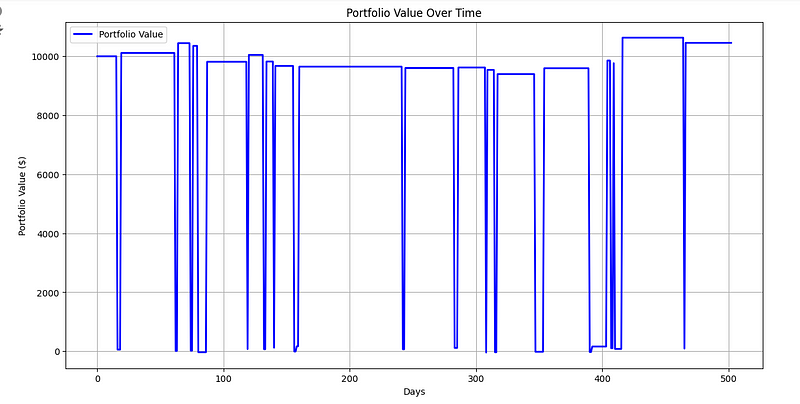
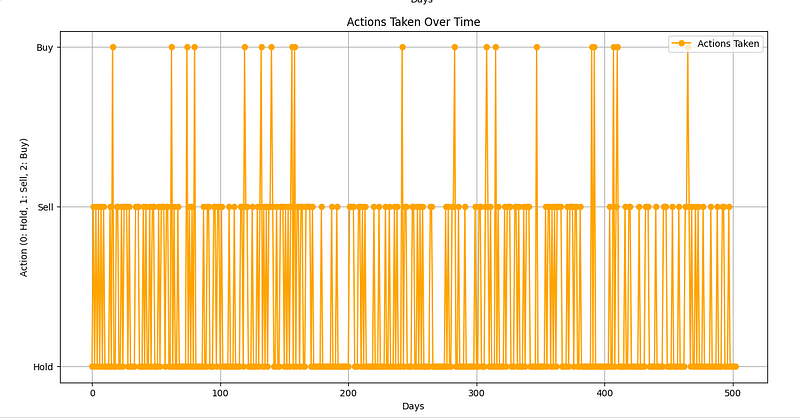
请注意，我们还可以通过 Q-learning 来强化这些结果。

我们的实验结果表明，结合MDP和RL的方法确实可以应用于股票交易，帮助投资者做出更为明智的决策，从而实现收益的最大化。这种方法不仅考虑了市场的动态变化，还能够根据历史数据和当前市场状况，为投资者提供个性化的交易建议。通过这种方式，投资者可以更加科学地管理他们的投资组合，提高投资回报率，并在充满变数的股票市场中保持竞争力。

四、观点总结

在探索如何利用马尔可夫决策过程（MDP）和强化学习（RL）来辅助股票交易决策的过程中，我们采取了一系列措施来提高决策的准确性和效率。首先，我们利用卡尔曼滤波器对股票数据进行处理，这种方法能够过滤掉数据中的噪声，从而更清晰地揭示出真实的趋势。接下来，我们通过模拟不同的操作（如买入、卖出、持有）来训练智能代理，同时考虑到交易成本和预期的未来回报。